Unit identitas atau matriks

Di halaman ini, Anda akan melihat apa itu matriks Identitas (atau Unit) serta beberapa contohnya. Selanjutnya kami jelaskan apa saja sifat-sifat matriks identitas, cara kerja matriks jenis tersebut dan apa hasil determinannya. Terakhir, Anda akan menemukan penerapan yang dimiliki matriks khusus ini.

Apa yang dimaksud dengan matriks identitas?

Matriks Identitas (atau Satuan) adalah matriks persegi yang diisi angka nol (0) kecuali pada diagonal utama yang semua elemennya bernilai satu (1).

Demikianlah pengertian matriks identitas atau matriks kesatuan, namun Anda pasti akan melihatnya lebih jelas melalui contoh:

Contoh matriks identitas

Contoh matriks identitas berdimensi 2×2

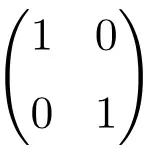
identitas unik atau matriks berdimensi 2x2

Contoh matriks Identitas orde 3×3

identitas atau matriks unik berdimensi 3x3

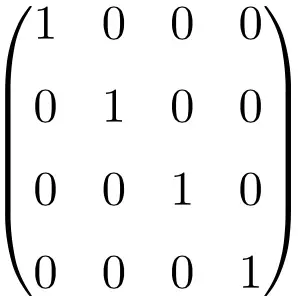
Contoh matriks Identitas ukuran 4×4

identitas atau matriks unik berdimensi 4x4

Seperti yang Anda lihat, untuk membuat matriks identitas kita masih perlu mengikuti prosedur yang sama: letakkan satu (1) pada diagonal utama dan sisanya nol (0). Satu-satunya hal yang berubah adalah ukuran meja.

Properti tabel identitas

Matriks identitas, matriks satuan atau bahkan matriks identik banyak digunakan dalam matematika, hal ini disebabkan oleh ciri-ciri yang dimiliki oleh matriks jenis ini:

Matriks identitas merupakan contoh matriks diagonal .

Matriks kesatuan adalah matriks segitiga atas dan bawah.

Matriks identitas juga merupakan matriks simetris .

Wakil dari matriks identitas itu sendiri.

$\displaystyle \text{Adj}(I) =\begin{pmatrix} 1&0&0\\[1.1ex] 0&1&0 \\[1.1ex] 0&0&1 \end{pmatrix}$

Ini adalah matriks yang dapat dibalik. Dan untuk adjointnya, invers dari matriks Satuan itu sendiri adalah:

$\displaystyle I^{-1}=\begin{pmatrix} 1&0&0\\[1.1ex] 0&1&0 \\[1.1ex] 0&0&1 \end{pmatrix}$

Matriks skalar apa pun dapat diperoleh dari perkalian suatu bilangan dengan matriks identitas:

$\displaystyle 3\cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & 3 \end{pmatrix}$

Semua nilai eigen (atau nilai eigen) dari matriks Identik adalah 1:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} \longrightarrow \ \lambda = 1 \ ; \ \lambda = 1 \ ; \ \lambda = 1$

Terakhir, matriks identitas juga merupakan contoh matriks permutasi .

Operasi dengan matriks Identitas (atau Unit).

Anda mungkin berpikir: semua ini sangat bagus tapi… dan untuk apa matriks Identitas? Kalau saja itu adalah tabel dengan 0 dan 1!

Meskipun Anda mungkin belum pernah membahas topik ini, matriks identitas banyak digunakan dalam matematika, sebenarnya matriks persegi jenis ini sangat penting dalam aljabar linier. Kegunaan utama matriks identitas adalah kemudahannya dalam menghitung operasi matriks. Jadi mari kita lihat cara bekerja dengan matriks Identitas:

Penjumlahan dan Pengurangan dengan Matriks Identitas

Salah satu cara untuk menjumlahkan (atau mengurangi) bilangan-bilangan pada diagonal utama suatu matriks tanpa mengubah unsur-unsur lainnya adalah dengan menggunakan matriks identitas, karena matriks identitas hanya menjumlahkan (atau mengurangkan) satu satuan pada bilangan-bilangan tersebut. elemen:

$\displaystyle \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & 0 & 5 \\[1.1ex] 9 & 6 & -7 \end{pmatrix}+\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 4 & 4 & -1 \\[1.1ex] -2 & 1 & 5 \\[1.1ex] 9 & 6 & -6 \end{pmatrix}$

$\displaystyle \begin{pmatrix} 1 & 7 & 4 \\[1.1ex] 8 & -2 & 3 \\[1.1ex] 0 & 5 & 9 \end{pmatrix}-\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 0 & 7 & 4 \\[1.1ex] 8 & -3 & 3 \\[1.1ex] 0 & 5 & 8 \end{pmatrix}$

Anda juga dapat menambah atau mengurangi lebih banyak satuan pada elemen diagonal dengan terlebih dahulu mengalikan matriks identitas dengan skalar:

$\displaystyle \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & 0 & 5 \\[1.1ex] 9 & 6 & -7 \end{pmatrix}+5\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 8 & 4 & -1 \\[1.1ex] -2 & 5 & 5 \\[1.1ex] 9 & 6 & -2 \end{pmatrix}$

$\displaystyle \begin{pmatrix} 1 & 7 & 4 \\[1.1ex] 8 & -2 & 3 \\[1.1ex] 0 & 5 & 9 \end{pmatrix}-4\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} -3 & 7 & 4 \\[1.1ex] 8 & -6 & 3 \\[1.1ex] 0 & 5 & 5 \end{pmatrix}$

Perkalian suatu matriks dengan matriks identitas

Saat mengalikan suatu matriks dengan matriks identitas, ia bertindak sebagai elemen netral , yaitu matriks apa pun yang dikalikan dengan matriks identitas akan menghasilkan matriks yang sama. Lihatlah contoh berikut:

$\displaystyle \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}\cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}$

Selanjutnya arti perkalian matriks tidak relevan, atau dengan kata lain tidak menjadi masalah apakah matriks identitas kita kalikan ke kanan atau ke kiri karena hasilnya akan selalu matriks yang sama. Untuk mendemonstrasikannya, kita ulangi latihan sebelumnya tetapi kali ini mengalikan matriks Identitas dengan sisi yang berlawanan:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\cdot \displaystyle \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix} = \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}$

Kekuatan matriks identitas

Pangkat matriks identitas selalu menghasilkan matriks identitas, berapa pun eksponen matriks yang kita naikkan dan dimensi matriksnya.

$\left.\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\right. ^2 =\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\left.\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}\right. ^3 =\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

$\left.\begin{pmatrix} 1 & 0 & 0 & 0\\[1.1ex] 0 & 1 & 0 & 0\\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0& 0 &0&1\end{pmatrix}\right. ^5 =\begin{pmatrix} 1 & 0 & 0 & 0\\[1.1ex] 0 & 1 & 0 & 0\\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0& 0 &0&1\end{pmatrix}$

$\left.\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\right. ^n =\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Penentu matriks identitas

Seperti yang saya asumsikan sudah Anda bayangkan, determinan matriks Identitas (atau Unit) selalu sama dengan 1 , berapa pun dimensi matriksnya.

$\displaystyle\begin{vmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{vmatrix} = \bm{1}$

$\displaystyle\begin{vmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{vmatrix}=\bm{1}$

$\displaystyle\begin{vmatrix} 1 & 0 & 0 & 0 \\[1.1ex] 0 & 1 & 0 & 0 \\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0 & 0 & 0 & 1 \end{vmatrix}=\bm{1}$

Aplikasi Matriks Identitas

Terakhir, setelah semua informasi ini, Anda mungkin sudah mengetahui cara menjawab pertanyaan umum mengapa matriks identitas begitu penting? Tenang, saya juga pernah menanyakan pertanyaan ini pada diri saya sendiri. 😂

Seperti yang telah Anda ketahui, matriks identitas memiliki banyak kegunaan dan itulah mengapa matriks ini sangat menarik. Salah satu kegunaan matriks Satuan adalah operasi, karena seperti yang telah kita lihat, sangat mudah untuk melakukan operasi matriks dengannya.

Di sisi lain, matriks identitas juga digunakan untuk menyelesaikan persamaan matriks . Untuk melakukannya, kita menggunakan sifat invers matriks berikut: mengalikan suatu matriks dengan matriks inversnya sama dengan matriks identitas. Anda dapat melihat cara menyelesaikan persamaan dengan matriks dengan mengklik link.

Selain itu, matriks identitas juga digunakan untuk menghitung matriks invers dengan metode Gaussian. Metode ini melibatkan penempatan matriks di sebelah matriks identitas, sehingga membentuk matriks yang lebih besar. Kemudian, matriks asli harus diubah menjadi matriks identitas dengan menerapkan operasi dasar pada barisnya. Kelihatannya ribet banget tapi kenyataannya tidak banyak, namun harus diterapkan seluruh prosedur, jadi jika lebih tertarik bisa mencari cara membalikkan matriks di mesin pencari halaman web (atas ke KANAN).

Terakhir, matriks Identitas juga berguna untuk mendiagonalisasi suatu matriks dan menghitung nilai eigen (atau nilai eigennya). Karena melalui operasi tertentu yang mengintervensi matriks satuan, polinomial karakteristik yang menjadi sumber nilai eigen dapat diperoleh. Tapi ini sudah merupakan subjek yang sangat maju, itulah sebabnya kami memiliki halaman super komprehensif yang didedikasikan untuk diagonalisasi matriks dengan contoh dan latihan yang menjelaskannya. Jika Anda lebih tertarik, Anda dapat mencari panduan ini di mesin pencari kami (kanan atas).

Identitas atau unit matriks