▷ Turunan dari garis singgung (rumus dan latihan yang diselesaikan)

Di sini Anda akan mengetahui bagaimana fungsi tangen diturunkan. Selain itu, Anda akan dapat melihat contoh turunan garis singgung dan bahkan berlatih dengan latihan yang diselesaikan langkah demi langkah. Terakhir, kami juga mendemonstrasikan rumus turunan tangen dan menunjukkan rumus turunan tangen invers.

Apa turunan dari garis singgung?

Turunan garis singgung x sama dengan 1 pada kuadrat kosinus x. Turunan garis singgung x juga setara dengan kuadrat garis potong x, dan 1 ditambah kuadrat garis singgung x.

$\begin{array}{c}f(x)=\text{tan}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{1}{\text{cos}^2(x)}=\text{sec}^2(x)=1+\text{tan}^2(x)\end{array}$

Semua ekspresi adalah ekuivalen, sehingga fungsi tangen memiliki tiga kemungkinan rumus untuk menurunkannya.

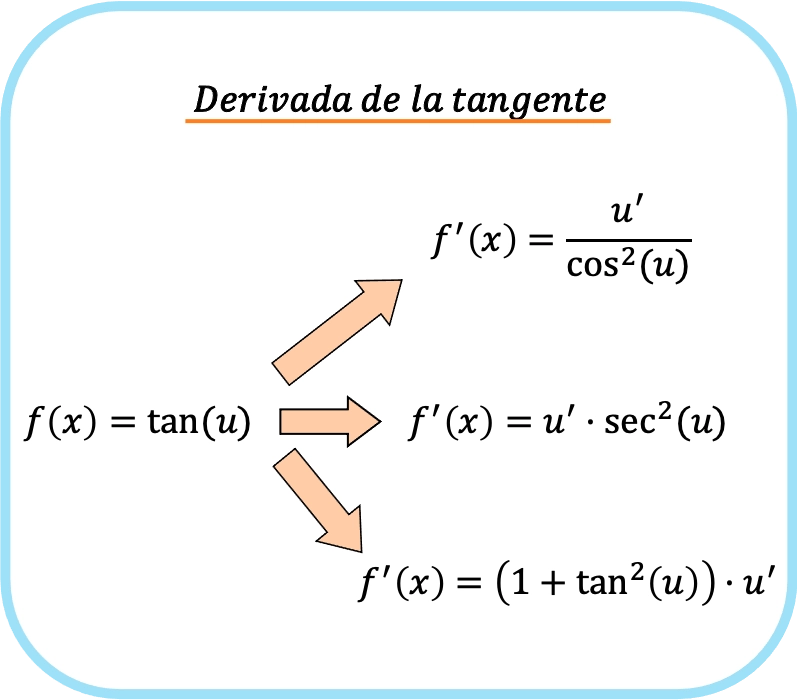
Di sisi lain, jika dalam argumen tangen kita mempunyai fungsi yang berbeda dari x (sebut saja u), kita harus menerapkan aturan rantai. Oleh karena itu, turunan dari garis singgung u adalah:

$\begin{array}{c}f(x)=\text{tan}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{u'}{\text{cos}^2(u)}=\text{sec}^2(u)\cdot u'=\left(1+\text{tan}^2(u)\right)\cdot u'\end{array}$

Singkatnya, aturan turunan tangen dapat diringkas sebagai berikut:

Contoh turunan tangen

Mengingat rumus turunan tangen, pada bagian ini kita akan menyelesaikan beberapa contoh turunan trigonometri jenis ini agar Anda memahami cara menurunkan fungsi tangen.

Contoh 1: Turunan dari garis singgung 2x

$f(x)=\text{tan}(2x)$

Untuk menghitung turunan garis singgung, Anda dapat menggunakan salah satu dari tiga rumus yang kita lihat di atas. Dalam hal ini, kita akan menggunakan rumus cosinus:

$f(x)=\text{tan}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cos}^2(u)}$

Fungsi 2x linier maka turunannya adalah 2. Jadi turunan garis singgung 2x adalah 2 terhadap kuadrat kosinus 2x:

$f(x)=\text{tan}(2x)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2}{\text{cos}^2(2x)}$

Contoh 2: Turunan dari garis singgung x kuadrat

$f(x)=\text{tan}(x^2)$

Dalam contoh ini, argumen tangen fungsi bukanlah x, melainkan fungsi dengan turunan. Artinya kita perlu menerapkan aturan rantai untuk menurunkannya.

$f(x)=\text{tan}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cos}^2(u)}$

Turunan x kuadrat adalah 2x, maka turunan garis singgung x ² adalah:

$f(x)=\text{tan}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2x}{\text{cos}^2(x^2)}$

Contoh 3: Turunan dari garis singgung kubus

$f(x)=\text{tan}^3(9x^2-4x)$

Dalam soal ini kita mempunyai fungsi komposit, jadi kita juga perlu menggunakan aturan rantai untuk membedakan garis singgung.

$f(x)=\text{tan}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cos}^2(u)}$

Selain itu, tangen dipangkatkan 3, artinya sebelum menerapkan rumus turunan tangen harus menggunakan rumus turunan suatu pangkat:

$\begin{aligned}f'(x)&=3\text{tan}^2(9x^2-4x)\cdot \cfrac{18x-4}{\text{cos}^2(9x^2-4x)} \\[2ex]&=\cfrac{3\text{tan}^2(9x^2-4x)\cdot(18x-4)}{\text{cos}^2(9x^2-4x)}\end{aligned}$

Turunan dari garis singgung terbalik

Seperti fungsi invers lainnya, fungsi tangen juga mempunyai invers, yaitu fungsi tangen busur. Meskipun rumus untuk menurunkannya tidak mirip dengan rumus tangen, kami tunjukkan kepada Anda karena dapat berguna dalam beberapa kasus.

Turunan invers tangen suatu fungsi adalah hasil bagi turunan fungsi tersebut dibagi satu ditambah kuadrat fungsi tersebut.

$f(x)=\text{tan}^{-1}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1+u^2}$

Misalnya turunan invers tangen 3x adalah:

$f(x)=\text{tan}^{-1}(3x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{3}{1+(3x)^2}=\cfrac{3}{1+9x^2}$

Latihan soal turunan garis singgung

Hitung turunan fungsi tangen berikut:

$\text{A) } f(x)=\text{tan}(3x)$

$\text{B) } f(x)=\text{tan}(x^3-10x^2+8)$

$\text{C) } \displaystyle f(x)=\text{tan}^2\left(\frac{x}{2}\right)$

$\text{D) } f(x)=\text{tan}\left(e^{2x}\right)$

$\text{E) } f(x)=\text{tan}\bigl(\ln(4x)\bigr)$

$\text{F) } f(x)=\text{tan}\left(\sqrt{3x}\right)$

Lihat solusinya

$\text{A) } f'(x)=\cfrac{3}{\text{cos}^2(3x)}$

$\text{B) } f'(x)=\cfrac{3x^2-20x}{\text{cos}^2(x^3-10x^2+8)}$

$\text{C) } \displaystyle f'(x)=2\text{tan}\left(\frac{x}{2}\right)\cdot \frac{1}{\text{cos}^2\left(\frac{x}{2}\right)}\cdot \frac{1}{2}=\frac{\text{tan}\left(\frac{x}{2}\right)}{\text{cos}^2\left(\frac{x}{2}\right)}$

$\text{D) } f'(x)=\cfrac{2e^{2x}}{\text{cos}^2(e^{2x})}$

$\text{E) } f'(x)=\cfrac{\frac{4}{4x}}{\text{cos}^2\bigl(\ln(4x)\bigr)}=\cfrac{1}{x\cdot\text{cos}^2\bigl(\ln(4x)\bigr)}$

$\text{F) } f'(x)=\cfrac{\frac{3}{2\sqrt{3x}}}{\text{cos}^2\left(\sqrt{3x}\right)}=\cfrac{3}{2\sqrt{3x}\cdot \text{cos}^2\left(\sqrt{3x}\right)}$

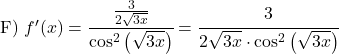
Bukti turunan garis singgung

Agar Anda dapat memverifikasi bahwa ini bukan ekspresi yang dibuat-buat, di bagian ini kami akan mendemonstrasikan rumus turunan tangen menggunakan definisi matematis tangen.

Untuk melakukannya, kita akan mulai dari identitas trigonometri yang menghubungkan ketiga perbandingan trigonometri:

$\text{tan}(x)=\cfrac{\text{sen}(x)}{\text{cos}(x)}$

Jika kita menggunakan rumus turunan suatu pembagian , maka turunannya adalah:

$\displaystyle\left(\text{tan}(x)\right)'=\left(\frac{\text{sen}(x)}{\text{cos}(x)}\right)'$

$\text{tan}'(x)=\cfrac{\text{cos}(x)\cdot \text{cos}(x)+\text{sen}(x)\text{sen}(x) }{\text{cos}^2(x)}$

$\text{tan}'(x)=\cfrac{\text{cos}^2(x)+\text{sen}^2(x)}{\text{cos}^2(x)}$

Namun, dengan menggunakan identitas trigonometri dasar, kita mengetahui bahwa kuadrat sinus ditambah kuadrat kosinus adalah 1:

$\text{sen}^2(x)+\text{cos}^2(x)=1$

$\text{tan}'(x)=\cfrac{1}{\text{cos}^2(x)}$

Jadi kita telah sampai pada rumus pertama turunan garis singgung. Selain itu, garis potong adalah kebalikan perkalian dari kosinus, sehingga ekspresi kedua juga diturunkan:

$\text{tan}'(x)=\text{sec}^2(x)$

Terakhir, aturan ketiga turunan tangen dapat dibuktikan dengan mengubah pecahan dari langkah sebelumnya menjadi penjumlahan pecahan:

$\text{tan}'(x)=\cfrac{\text{cos}^2(x)+\text{sen}^2(x)}{\text{cos}^2(x)}$

$\text{tan}'(x)=\cfrac{\text{cos}^2(x)}{\text{cos}^2(x)}+\cfrac{\text{sen}^2(x)}{\text{cos}^2(x)}$

$\text{tan}'(x)=1+\text{tan}^2(x)$

Apa turunan dari garis singgung?

Contoh turunan tangen

Contoh 1: Turunan dari garis singgung 2x

Contoh 2: Turunan dari garis singgung x kuadrat

Contoh 3: Turunan dari garis singgung kubus

Turunan dari garis singgung terbalik

Latihan soal turunan garis singgung

Bukti turunan garis singgung

Tinggalkan Komentar Batalkan Balasan