Di halaman ini Anda akan melihat apa itu aturan Cramer dan, sebagai tambahan, Anda akan menemukan contoh dan latihan penyelesaian sistem persamaan menggunakan aturan Cramer.
Apa aturan Cramer?
Aturan Cramer adalah metode yang digunakan untuk menyelesaikan sistem persamaan dengan determinan. Mari kita lihat cara penggunaannya:
Pertimbangkan sistem persamaan:
![Rendered by QuickLaTeX.com \begin{cases} ax+by+cz= \color{red}\bm{j} \\[1.5ex] dx+ey+fz=\color{red}\bm{k} \\[1.5ex] gx+hy+iz = \color{red}\bm{l} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e0141f3451719f665ef28e4061489551_l3.png)
Matriks A dan matriks perluasan A’ dari sistem tersebut adalah:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} a & b & c \\[1.1ex] d & e & f \\[1.1ex] g & h & i \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} a & b & c & \color{red}\bm{j} \\[1.1ex] d & e & f & \color{red}\bm{k} \\[1.1ex] g & h & i & \color{red}\bm{l} \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1d628a13ec7de4b3ba7a301c0a5d8ac6_l3.png)
Aturan Cramer mengatakan bahwa solusi suatu sistem persamaan adalah:
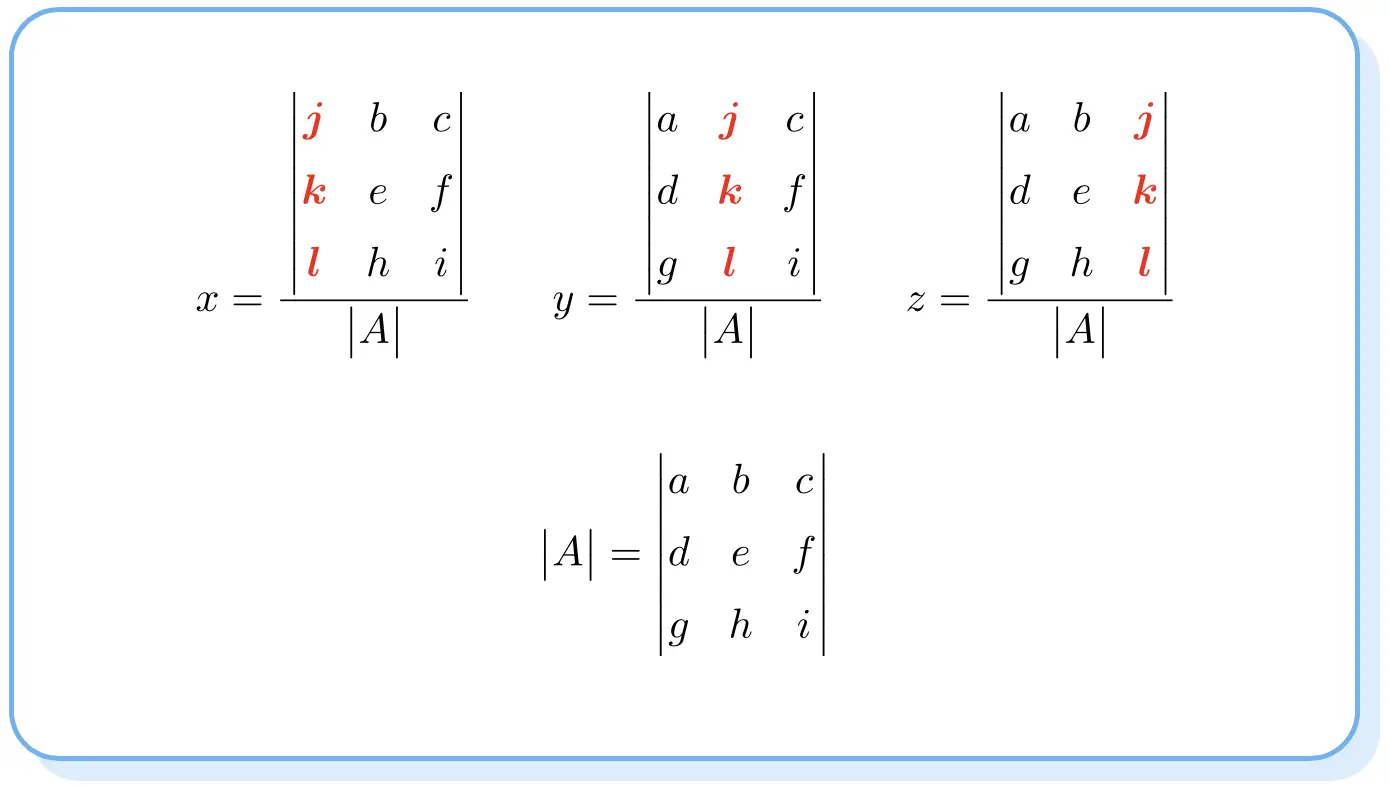
Perhatikan bahwa determinan pembilangnya seperti determinan matriks A tetapi mengubah kolom masing-masing suku yang tidak diketahui menjadi kolom suku-suku bebas.
Oleh karena itu, aturan Cramer digunakan untuk menyelesaikan sistem persamaan linier. Namun seperti yang telah anda ketahui, ada banyak cara untuk menyelesaikan suatu sistem persamaan, misalnyametode Gauss Jordan yang terkenal.
Di bawah ini adalah contoh penyelesaian sistem persamaan linear dengan aturan Cramer, atau terkadang juga ditulis dengan aturan Kramer.
Contoh 1: sistem kompatibel yang ditentukan (SCD)
- Selesaikan sistem 3 persamaan berikut dengan 3 variabel yang tidak diketahui menggunakan aturan Cramer:
![Rendered by QuickLaTeX.com \begin{cases} 2x+y+3z= 1 \\[1.5ex] 3x-2y-z=0 \\[1.5ex] x+3y+2z = 5\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6013b7e73c89c24fe388f1a5d018f32b_l3.png)
Pertama-tama kita buat matriks A dan matriks perluasan A’ dari sistem:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & 3 & 1 \\[1.1ex] 3 & -2 & -1 & 0 \\[1.1ex] 1 & 3 & 2 & 5 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c710ed86223f47f39b5a25720b5ca19d_l3.png)
Sekarang kita menghitung rank kedua matriks tersebut, untuk melihat jenis sistemnya. Untuk menghitung rank A, kita menghitung determinan 3×3 dari seluruh matriks (menggunakan aturan Sarrus) dan melihat apakah hasilnya 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{vmatrix} =-8-1+27+6+6-6 = 24 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-ae4a3bb88d113494463df8e670c326c6_l3.png)
Penentu A berbeda dengan 0, sehingga matriks A mempunyai rangking 3.
![]()
Jadi matriks A’ juga mempunyai rangking 3 , karena matriks tersebut tidak boleh mempunyai rangking 4 dan paling sedikit harus mempunyai rangking yang sama dengan matriks A.
![]()
Luas matriks A sama dengan luas matriks A’ dan jumlah sistem yang tidak diketahui (3), oleh karena itu, berdasarkan teorema Rouché-Frobenius , kita mengetahui bahwa ini adalah sistem kompatibel yang ditentukan (SCD):
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-557185e16670c72d23eec5a3ea13b487_l3.png)
Setelah kami mengetahui bahwa sistem tersebut adalah SCD, kami menerapkan aturan Cramer untuk menyelesaikannya. Untuk melakukannya, ingatlah bahwa matriks A, determinannya, dan matriks A’ adalah:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & 3 & \color{red}\bm{1} \\[1.1ex] 3 & -2 & -1 & \color{red}\bm{0} \\[1.1ex] 1 & 3 & 2 & \color{red}\bm{5} \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-31b2b3e5865c2264c360fb887d37a5f6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{vmatrix} =24](https://mathority.org/wp-content/ql-cache/quicklatex.com-0a604d8f5a3927a47a264d28f7a007b2_l3.png)
Untuk menghitung hal yang tidak diketahui
![]()
Dengan aturan Cramer, kita ubah kolom pertama determinan A dengan kolom suku bebas dan membaginya dengan determinan A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} \color{red}\bm{1} & 1 & 3 \\[1.1ex] \color{red}\bm{0} & -2 & -1 \\[1.1ex] \color{red}\bm{5} & 3 & 2 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{24}{24} = \bm{1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a1fa494ffb5e452d59c4d2dad40f925a_l3.png)
Untuk menghitung hal yang tidak diketahui
![]()
Dengan aturan Cramer, kita mengubah kolom kedua determinan A dengan kolom suku bebas dan membaginya dengan determinan A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 2 & \color{red}\bm{1} & 3 \\[1.1ex] 3 & \color{red}\bm{0} & -1 \\[1.1ex] 1 & \color{red}\bm{5} & 2\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{48}{24} = \bm{2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-08e3dabe2f33434eb96658491f67c0b4_l3.png)
Menghitung
![]()
Dengan aturan Cramer, kita mengubah kolom ketiga determinan A dengan kolom suku bebas dan membaginya dengan determinan A:
![Rendered by QuickLaTeX.com \displaystyle \bm{z} = \cfrac{\begin{vmatrix} 2 & 1 & \color{red}\bm{1} \\[1.1ex] 3 & -2 & \color{red}\bm{0} \\[1.1ex] 1 & 3 & \color{red}\bm{5}\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-24}{24} = \bm{-1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96e76cb8867224755e9c19254678abd4_l3.png)
Oleh karena itu, penyelesaian sistem persamaan tersebut adalah:
![]()
Contoh 2: Sistem Kompatibel Tak tentu (ICS)
- Selesaikan sistem persamaan berikut menggunakan aturan Cramer:
![Rendered by QuickLaTeX.com \begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \\[1.5ex] x+5y+3z = 1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-781530aac4d8507fd6c7cbd77c3b4651_l3.png)
Pertama-tama kita buat matriks A dan matriks perluasan A’ dari sistem:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 3 & 2 & 4 \\[1.1ex] -2 & 3 & -1 \\[1.1ex] 1 & 5 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & 2 & 4 & 1 \\[1.1ex] -2 & 3 & -1 & 0 \\[1.1ex] 1 & 5 & 3 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a64800a78bf8e2e2f547be907e6863cb_l3.png)
Sekarang kita menghitung rentang kedua matriks dan dengan demikian dapat melihat jenis sistemnya. Untuk menghitung rank A, kita menghitung determinan seluruh matriks (menggunakan aturan Sarrus) dan memeriksa apakah hasilnya 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & 2 & 4 \\[1.1ex] -2 & 3 & -1 \\[1.1ex] 1 & 5 & 3\end{vmatrix} = 27-2-40-12+15+12= 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-581c58cbe0fdd9952e7e25b919ecc33b_l3.png)
Penentunya menghasilkan 0, sehingga matriks A tidak berpangkat 3. Tetapi matriks A mempunyai determinan 2×2 yang berbeda dengan 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3 \end{vmatrix} =9-(-4)=13\neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-a5d1acad8bc31240f80d8cfbf3605997_l3.png)
Jadi matriks A mempunyai rangking 2 :
![]()
Setelah kita mengetahui luas matriks A, kita menghitung luas matriks A’. Penentu dari 3 kolom pertama menghasilkan 0, jadi kita coba kemungkinan determinan 3×3 lainnya pada matriks A’:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 4 & 1 \\[1.1ex] 3 & -1 & 0 \\[1.1ex] 5 & 3 & 1 \end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & 4 & 1 \\[1.1ex] -2 & -1 & 0 \\[1.1ex] 1 & 3 & 1 \end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & 2 & 1 \\[1.1ex] -2 & 3 & 0 \\[1.1ex] 1 & 5 & 1 \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-686e7ca635ecee685005f6013c2e64ad_l3.png)
Semua determinan berorde 3 menghasilkan 0. Namun, jelas bahwa matriks A’ mempunyai determinan non-0 2×2 yang sama dengan matriks A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3 \end{vmatrix} =9-(-4)=13\neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-a5d1acad8bc31240f80d8cfbf3605997_l3.png)
Oleh karena itu, matriks A’ juga mempunyai rangking 2 :
![]()
Jadi, karena pangkat matriks A sama dengan pangkat matriks A’ tetapi keduanya lebih kecil dari jumlah sistem yang tidak diketahui (3), kita mengetahui melalui teorema Rouché-Frobenius bahwa ini adalah Sistem yang Kompatibel Tak Pasti (ICS):
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96868a2569ea0ab5ca99d8dc606d3dc9_l3.png)
Ketika kita ingin menyelesaikan sistem tak tentu yang kompatibel (SCI), kita perlu mentransformasikan sistemnya : pertama-tama kita hilangkan persamaannya, kemudian kita ubah sebuah variabel menjadi λ (biasanya variabel z), dan terakhir kita satukan suku-suku yang memiliki λ dengan ketentuan independen.
Setelah kita mentransformasikan sistem, kita menerapkan aturan Cramer dan kita akan mendapatkan solusi sistem sebagai fungsi dari λ.
Dalam hal ini, kita akan menghilangkan persamaan terakhir dari sistem:
![Rendered by QuickLaTeX.com \begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \\[1.5ex]\cancel{x+5y+3z = 1} \end{cases} \longrightarrow \quad \begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f0511fecc9c2af695b6b8eccae6b0661_l3.png)
Sekarang mari kita ubah variabel z menjadi λ:
![Rendered by QuickLaTeX.com \begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 3x+2y+4\lambda=1 \\[1.5ex] -2x+3y-\lambda=0\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2d6142d2be611954fd849a032a97245a_l3.png)
Dan kami menempatkan suku dengan λ dengan suku independen:
![Rendered by QuickLaTeX.com \begin{cases} 3x+2y=1-4\lambda \\[1.5ex] -2x+3y=\lambda \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-00214205f2334f1c9bc10810c1c1df83_l3.png)
Oleh karena itu, matriks A dan matriks A’ dari sistem tersebut tetap:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 3 & 2 \\[1.1ex] -2 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 3 & 2 & 1 -4\lambda \\[1.1ex] -2 & 3 & \lambda \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-9c4b47303973b823a1c5628f5448ca79_l3.png)
Terakhir, setelah kita mengubah sistem, kita menerapkan aturan Cramer . Oleh karena itu, kita menyelesaikan determinan A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3\end{vmatrix} = 13](https://mathority.org/wp-content/ql-cache/quicklatex.com-d1b79f52dc82f5cfc311867273e78c06_l3.png)
Untuk menghitung hal yang tidak diketahui
![]()
Dengan aturan Cramer, kita ubah kolom pertama determinan A dengan kolom suku bebas dan membaginya dengan determinan A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 1 -4\lambda & 2 \\[1.1ex] \lambda & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3(1-4\lambda) -2\lambda}{13} = \cfrac{\bm{3-14\lambda} }{\bm{13}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0ff917eaea976c65bd18e0476078d3cb_l3.png)
Untuk menghitung hal yang tidak diketahui
![]()
Dengan aturan Cramer, kita mengubah kolom kedua determinan A dengan kolom suku bebas dan membaginya dengan determinan A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 3 & 1 -4\lambda \\[1.1ex]-2& \lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3\lambda -\bigl(-2(1-4\lambda)\bigr)}{13}= \cfrac{3\lambda -\bigl(-2+8\lambda\bigr)}{13} = \cfrac{\bm{2-5\lambda} }{\bm{13}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-155ca520739bbf7e040a6cdc632f7c27_l3.png)
Meskipun penyelesaian sistem persamaan tersebut adalah fungsi dari λ, karena merupakan SCI dan oleh karena itu, ia mempunyai banyak penyelesaian yang tak terhingga:
![]()
Aturan Cramer Memecahkan Masalah
Latihan 1
Terapkan aturan Cramer untuk menyelesaikan sistem dua persamaan berikut dengan 2 persamaan yang tidak diketahui:
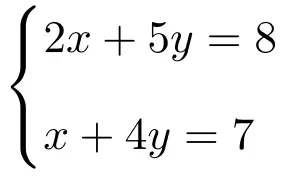
Hal pertama yang harus dilakukan adalah matriks A dan matriks perluasan A’ dari sistem:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{cc} 2 & 5 \\[1.1ex] 1 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 2 & 5 & 8 \\[1.1ex] 1 & 4 & 7 \end{array}\right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-2a001db9cf56846150730fee7126dacd_l3.png)
Sekarang kita harus mencari rank matriks A. Untuk melakukannya, kita periksa apakah determinan seluruh matriks berbeda dari 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 5 \\[1.1ex] 1 & 4 \end{vmatrix} = 8-5=3 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0c75c1c344c286016bea83237f1f418e_l3.png)
Karena matriks mempunyai determinan 2×2 yang berbeda dengan 0, maka matriks A mempunyai rank 2:
![]()
Setelah kita mengetahui pangkat A, kita menghitung pangkat A’. Ini paling tidak berada pada peringkat 2, karena kita baru saja melihat bahwa di dalamnya terdapat determinan berorde 2 yang berbeda dari 0. Selain itu, ia tidak dapat berada pada peringkat 3, karena kita tidak dapat tidak membuat determinan 3×3. Oleh karena itu, matriks A’ juga mempunyai rangking 2:
![]()
Oleh karena itu, dengan menerapkan teorema Rouché-Frobenius, kita mengetahui bahwa ini adalah sistem determinasi yang kompatibel (SCD), karena jangkauan A sama dengan jangkauan A’ dan jumlah yang tidak diketahui.
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 2 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 2 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bbd67b16bb6d52a0696e70a77833cd3b_l3.png)
Setelah kami mengetahui bahwa sistem tersebut adalah SCD, kami menerapkan aturan Cramer untuk menyelesaikannya.
Untuk menghitung hal yang tidak diketahui
![]()
Dengan aturan Cramer, kita ubah kolom pertama determinan A dengan kolom suku bebas dan membaginya dengan determinan A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 8 & 5 \\[1.1ex] 7 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-3}{3} = \bm{-1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b0adeda8f2ce557661466996038b1148_l3.png)
Untuk menghitung hal yang tidak diketahui
![]()
Dengan aturan Cramer, kita mengubah kolom kedua determinan A dengan kolom suku bebas dan membaginya dengan determinan A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix}2 & 8 \\[1.1ex] 1 & 7\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{6}{3} = \bm{2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-59790a66cc31fac07be1d5a7bb556d9e_l3.png)
Oleh karena itu, penyelesaian sistem persamaan tersebut adalah:
![]()
Latihan 2
Temukan solusi dari sistem tiga persamaan berikut dengan 3 yang tidak diketahui menggunakan aturan Cramer:
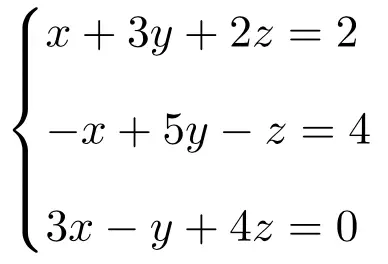
Pertama-tama kita buat matriks A dan matriks perluasan A’ dari sistem:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 1 & 3 & 2\\[1.1ex] -1 & 5 & -1\\[1.1ex] 3 & -1 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 3 & 2 & 2 \\[1.1ex] -1 & 5 & -1 & 4 \\[1.1ex] 3 & -1 & 4 & 0 \end{array}\right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-eea75fbf6d86ebc3d0b9e236cd2160f5_l3.png)
Sekarang kita mencari rank matriks A dengan menghitung determinan matriks 3×3 dengan aturan Sarrus:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 3 & 2 \\[1.1ex] -1 & 5 & -1\\[1.1ex] 3 & -1 & 4 \end{vmatrix} = 20-9+2-30-1+12=-6 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-73f751f3b5c527c16b5de1b10bf07a4e_l3.png)
Matriks yang mempunyai determinan orde 3 berbeda dengan 0, matriks A mempunyai rank 3:
![]()
akibatnya, matriks A’ juga menduduki peringkat 3:
![]()
Oleh karena itu, dengan menggunakan teorema Rouché-Frobenius, kita mengetahui bahwa ini adalah sistem determinasi yang kompatibel (SCD), karena jangkauan A sama dengan jangkauan A’ dan jumlah yang tidak diketahui.
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31b495a48a75d7af1f23e38818bf4eca_l3.png)
Setelah kita mengetahui bahwa sistem tersebut adalah SCD, kita perlu menerapkan aturan Cramer untuk menyelesaikan sistem tersebut.
Untuk menghitung hal yang tidak diketahui
![]()
Dengan aturan Cramer, kita ubah kolom pertama determinan A dengan kolom suku bebas dan membaginya dengan determinan A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2 & 3 & 2 \\[1.1ex] 4 & 5 & -1\\[1.1ex]0 & -1 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-18}{-6} = \bm{3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fc574297f609b68e4fb48466ec6c8077_l3.png)
Untuk menghitung hal yang tidak diketahui
![]()
Dengan aturan Cramer, kita mengubah kolom kedua determinan A dengan kolom suku bebas dan membaginya dengan determinan A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix}1 & 2 & 2 \\[1.1ex] -1 & 4 & -1\\[1.1ex] 3 & 0 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-6}{-6} = \bm{1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2544601137d62e217ff1866f278203d6_l3.png)
Menghitung
![]()
Dengan aturan Cramer, kita mengubah kolom ketiga determinan A dengan kolom suku bebas dan membaginya dengan determinan A:
![Rendered by QuickLaTeX.com \displaystyle \bm{z} = \cfrac{\begin{vmatrix} 1 & 3 & 2 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 3 & -1 & 0\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{12}{-6} = \bm{-2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-42d7d4adcfc48954185ca14b56b8e128_l3.png)
Oleh karena itu, penyelesaian sistem persamaan tersebut adalah:
![]()
Latihan 3
Hitung solusi sistem tiga persamaan berikut dengan 3 yang tidak diketahui menggunakan aturan Cramer:
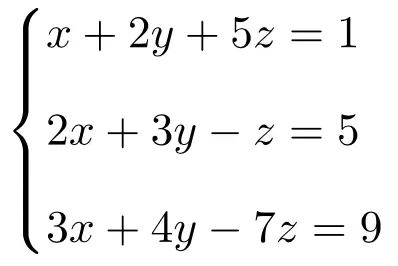
Pertama-tama kita buat matriks A dan matriks perluasan A’ dari sistem:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 1 & 2 & 5\\[1.1ex] 2 & 3 & -1 \\[1.1ex] 3 & 4 & -7 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 2 & 5 & 1 \\[1.1ex] 2 & 3 & -1 & 5 \\[1.1ex] 3 & 4 & -7 & 9 \end{array}\right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-afd359275e5ebaaf3229504c47a5815f_l3.png)
Kami menghitung luas matriks A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 2 & 5\\[1.1ex] 2 & 3 & -1 \\[1.1ex] 3 & 4 & -7 \end{vmatrix} =-21-6+40-45+4+28=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-47ddf17a2b3eed5a680d685900a79b31_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3 \end{vmatrix} = 3-4 = -1 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-fdd4380c7c76418bd3ec12c94359f886_l3.png)
![]()
Setelah kita mengetahui luas matriks A, kita menghitung luas matriks A’. Penentu dari 3 kolom pertama menghasilkan 0, jadi kita coba kemungkinan determinan 3×3 lainnya pada matriks A’:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 5 & 1 \\[1.1ex] 3 & -1 & 5 \\[1.1ex] 4 & -7 & 9 \end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 5 & 1 \\[1.1ex] 2 & -1 & 5 \\[1.1ex] 3 & -7 & 9\end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 2 & 1 \\[1.1ex] 2 & 3 & 5 \\[1.1ex] 3 & 4 & 9 \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-1addc62130e0462075b3bade26a7e35e_l3.png)
Semua determinan berorde 3 menghasilkan 0. Namun matriks A’ mempunyai determinan non-0 2×2 yang sama dengan matriks A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3 \end{vmatrix} = 3-4 = -1 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-7de377466bd5afd03f58f9b532324e75_l3.png)
Oleh karena itu, matriks A’ juga mempunyai rangking 2:
![]()
Karena pangkat matriks A sama dengan pangkat matriks A’ tetapi keduanya lebih kecil dari jumlah sistem yang tidak diketahui (3), kita mengetahui melalui teorema Rouché-Frobenius bahwa ini adalah Sistem Kompatibel Tak tentu (ICS):
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96868a2569ea0ab5ca99d8dc606d3dc9_l3.png)
Sebagai sistem ICS, kita harus menghilangkan persamaan. Dalam hal ini, kita akan menghilangkan persamaan terakhir dari sistem:
![Rendered by QuickLaTeX.com \begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5 \\[1.5ex]\cancel{3x+4y-7z = 9} \end{cases} \longrightarrow \quad \begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3a1d067e155540f4345cf56e5c1567d3_l3.png)
Sekarang mari kita ubah variabel z menjadi λ:
![Rendered by QuickLaTeX.com \begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} x+2y+5\lambda=1 \\[1.5ex] 2x+3y-\lambda=5\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b5fa91777a722d3783b2f887aab44152_l3.png)
Dan kami menempatkan suku dengan λ dengan suku independen:
![Rendered by QuickLaTeX.com \begin{cases} x+2y=1-5\lambda\\[1.5ex] 2x+3y=5+\lambda \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-76ff21181be050b01c247981298986a7_l3.png)
Sehingga matriks A dan matriks A’ sistem tetap:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 1 & 2 \\[1.1ex] 2 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 1 & 2 & 1 -5\lambda \\[1.1ex] 2 & 3 &5+\lambda \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-230e5b28dd467127e63f4f9756cf90da_l3.png)
Terakhir, setelah kita mengubah sistem, kita menerapkan aturan Cramer . Oleh karena itu, kita menyelesaikan determinan A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3\end{vmatrix} =-1](https://mathority.org/wp-content/ql-cache/quicklatex.com-f127efbd217e2bca8852ec792610732f_l3.png)
Untuk menghitung hal yang tidak diketahui
![]()
Dengan aturan Cramer, kita ubah kolom pertama determinan A dengan kolom suku bebas dan membaginya dengan determinan A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 1-5\lambda & 2 \\[1.1ex] 5+\lambda & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3-15\lambda -(10+2\lambda)}{-1} = \cfrac{-7-17\lambda}{-1} = \bm{7+17\lambda}](https://mathority.org/wp-content/ql-cache/quicklatex.com-42652a14362b42e606841b6bb3e77cc0_l3.png)
Untuk menghitung hal yang tidak diketahui
![]()
Dengan aturan Cramer, kita mengubah kolom kedua determinan A dengan kolom suku bebas dan membaginya dengan determinan A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 1 & 1-5\lambda \\[1.1ex] 2 & 5+\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{5+\lambda -(2-10\lambda)}{-1}= \cfrac{3+11\lambda}{-1} = \bm{-3-11\lambda}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b95c5870f1762a2d82c9ebcccbca7408_l3.png)
Meskipun penyelesaian sistem persamaan tersebut adalah fungsi dari λ, karena merupakan SCI dan oleh karena itu, ia mempunyai banyak penyelesaian yang tak terhingga:
![]()
Latihan 4
Selesaikan soal sistem tiga persamaan dengan 3 variabel tak diketahui berikut ini dengan menerapkan aturan Cramer:
![Rendered by QuickLaTeX.com \begin{cases} -2x+5y+z=8 \\[1.5ex] 6x+2y+4z=4 \\[1.5ex] 3x-2y+z = -2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-61e1c3458f33b863db10750b9e51d09e_l3.png)
Pertama, kita membuat matriks A dan matriks perluasan A’ dari sistem:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc}-2 & 5 & 1 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & 1\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} -2 & 5 & 1 & 8 \\[1.1ex] 6 & 2 & 4 & 4 \\[1.1ex] 3 & -2 & 1 & -2 \end{array}\right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-743a40010cb4a610e8a3fc6ae5d313b4_l3.png)
Sekarang mari kita hitung rank matriks A dengan menghitung determinan matriks 3×3 menggunakan aturan Sarrus:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} -2 & 5 & 1 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & 1 \end{vmatrix} = -4+60-12-6-16-30=-8 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-713c634fbc3e1b1cb228e3891c9bff1c_l3.png)
Matriks yang mempunyai determinan orde 3 berbeda dengan 0, matriks A mempunyai rank 3:
![]()
akibatnya matriks A’ juga mempunyai rangking 3, karena paling sedikit harus mempunyai rangking yang sama dengan matriks A dan tidak boleh mempunyai rangking 4 karena matriks tersebut berdimensi 3×4.
![]()
Oleh karena itu, dengan menggunakan teorema Rouché-Frobenius, kami menyimpulkan bahwa ini adalah sistem yang kompatibel dengan determinasi (SCD), karena jangkauan A sama dengan jangkauan A’ dan jumlah yang tidak diketahui.
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31b495a48a75d7af1f23e38818bf4eca_l3.png)
Setelah kita mengetahui bahwa sistem tersebut adalah SCD, kita perlu menerapkan aturan Cramer untuk menyelesaikan sistem tersebut.
Untuk menghitung hal yang tidak diketahui
![]()
Dengan aturan Cramer, kita ubah kolom pertama determinan A dengan kolom suku bebas dan membaginya dengan determinan A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 8 & 5 & 1 \\[1.1ex] 4 & 2 & 4 \\[1.1ex] -2 & -2 & 1\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{16}{-8} = \bm{-2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8a290479c69ff806f19dcf29f96e1228_l3.png)
Untuk menghitung hal yang tidak diketahui
![]()
Dengan aturan Cramer, kita mengubah kolom kedua determinan A dengan kolom suku bebas dan membaginya dengan determinan A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix}-2 & 8 & 1 \\[1.1ex] 6 & 4 & 4 \\[1.1ex] 3 & -2 & 1\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-6} = \bm{0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8bba0765fbcbcebf0585520af25b4a30_l3.png)
Menghitung
![]()
Dengan aturan Cramer, kita mengubah kolom ketiga determinan A dengan kolom suku bebas dan membaginya dengan determinan A:
![Rendered by QuickLaTeX.com \displaystyle \bm{z} = \cfrac{\begin{vmatrix} -2 & 5 & 8 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & -2\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-32}{-8} = \bm{4}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5bc157a8c4dfe8ee4651affac68ef878_l3.png)
Oleh karena itu, penyelesaian sistem persamaan linear adalah:
![]()
Latihan 5
Selesaikan sistem persamaan linear berikut menggunakan aturan Cramer:
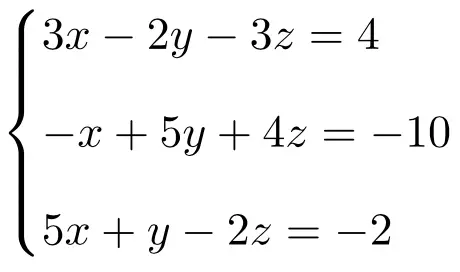
Pertama-tama kita buat matriks A dan matriks perluasan A’ dari sistem:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 3 & -2 & -3 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 5 & 1 & -2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & -2 & -3 & 4 \\[1.1ex] -1 & 5 & 4 & -10 \\[1.1ex] 5 & 1 & -2 & -2 \end{array}\right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f5153b5951b768cc3cafa2bb2567ba92_l3.png)
Kami menghitung luas matriks A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & -2 & -3 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 5 & 1 & -2 \end{vmatrix} =-30-40+3+75-12+4=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-f3778c9499e2a44ea3834dfed1523163_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & -2 \\[1.1ex] -1 & 5 \end{vmatrix} = 15- (2)= 13 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-03d70742b14ced92f33963df0c86e92f_l3.png)
![]()
Setelah kita mengetahui luas matriks A, kita menghitung luas matriks A’. Penentu dari 3 kolom pertama menghasilkan 0, jadi kita coba kemungkinan determinan 3×3 lainnya pada matriks A’:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -2 & -3 & 4 \\[1.1ex] 5 & 4 & -10 \\[1.1ex] 1 & -2 & -2 \end{vmatrix} = 0 \qquad \begin{vmatrix}3 & -3 & 4 \\[1.1ex] -1 & 4 & -10 \\[1.1ex] 5 & -2 & -2\end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & -2 & 4 \\[1.1ex] -1 & 5 & -10 \\[1.1ex] 5 & 1 &-2\end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-5bed93d532ae4ccd4649a73662f55f0f_l3.png)
Semua determinan berorde 3 menghasilkan 0. Namun, jelas matriks A’ mempunyai determinan berorde 2 selain 0 yang sama dengan matriks A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & -2 \\[1.1ex] -1 & 5 \end{vmatrix} = 13 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-858d95d7d252b16706b66c0e6aba09c4_l3.png)
Oleh karena itu, matriks A’ juga mempunyai rangking 2:
![]()
Pangkat matriks A sama dengan pangkat matriks A’ tetapi keduanya lebih kecil dari jumlah yang tidak diketahui dari sistem (3), sehingga berdasarkan teorema Rouché-Frobenius kita mengetahui bahwa matriks tersebut merupakan Indeterminate System Kompatibel (SCI) :
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96868a2569ea0ab5ca99d8dc606d3dc9_l3.png)
Sebagai sistem ICS, kita harus menghilangkan satu persamaan. Dalam hal ini, kita akan menghilangkan persamaan terakhir dari sistem:
![Rendered by QuickLaTeX.com \begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10 \\[1.5ex]\cancel{5x+y-2z = -2} \end{cases} \longrightarrow \quad \begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4e10bd826663dff41c4272610cbc07b1_l3.png)
Sekarang mari kita ubah variabel z menjadi λ:
![Rendered by QuickLaTeX.com \begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 3x-2y-3\lambda=4 \\[1.5ex] -x+5y+4\lambda=-10\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2502be450040b38761c08e5d6beaf379_l3.png)
Dan kami menempatkan suku dengan λ dengan suku independen:
![Rendered by QuickLaTeX.com \begin{cases} 3x-2y=4+3\lambda \\[1.5ex] -x+5y=-10-4\lambda\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-80a43d98e6be30965d554e8a89aa5d89_l3.png)
Sehingga matriks A dan matriks A’ sistem tetap:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 3 & -2 \\[1.1ex] -1 & 5 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 3 & -2 & 4+3\lambda \\[1.1ex] 1 & 5 &-10-4\lambda \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3451ce571163983cf41794d4998283d6_l3.png)
Terakhir, setelah kita mengubah sistem, kita menerapkan aturan Cramer . Oleh karena itu, kita menyelesaikan determinan A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}3& -2 \\[1.1ex] -1 & 5\end{vmatrix} =13](https://mathority.org/wp-content/ql-cache/quicklatex.com-0e7a7d6208ea5e762f5c74a44e6838cf_l3.png)
Untuk menghitung hal yang tidak diketahui
![]()
Dengan aturan Cramer, kita ubah kolom pertama determinan A dengan kolom suku bebas dan membaginya dengan determinan A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 4+3\lambda & -2 \\[1.1ex]-10-4\lambda & 5\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{20+15\lambda -(20+8\lambda)}{13} = \cfrac{\bm{7\lambda}}{\bm{13}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8c30fcc0526c2d4112eb4f60a3d8847f_l3.png)
Untuk menghitung hal yang tidak diketahui
![]()
Dengan aturan Cramer, kita mengubah kolom kedua determinan A dengan kolom suku bebas dan membaginya dengan determinan A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 3 & 4+3\lambda \\[1.1ex] -1 & -10-4\lambda\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-30-12\lambda -(-4-3\lambda)}{13}= \cfrac{\bm{-26-9\lambda}}{\bm{13}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fdb22a54274e019c811c9051502c474a_l3.png)
Jadi, solusi sistem persamaan adalah fungsi dari λ, karena merupakan SCI dan, oleh karena itu, sistem tersebut memiliki banyak solusi yang tak terhingga:
![]()