Pada halaman ini Anda akan mempelajari apa itu determinan matriks persegi 3×3. Anda akan melihat cara menyelesaikan determinan orde 3 menggunakan aturan Sarrus. Selain itu, Anda memiliki contoh dan latihan yang diselesaikan selangkah demi selangkah, sehingga Anda dapat mempraktikkannya dan memahaminya dengan sempurna.
Berapakah determinan matriks 3×3?
Penentu orde 3 adalah matriks berdimensi 3×3 yang diwakili oleh garis vertikal pada setiap sisi matriks. Misalnya, jika kita mempunyai matriks berikut:
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} 2 & 0 & 4 \\[1.1ex] 3 & -1 & 5 \\[1.1ex] 1 & 6 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7b5e89b706893e88dd15882e3685afb1_l3.png)
Penentu matriks A direpresentasikan sebagai berikut:
![Rendered by QuickLaTeX.com \displaystyle \lvert A \rvert = \begin{vmatrix} 2 & 0 & 4 \\[1.1ex] 3 & -1 & 5 \\[1.1ex] 1 & 6 & -2 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-41db04327de87a80f1e0e4dd6dcb220a_l3.png)
Seperti yang Anda lihat, menulis determinan matriks persegi berorde 3 itu mudah. Sekarang mari kita lihat cara mengatasinya:
Bagaimana cara menghitung determinan orde 3?
Untuk membuat determinan matriks 3×3 harus menerapkan aturan Sarrus :
pemerintahan Sarrus
Aturan Sarrus mengatakan bahwa untuk menghitung determinan orde 3, kita harus menjumlahkan hasil kali elemen-elemen diagonal mayor dan hasil kali diagonal-diagonal sejajarnya dengan titik-titik yang berlawanan, lalu mengurangkan hasil kali elemen-elemen diagonal minor dan hasil kali diagonal-diagonal sejajarnya dengan titik-titik sudut yang berhadapan.
Ditulis seperti itu mungkin agak sulit untuk dipahami, namun lihatlah cara perhitungan determinan 3×3 dengan diagram dan contoh berikut:


Contoh determinan 3×3:
![Rendered by QuickLaTeX.com \begin{aligned} \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] -1 & 1 & 0 \\[1.1ex] -2 & 4 & 1 \end{vmatrix} & = 2 \cdot 1 \cdot 1 + 1 \cdot 0 \cdot (-2) + (-1) \cdot 4 \cdot 3 - (-2) \cdot 1 \cdot 3 - 4 \cdot 0 \cdot 2- (-1) \cdot 1 \cdot 1 \\ & = 2 + 0 -12 +6 - 0 +1 \\[2ex] & = \bm{-3} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-98e60cf465cd0eb7662d47770cd38231_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} \begin{vmatrix} 1 & 0 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 4 & -3 & -1 \end{vmatrix} & = 1\cdot 2 \cdot (-1) + 0 \cdot 1 \cdot 4 +3 \cdot (-3) \cdot 2 - 4 \cdot 2 \cdot 2 - (-3) \cdot 1 \cdot 1- 3 \cdot 0 \cdot (-1) \\ & = -2 +0 -18 - 16 +3- 0 \\[2ex] & = \bm{-33} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-41a53c1fd6eae1b51a280a6ce1e2ab91_l3.png)
Menyelesaikan masalah determinan matriks 3×3
Latihan 1
Selesaikan determinan 3×3 berikut:
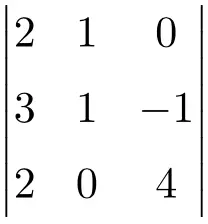
Untuk menyelesaikan determinan matriks 3×3 kita harus menerapkan aturan Sarrus:
![Rendered by QuickLaTeX.com \displaystyle\begin{aligned} \begin{vmatrix} 2 & 1 & 0 \\[1.1ex] 3 & 1 & -1 \\[1.1ex] 2 & 0 & 4 \end{vmatrix} & = 2 \cdot 1 \cdot 4 + 1 \cdot (-1) \cdot 2 + 3 \cdot 0 \cdot 0 - 2 \cdot 1 \cdot 0 - 0 \cdot (-1) \cdot 2- 3 \cdot 1 \cdot 4 \\ & = 8 -2 +0 -0- 0-12 \\[2ex] & = \bm{-6} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8f288312b72f3bbabc35ee64bf580d8c_l3.png)
Latihan 2
Hitung determinan orde 3 berikut:
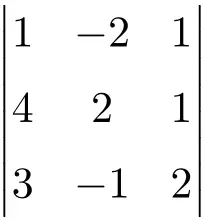
Untuk menghitung determinan matriks orde ketiga, kita harus menggunakan aturan Sarrus:
![Rendered by QuickLaTeX.com \displaystyle\begin{aligned} \begin{vmatrix} 1 & -2 & 1 \\[1.1ex] 4 & 2 & 1 \\[1.1ex] 3 & -1 & 2 \end{vmatrix} & = 1 \cdot 2 \cdot 2 + (-2) \cdot 1 \cdot 3 + 4 \cdot (-1) \cdot 1 - 3 \cdot 2 \cdot 1 - (-1) \cdot 1 \cdot 1 - 4 \cdot (-2) \cdot 2 \\ & = 4 -6 -4 -6+1+16 \\[2ex] & = \bm{5} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-64078968233ec50d2e793309d55e55fc_l3.png)
Latihan 3
Tentukan penyelesaian determinan matriks 3×3 berikut:
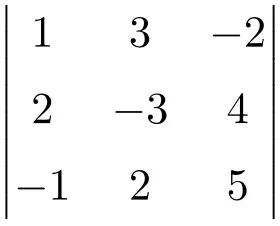
Untuk menentukan determinan matriks 3×3, kita harus menggunakan aturan Sarrus:
![Rendered by QuickLaTeX.com \displaystyle\begin{aligned} \begin{vmatrix}1 & 3 & -2 \\[1.1ex] 2 & -3 & 4 \\[1.1ex] -1 & 2 & 5 \end{vmatrix} & = \\ & = 1 \cdot (-3) \cdot 5 + 3 \cdot 4 \cdot (-1) + 2 \cdot 2 \cdot (-2) \ - \\[1.1ex] & \phantom{=} - (-1) \cdot (-3) \cdot (-2) - 2 \cdot 4 \cdot 1 - 2 \cdot 3 \cdot 5 \\[2.5ex] & = -15 -12 -8 +6-8-30 \\[2.5ex] & = \bm{-67} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fd4494ae66a604834b8f9f47fcbbe41d_l3.png)
Latihan 4
Tentukan penyelesaian determinan matriks orde 3 berikut:
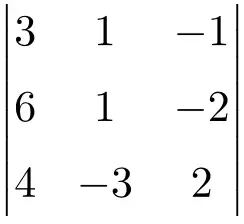
Untuk mencari solusi determinan matriks 3×3 kita harus menerapkan rumus Sarrus:
![Rendered by QuickLaTeX.com \displaystyle\begin{aligned} \begin{vmatrix} 3 & 1 & -1 \\[1.1ex] 6 & 1 & -2 \\[1.1ex] 4 & -3 & 2 \end{vmatrix} & = \\ & = 3 \cdot 1 \cdot 2 + 1 \cdot (-2) \cdot 4 + 6 \cdot (-3) \cdot (-1) \ - \\[1.1ex] & \phantom{=} - 4 \cdot 1 \cdot (-1) - (-3) \cdot (-2) \cdot 3 - 6 \cdot 1 \cdot 2 \\[2.5ex] & =6 -8 +18 +4-18-12 \\[2.5ex] & = \bm{-10} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8e811024d460a60a1df59983b1f700e8_l3.png)
Latihan 5
temukan nilai dari
![]()
yang membatalkan determinan orde ketiga berikut:
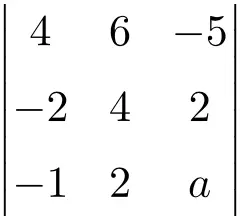
Pertama-tama kita menghitung, dengan aturan Sarrus, nilai determinan sebagai fungsi dari
![]()
![Rendered by QuickLaTeX.com \displaystyle\begin{aligned}\begin{vmatrix} 4 & 6 & -5 \\[1.1ex] -2 & 4 & 2 \\[1.1ex] -1 & 2 & a \end{vmatrix} & = \\ & = 4 \cdot 4 \cdot a + 6 \cdot 2 \cdot (-1) + (-2) \cdot 2 \cdot (-5) \ - \\[1.1ex] & \phantom{=}- (-1) \cdot 4 \cdot (-5) - 2 \cdot 2 \cdot 4 - (-2) \cdot 6 \cdot a \\[2.5ex] & = 16a -12 + 20 - 20 - 16 +12a \\[2.5ex] & = 28a -28 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-07e67cfc5e45c0a11c35d643cd4c1c78_l3.png)
Agar determinannya hilang, hasilnya harus 0. Oleh karena itu, kita tetapkan hasilnya sama dengan 0 dan selesaikan persamaannya:
![]()
![]()
![]()