Di halaman ini kami menjelaskan cara mengurangkan polinomial. Selain itu, Anda akan menemukan beberapa contoh dan menyelesaikan latihan langkah demi langkah untuk mengurangkan polinomial.
Bagaimana cara mengurangi polinomial?
Untuk mengurangkan dua polinomial, Anda harus mengurangkan suku-suku polinomial yang sebangun. Dengan kata lain, pengurangan polinomial terdiri dari pengurangan suku-suku yang mempunyai bagian literal yang sama (variabel dan eksponen yang sama).
Dalam matematika, Anda dapat menghitung pengurangan polinomial dengan dua cara berbeda: dengan metode vertikal atau dengan metode horizontal. Di bawah ini adalah penjelasan dari kedua prosedur tersebut, namun kami menyarankan Anda untuk mempelajari cara mengurangkan polinomial secara vertikal terlebih dahulu, kemudian beralih ke metode horizontal. Tentu saja tetap dengan yang Anda sukai.
Pengurangan polinomial vertikal
Selanjutnya, kita akan melihat bagaimana dua polinomial dikurangkan secara vertikal menggunakan contoh:
- melakukan pengurangan
menjadi dua polinomial:
![]()
![]()
Hal pertama yang perlu kita lakukan untuk mencari pengurangan polinomial adalah menempatkan satu polinomial di bawah polinomial lainnya, sehingga suku-suku sejenis dari kedua polinomial tersebut sejajar dalam kolom:
Peringatan: Jika suatu polinomial tidak mempunyai suku dengan derajat tertentu, ruangnya harus dikosongkan. Misalnya polinomial
![]()
tidak mempunyai monomial kuadrat, sehingga terdapat ruang kosong pada tempatnya.
Meskipun sekarang kita dapat mengurangkan polinomial secara langsung, cukup mudah untuk mendapatkan tanda yang salah jika kita melakukannya dengan cara ini. Oleh karena itu, untuk melakukan pengurangan polinomial, yang terbaik adalah mengubah tanda semua suku pada polinomial pengurangan (polinomial pengurangan) dan kemudian melakukan penjumlahan. Karena mengurangkan suatu polinomial sama dengan menjumlahkan polinomial lawannya.
Dan setelah kita mengurutkan semua suku dari derajat tertinggi ke derajat terendah dan meniadakan suku-suku polinomial di bawah ini, kita tambahkan koefisien setiap kolom agar bagian literalnya tetap sama:
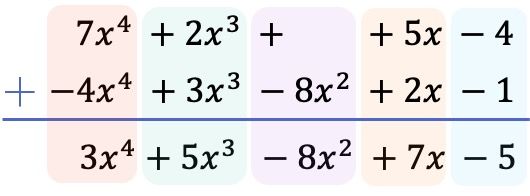
Oleh karena itu, hasil yang diperoleh dari pengurangan 2 polinomial tersebut adalah:
![]()
Jika langkah terakhir belum jelas bagi Anda, saya tinggalkan penjelasan tentang cara melakukan penjumlahan polinomial , sebenarnya Anda harus menguasai penjumlahan polinomial agar berhasil mengurangkan polinomial. Pada halaman tertaut Anda juga akan menemukan contoh dan penyelesaian latihan penjumlahan polinomial dan, sebagai tambahan, Anda akan dapat melihat perbedaan antara penjumlahan dan pengurangan polinomial.
Pengurangan polinomial horizontal
Kita baru saja melihat cara mengurangkan polinomial secara vertikal, namun sekarang kita akan melihat metode lain yang ada untuk mengurangkan polinomial: mengurangkan polinomial secara horizontal. Prosedur ini tentunya lebih cepat dari prosedur sebelumnya, namun Anda harus memiliki penguasaan konsep polinomial yang unggul.
Jadi mari kita lihat apa saja metode pengurangan polinomial ini melalui sebuah contoh. Agar Anda dapat melihat perbedaan antara kedua metode tersebut, kita akan mengurangkan polinomial yang sama seperti pada contoh sebelumnya:
- Hitung sisanya
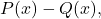
menjadi dua polinomial:
![]()
![]()
Pertama-tama kita harus meletakkan kedua polinomial tersebut dalam bentuk operasi aljabar, yaitu satu demi satu:
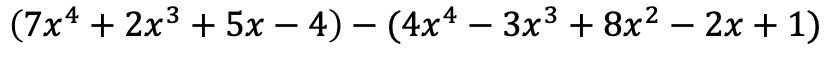
Monomial dalam tanda kurung pertama tetap sama, namun suku dalam tanda kurung kedua harus berubah tanda karena memiliki negatif di depannya:
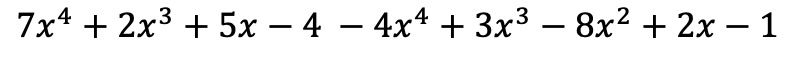
Dan sekarang kita mengelompokkan suku-suku yang memiliki bagian literal yang identik, yaitu suku-suku dengan variabel (huruf) dan eksponen yang sama. Suku-suku yang tidak sama tidak dapat ditambah atau dikurangi.
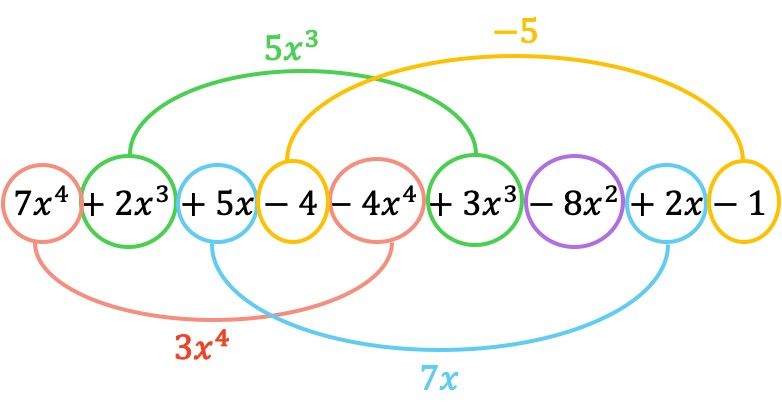
Jadi polinomial hasil pengurangannya adalah:
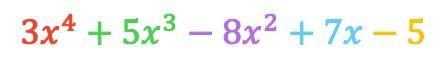
Seperti yang Anda lihat, kami mendapatkan hasil yang sama dengan kedua metode tersebut, jadi Anda dapat menggunakan mana yang paling cocok untuk Anda.
Sekarang setelah kamu melihat 2 cara menyelesaikan pengurangan polinomial, tahukah kamu bahwa kamu juga bisa mengurangkan pecahan dengan polinomial? Dan bukan hanya pengurangan, tetapi semua jenis operasi. Cari tahu bagaimana operasi pecahan aljabar dilakukan dengan mengklik tautan ini.
Menyelesaikan masalah pengurangan polinomial
Agar Anda dapat berlatih, kami memberikan beberapa latihan pengurangan polinomial yang telah diselesaikan. Jika Anda memiliki pertanyaan tentang latihan, Anda dapat menanyakannya di komentar di halaman, kami akan menjawabnya sesegera mungkin.
Latihan 1
Kurangi polinomialnya
![]()
dikurangi polinomialnya
![]()
![]()
![]()
Dalam hal ini, kita akan mengurangkan kedua polinomial secara vertikal. Untuk melakukan ini, pertama-tama kita mengurutkan polinomial berdasarkan derajat, kemudian kita mengubah tanda suku polinomial yang tersisa dan, terakhir, kita menjumlahkan monomial yang terletak di kolom yang sama:
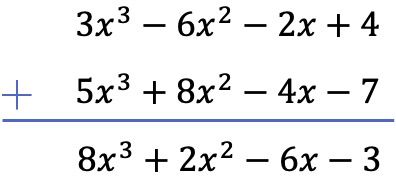
Latihan 2
Selesaikan polinomial pengurangan
![]()
dikurangi polinomialnya
![]()
![]()
![]()
Mengurangi dua polinomial sama dengan menambahkan kebalikan dari polinomial yang dikurangkan ke polinomial kecil. Oleh karena itu, kita ubah tanda suku polinomial subkontrak (yang tersisa) dan tambahkan polinomialnya:
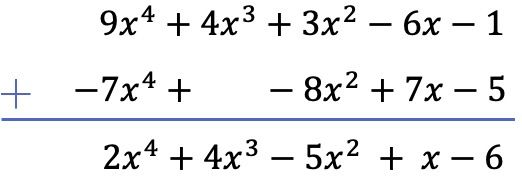
Perhatikan bahwa dalam kasus khusus ini harus ada ruang kosong di kolom derajat 3 dari polinomial kedua, karena tidak mempunyai suku derajat ketiga.
Latihan 3
Temukan hasil pengurangan polinomial
![]()
dikurangi polinomialnya
![]()
![]()
![]()
Dalam hal ini, kita akan menyelesaikan pengurangan dua polinomial secara vertikal. Jadi, pertama-tama kita urutkan polinomialnya dari derajat terbesar ke terkecil, lalu kita ubah tanda suku-suku polinomial yang tersisa dan terakhir, kita tambahkan suku-suku serupa:
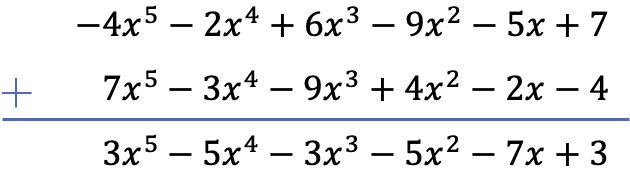
Latihan 4
Hitung operasi berikut dengan polinomial:
![]()
![]()
![]()
![]()
Dalam hal ini, 3 polinomial terlibat dalam operasi, 2 di antaranya merupakan pengurangan. Oleh karena itu, untuk menyelesaikan operasi ini, kita akan mengubah tanda semua suku dari dua polinomial yang tersisa dan kemudian kita akan menjumlahkan polinomial tersebut.
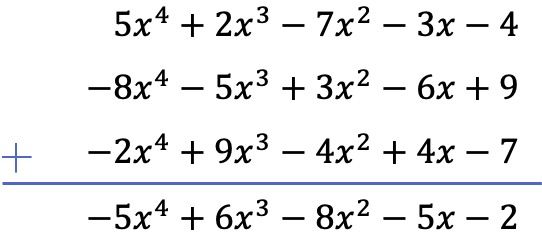
Bagaimana menurut Anda penjelasannya? Apakah menurut Anda hal itu bermanfaat? Metode pengurangan polinomial mana yang Anda sukai, vertikal atau horizontal? Kami membaca Anda di komentar! 👀