Kekuatan matriks -

Pada halaman ini kita akan melihat bagaimana melakukan perpangkatan matriks. Anda juga akan menemukan contoh dan latihan pangkat matriks yang diselesaikan selangkah demi selangkah yang akan membantu Anda memahaminya dengan sempurna. Anda juga akan mempelajari apa itu pangkat ke-n suatu matriks dan cara mencarinya.

Bagaimana cara menghitung kekuatan matriks?

Untuk menghitung pangkat suatu matriks , Anda harus mengalikan matriks dengan matriks itu sendiri sebanyak yang dinyatakan eksponennya. Misalnya:

$A^4 = A \cdot A \cdot A \cdot A$

Oleh karena itu, untuk mendapatkan pangkat suatu matriks, Anda perlu mengetahui cara menyelesaikan perkalian matriks . Jika tidak, Anda tidak dapat menghitung matriks pangkat.

Contoh penghitungan pangkat suatu matriks:

Oleh karena itu, pangkat matriks kuadrat dihitung dengan mengalikan matriks tersebut dengan matriks itu sendiri. Demikian pula, matriks pangkat tiga sama dengan matriks kuadrat dari matriks itu sendiri. Demikian pula, untuk mencari pangkat suatu matriks yang dipangkatkan menjadi empat, matriks yang dipangkatkan menjadi tiga harus dikalikan dengan matriks itu sendiri. Dan seterusnya.

Ada sifat penting dari pangkat matriks yang harus Anda ketahui: pangkat suatu matriks hanya dapat dihitung jika matriks tersebut berbentuk persegi , yaitu jika jumlah baris dan kolomnya sama.

Berapakah pangkat n suatu matriks?

Pangkat ke-n suatu matriks adalah ekspresi yang memudahkan kita menghitung pangkat apa pun dari suatu matriks.

Seringkali pangkat matriks mengikuti suatu pola . Oleh karena itu, jika kita dapat menguraikan barisan yang diikutinya, kita akan dapat menghitung pangkat apa pun tanpa harus melakukan semua perkalian.

Artinya, kita dapat menemukan rumus yang memberikan pangkat ke-n dari sebuah matriks tanpa harus menghitung semua pangkatnya.

Kiat untuk menemukan pola yang diikuti oleh pangkat:

Paritas eksponen . Mungkin saja pangkat genap ada di satu arah dan pangkat ganjil ada di arah lain.
Variasi tanda. Misalnya, bisa saja unsur pangkat genap bernilai positif dan unsur pangkat ganjil bernilai negatif, atau sebaliknya.
Pengulangan: apakah matriks yang sama diulang setiap sejumlah pangkat tertentu atau tidak.
Kita juga harus melihat apakah ada hubungan antara eksponen dan elemen matriks.

Contoh penghitungan pangkat n suatu matriks:

Menjadi
$A$

matriks berikut, hitunglah

$A^n$

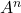
Dan

$A^{100}$

.

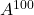
$\displaystyle A = \begin{pmatrix} 1 & 1 \\[1.1ex] 1 & 1 \end{pmatrix}$

Pertama-tama kita akan menghitung beberapa pangkat matriks

$A$

, untuk mencoba menebak pola yang diikuti oleh pangkat. Jadi kami menghitung

$A^2$

$A^3$

$A^4$

Dan

$A^5:$

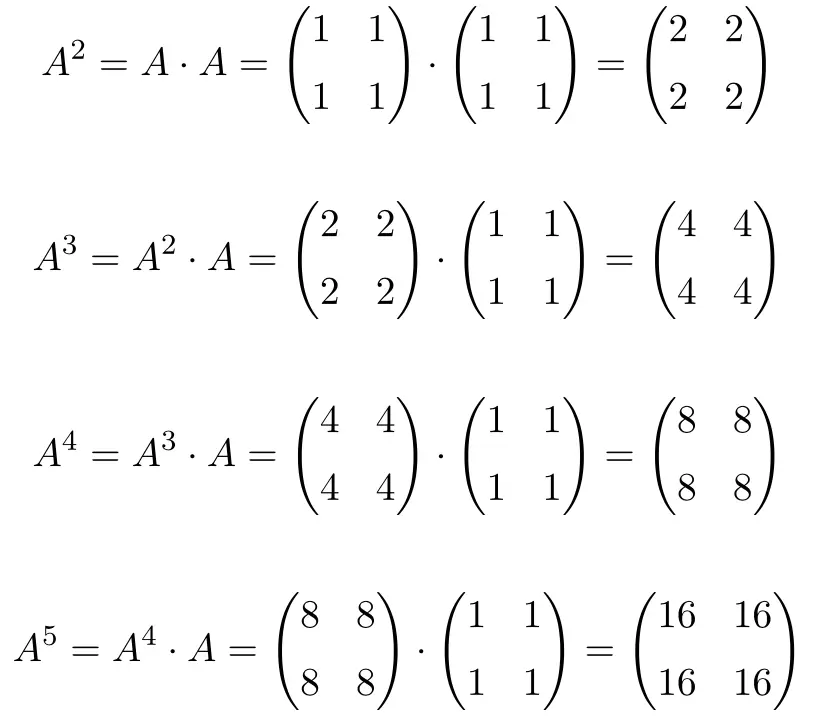
latihan diselesaikan selangkah demi selangkah dari pangkat matriks 2x2

Saat menghitung hingga

$A^5$

, kita melihat bahwa kekuatan matriks

$A$

Mereka mengikuti sebuah pola: untuk setiap peningkatan pangkat, hasilnya dikalikan dengan 2. Oleh karena itu, semua matriks adalah pangkat 2:

$\displaystyle A^2= \begin{pmatrix} 2 & 2 \\[1.1ex] 2 & 2 \end{pmatrix} =\begin{pmatrix} 2^1 & 2^1 \\[1.1ex] 2^1 & 2^1 \end{pmatrix}$

$\displaystyle A^3= \begin{pmatrix} 4 & 4 \\[1.1ex] 4 & 4 \end{pmatrix}=\begin{pmatrix} 2^2 & 2^2 \\[1.1ex] 2^2 & 2^2 \end{pmatrix}$

$\displaystyle A^4= \begin{pmatrix} 8 & 8 \\[1.1ex] 8 & 8 \end{pmatrix}=\begin{pmatrix} 2^3 & 2^3 \\[1.1ex] 2^3 & 2^3 \end{pmatrix}$

$\displaystyle A^5= \begin{pmatrix} 16 & 16 \\[1.1ex] 16 & 16 \end{pmatrix}=\begin{pmatrix} 2^4 & 2^4 \\[1.1ex] 2^4 & 2^4 \end{pmatrix}$

Oleh karena itu, kita dapat memperoleh rumus pangkat ke-n dari matriks tersebut

$A:$

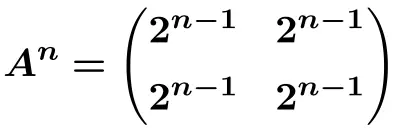
Dan dari rumus ini kita bisa menghitungnya

$A^{100}:$

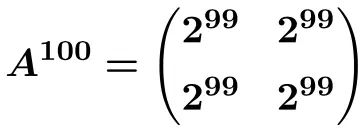
latihan diselesaikan langkah demi langkah kekuatan matriks 2x2

Memecahkan masalah daya matriks

Latihan 1

Perhatikan matriks berdimensi 2×2 berikut:

$\displaystyle A=\begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix}$

Menghitung:

$\displaystyle A^4$

lihat solusi

Untuk menghitung pangkat suatu matriks, Anda harus mengalikan matriks tersebut satu per satu. Oleh karena itu, kita hitung dulu

$\displaystyle A^2 :$

$\displaystyle A^2= A \cdot A = \begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix} = \begin{pmatrix} -1 & 4 \\[1.1ex] -2 & -1\end{pmatrix}$

Sekarang kita menghitung

$\displaystyle A^3 :$

$\displaystyle A^3= A^2 \cdot A = \begin{pmatrix} -1 & 4 \\[1.1ex] -2 & -1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix} =\begin{pmatrix} -5 & 2 \\[1.1ex] -1 & -5 \end{pmatrix}$

Dan akhirnya kami menghitung

$\displaystyle A^4 :$

$\displaystyle A^4= A^3 \cdot A = \begin{pmatrix} -5 & 2 \\[1.1ex] -1 & -5 \end{pmatrix} \cdot \begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix} = \begin{pmatrix} \bm{-7} & \bm{-8} \\[1.1ex] \bm{4} & \bm{-7} \end{pmatrix}$

Latihan 2

Perhatikan matriks orde 2 berikut:

$\displaystyle A=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix}$

Menghitung:

$\displaystyle A^{35}$

lihat solusi

$\displaystyle A^{35}$

adalah pangkat yang terlalu besar untuk dihitung dengan tangan, sehingga pangkat matriks harus mengikuti suatu pola. Jadi mari kita hitung

$\displaystyle A^5$

untuk mencoba memahami urutan yang mereka ikuti:

$\displaystyle A^2= A \cdot A = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} \cdot \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 9 \end{pmatrix}$

$\displaystyle A^3= A^2 \cdot A = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 9 \end{pmatrix} \cdot \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 27 \end{pmatrix}$

$\displaystyle A^4= A^3 \cdot A = \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 27 \end{pmatrix} \cdot \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 81 \end{pmatrix}$

$\displaystyle A^5= A^4 \cdot A = \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 81 \end{pmatrix} \cdot \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 243 \end{pmatrix}$

Dengan cara ini kita dapat melihat pola yang diikuti oleh pangkat: pada setiap pangkat, semua bilangan tetap sama, kecuali elemen pada kolom kedua pada baris kedua, yang dikalikan 3. Oleh karena itu, semua bilangan selalu tetap sama. dan elemen terakhir adalah pangkat 3:

$\displaystyle A=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^1 \end{pmatrix}$

$\displaystyle A^2=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 9 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^2 \end{pmatrix}$

$\displaystyle A^3=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 27 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^3 \end{pmatrix}$

$\displaystyle A^4=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 81 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^4 \end{pmatrix}$

$\displaystyle A^5=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 243 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^5 \end{pmatrix}$

Jadi rumus pangkat ke-n matriks

$\displaystyle A$

Timur:

$\displaystyle A^n=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^n\end{pmatrix}$

Dan dari rumus ini kita bisa menghitungnya

$\displaystyle A^{35}:$

$\displaystyle\bm{A^{35}=}\begin{pmatrix} \bm{1} & \bm{0} \\[1.1ex] \bm{0} & \bm{3^{35}}\end{pmatrix}$

Latihan 3

Perhatikan matriks 3×3 berikut:

$\displaystyle A=\begin{pmatrix} 1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Menghitung:

$\displaystyle A^{100}$

lihat solusi

$\displaystyle A^{100}$

adalah pangkat yang terlalu besar untuk dihitung dengan tangan, sehingga pangkat matriks harus mengikuti suatu pola. Jadi mari kita hitung

$\displaystyle A^5$

untuk mencoba memahami urutan yang mereka ikuti:

$\displaystyle A^2= A \cdot A = \begin{pmatrix} 1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix}1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & \frac{2}{5} & \frac{2}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\displaystyle A^3= A^2 \cdot A = \begin{pmatrix} 1 & \frac{2}{5} & \frac{2}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1\end{pmatrix} \cdot \begin{pmatrix}1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & \frac{3}{5} & \frac{3}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\displaystyle A^4= A^3 \cdot A = \begin{pmatrix} 1 & \frac{3}{5} & \frac{3}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1\end{pmatrix} \cdot \begin{pmatrix}1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & \frac{4}{5} & \frac{4}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\displaystyle A^5= A^4 \cdot A = \begin{pmatrix} 1 & \frac{4}{5} & \frac{4}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1\end{pmatrix} \cdot \begin{pmatrix}1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & \frac{5}{5} & \frac{5}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Dengan cara ini kita dapat melihat pola yang diikuti oleh pangkat: pada setiap pangkat, semua bilangan tetap sama, kecuali pecahan, yang pembilangnya bertambah satu:

$\displaystyle A=\begin{pmatrix} 1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\displaystyle A^2= \begin{pmatrix} 1 & \frac{2}{5} & \frac{2}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\displaystyle A^3= \begin{pmatrix} 1 & \frac{3}{5} & \frac{3}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\displaystyle A^4= \begin{pmatrix} 1 & \frac{4}{5} & \frac{4}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\displaystyle A^5= \begin{pmatrix} 1 & \frac{5}{5} & \frac{5}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Jadi rumus pangkat matriks ke-n

$\displaystyle A$

Timur:

$\displaystyle A^n= \begin{pmatrix} 1 & \frac{n}{5} & \frac{n}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Dan dari rumus ini kita bisa menghitungnya

$\displaystyle A^{100}:$

$\displaystyle A^{100}= \begin{pmatrix} 1 & \frac{100}{5} & \frac{100}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}= \begin{pmatrix} \bm{1} & \bm{20} & \bm{20} \\[1.1ex] \bm{0} & \bm{1} & \bm{0} \\[1.1ex] \bm{0} & \bm{0} & \bm{1} \end{pmatrix}$

Latihan 4

Perhatikan matriks berukuran 2×2 berikut:

$\displaystyle A=\begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix}$

Menghitung:

$\displaystyle A^{201}$

lihat solusi

$\displaystyle A^{201}$

adalah pangkat yang terlalu besar untuk dihitung dengan tangan, sehingga pangkat matriks harus mengikuti suatu pola. Dalam hal ini, perlu dilakukan perhitungan

$\displaystyle A^{8}$

untuk mengetahui urutan yang mereka ikuti:

$\displaystyle A^2= A \cdot A = \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix}$

$\displaystyle A^3= A^2 \cdot A = \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix}$

$\displaystyle A^4= A^3 \cdot A = \begin{pmatrix}0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} = \bm{I}$

$\displaystyle A^5= A^4 \cdot A = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1\end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix}$

$\displaystyle A^6= A^5 \cdot A = \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix}$

$\displaystyle A^7= A^6 \cdot A = \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix}$

$\displaystyle A^8= A^7 \cdot A = \begin{pmatrix}0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} = \bm{I}$

Dengan perhitungan tersebut kita dapat melihat bahwa setiap 4 pangkat kita mendapatkan matriks identitasnya. Artinya, hal ini akan memberi kita matriks identitas kekuasaan

$\displaystyle A^4$

$\displaystyle A^8$

$\displaystyle A^{12}$

$\displaystyle A^{16}$

,… Jadi untuk menghitung

$\displaystyle A^{201}$

kita harus menguraikan 201 menjadi kelipatan 4:

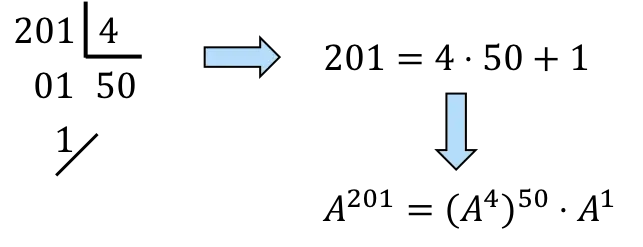
latihan diselesaikan langkah demi langkah pangkat matriks 2x2 dan pangkat n

$\displaystyle 201= 4 \cdot 50 +1$

,Belum,

$A^{201}$

itu akan menjadi 50 kali

$\displaystyle A^{4}$

dan sekali

$\displaystyle A^{1}:$

$\displaystyle A^{201}=\left(A^4 \right)^{50} \cdot A^1$

Dan bagaimana kita mengetahuinya

$\displaystyle A^4$

adalah matriks identitas

$\displaystyle I :$

$\displaystyle A^4 =I$

$\displaystyle A^{201}=\left(A^4 \right)^{50} \cdot A^1 = I^{50}\cdot A$

Selanjutnya, matriks identitas yang dipangkatkan ke sembarang bilangan menghasilkan matriks identitas. Belum:

$\displaystyle A^{201}= I^{50}\cdot A = I \cdot A$

Dan terakhir, matriks apa pun dikalikan dengan matriks identitas menghasilkan matriks yang sama. JADI:

$\displaystyle A^{201}= I \cdot A = A$

Untuk apa

$A^{201}$

adalah sama dengan

$A:$

$\displaystyle A^{201}= A =\begin{pmatrix} \bm{0} & \bm{-1} \\[1.1ex] \bm{1} & \bm{0} \end{pmatrix}$

Latihan 5

Perhatikan matriks orde 3 berikut:

$\displaystyle A=\begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix}$

Menghitung:

$\displaystyle A^{62}$

lihat solusi

Tentu saja, hitung kekuatan matriksnya

$\displaystyle A^{62}$

Perhitungan ini terlalu besar untuk dilakukan secara manual, sehingga pangkat matriks harus mengikuti suatu pola. Dalam hal ini, perlu dilakukan perhitungan

$\displaystyle A^{6}$

untuk mengetahui urutan yang mereka ikuti:

$\displaystyle A^2= A \cdot A = \begin{pmatrix}3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 3 & 3 & 1 \\[1.1ex] -2 & -2 & -1 \\[1.1ex] 0 & 1 & -1 \end{pmatrix}$

$\displaystyle A^3= A^2 \cdot A = \begin{pmatrix}3 & 3 & 1 \\[1.1ex] -2 & -2 & -1 \\[1.1ex] 0 & 1 & -1\end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\displaystyle A^4= A^3 \cdot A = \begin{pmatrix}1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix}$

$\displaystyle A^5= A^4 \cdot A = \begin{pmatrix}3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 3 & 3 & 1 \\[1.1ex] -2 & -2 & -1 \\[1.1ex] 0 & 1 & -1 \end{pmatrix}$

$\displaystyle A^6= A^5 \cdot A = \begin{pmatrix}3 & 3 & 1 \\[1.1ex] -2 & -2 & -1 \\[1.1ex] 0 & 1 & -1\end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Dengan perhitungan tersebut kita dapat melihat bahwa setiap 3 pangkat diperoleh matriks identitas. Artinya, hal ini akan memberi kita matriks identitas kekuasaan

$\displaystyle A^3$

$\displaystyle A^6$

$\displaystyle A^{9}$

$\displaystyle A^{12}$

,… Untuk menghitungnya

$\displaystyle A^{62}$

Kita harus menguraikan 62 menjadi kelipatan 3:

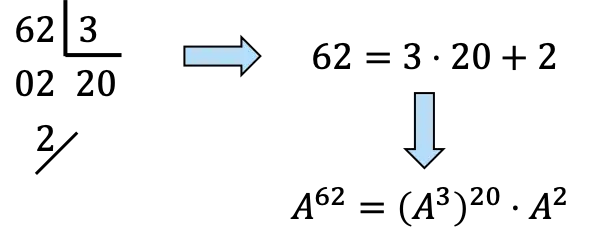
latihan diselesaikan langkah demi langkah pangkat matriks 3x3, pangkat ke-n

$\displaystyle 62= 3 \cdot 20 +2$

,Belum,

$\displaystyle A^{62}$

itu akan menjadi 20 kali

$\displaystyle A^{3}$

dan sekali

$\displaystyle A^{2}:$

$\displaystyle A^{62}=\left(A^3 \right)^{20} \cdot A^2$

Dan bagaimana kita mengetahuinya

$\displaystyle A^3$

adalah matriks identitas

$\displaystyle I :$

$\displaystyle A^3 =I$

$\displaystyle A^{62}=\left(A^3 \right)^{20} \cdot A^2 = I^{20}\cdot A^2$

Selanjutnya, matriks identitas yang dipangkatkan ke sembarang bilangan menghasilkan matriks identitas. Belum:

$\displaystyle A^{62}= I^{20}\cdot A^2 = I \cdot A^2$

Akhirnya, matriks apa pun dikalikan dengan matriks identitas menghasilkan matriks yang sama. Belum:

$\displaystyle A^{62}= I \cdot A^2 = A^2$

Untuk apa

$A^{62}$

akan sama dengan

$A^{2}$

, yang hasilnya telah kita hitung sebelumnya:

$\displaystyle A^{62}= A^2=\begin{pmatrix} \bm{3} & \bm{3} & \bm{1} \\[1.1ex] \bm{-2} & \bm{-2} & \bm{-1} \\[1.1ex] \bm{0} & \bm{1} & \bm{-1} \end{pmatrix}$

Jika latihan pangkat matriks persegi ini bermanfaat bagi Anda, Anda juga dapat menemukan latihan langkah demi langkah yang diselesaikan tentang penjumlahan dan pengurangan matriks , salah satu operasi matriks yang paling banyak digunakan.

Bagaimana cara menghitung kekuatan matriks?

Contoh penghitungan pangkat suatu matriks:

Berapakah pangkat n suatu matriks?

Contoh penghitungan pangkat n suatu matriks:

Memecahkan masalah daya matriks

Latihan 1

Latihan 2

Latihan 3

Latihan 4

Latihan 5

Tinggalkan Komentar Batalkan Balasan