Di sini kami menjelaskan cara menurunkan suatu pangkat (atau fungsi potensial), Anda akan menemukan rumus turunan suatu pangkat, beberapa contoh, dan Anda bahkan dapat berlatih dengan latihan yang diselesaikan langkah demi langkah.
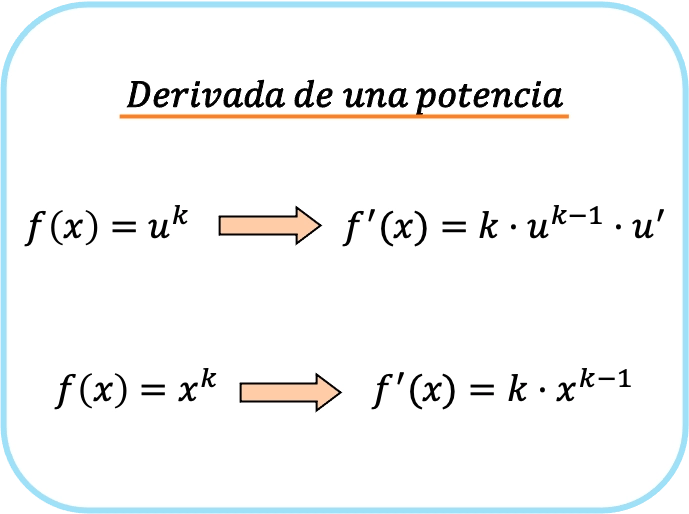
Rumus turunan suatu pangkat
Turunan suatu pangkat, atau fungsi potensial, adalah hasil kali eksponen pangkat dikalikan pangkatnya dengan pangkat dikurangi 1 kali turunan pangkatnya.
![]()
Oleh karena itu, jika basisnya adalah fungsi identitas , untuk mendapatkan pangkat, cukup kalikan fungsi tersebut dengan eksponen dan kurangi satu satuan dari eksponennya:
![]()
Memang turunan fungsi identitas sama dengan 1.
Ringkasnya, untuk menurunkan fungsi potensial, ada dua rumus: rumus pertama yang selalu dapat digunakan dan rumus kedua yang hanya dapat diterapkan jika basisnya adalah x.
Kita dapat dengan mudah memverifikasi bahwa rumus pertama yang disajikan untuk turunan suatu pangkat sama dengan rumus kedua tetapi menerapkan aturan rantai.
Perhatikan bahwa rumus ini hanya dapat digunakan jika variabelnya adalah pangkat, jika x adalah penyebutnya, Anda harus menerapkan aturan turunan fungsi eksponensial:
➤ Lihat: turunan dari fungsi eksponensial
Contoh Turunan Daya
Setelah kita melihat rumus turunan suatu fungsi potensial, kami akan menjelaskan beberapa contoh turunan jenis ini agar Anda memahami cara menurunkan pangkat.
Contoh 1: Turunan dari pangkat dasar x
![]()
Seperti yang telah kami jelaskan pada bagian sebelumnya, jika basis pangkatnya hanya x, maka rumus yang harus kita gunakan untuk menurunkan fungsinya adalah:
![]()
Oleh karena itu, turunan pangkat x yang dipangkatkan 4 adalah:
![]()
Contoh 2: Turunan suatu pangkat dengan tanda kurung
![]()
Dalam contoh ini basis bukanlah fungsi identitas, oleh karena itu kita harus menggunakan rumus umum turunan suatu pangkat:
![]()
Fungsi dalam tanda kurung merupakan fungsi linier sehingga turunannya adalah 2. Jadi, turunan seluruh fungsi potensial adalah:
![]()
Contoh 3: Turunan dari pangkat negatif
![]()
Dalam hal ini kita mempunyai fungsi potensial yang eksponennya negatif dan basisnya adalah logaritma, jadi kita akan menggunakan rumus berikut untuk membedakan fungsinya:
![]()
Sekalipun eksponen pangkatnya negatif, eksponennya juga harus dikurangkan. Oleh karena itu, turunan dari fungsi tersebut adalah:
![]()
Jika Anda ragu dengan solusinya, Anda dapat melihat rumus turunan fungsi logaritma di sini:
➤ Lihat: turunan dari fungsi logaritma
Contoh 4: Turunan dari suatu pangkat dengan akar
![]()
Fungsi dalam contoh ini adalah pangkat dalam ekspresi reguler. Namun, radikal dapat diubah menjadi ekspresi potensial, sehingga fungsinya dapat disederhanakan dengan mengubahnya menjadi fungsi potensial dengan eksponen pecahan:
![]()
Sekarang kita terapkan rumus turunan pangkat suatu variabel:
![]()
Dan turunannya adalah:
![]()
Anda juga dapat membedakan jenis fungsi ini menggunakan aturan turunan akar:
➤ Lihat: berasal dari akar kata
Latihan soal turunan suatu pangkat
Hitunglah turunan pangkat berikut:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
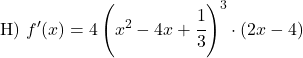
![]()