Di halaman ini Anda akan menemukan cara menghitung jarak antara dua titik dalam geometri (rumus). Anda juga akan dapat melihat contoh dan, sebagai tambahan, berlatih dengan latihan jarak antara dua titik yang telah diselesaikan.
Apa rumus jarak antara dua titik?
Jarak antara dua titik sama dengan panjang segmen yang menghubungkannya. Oleh karena itu, dalam matematika, untuk menentukan jarak antara dua titik yang berbeda, kita harus menghitung kuadrat selisih koordinatnya dan kemudian mencari akar dari jumlah kuadrat tersebut.
Dengan kata lain rumus yang digunakan untuk menghitung jarak antara dua titik berbeda pada bidang kartesius adalah sebagai berikut:
Perhatikan koordinat dua titik berbeda:
![]()
Rumus jarak antara dua titik adalah:
![]()
Rumus ini berasal dari besaran suatu vektor. Sebenarnya yang kita lakukan dengan rumus ini sebenarnya adalah menghitung besaran vektor yang ditentukan oleh dua titik yang dimaksud. Anda dapat membaca lebih lanjut mengenai hal ini pada penjelasan apa itu modulus suatu vektor .
Sebaliknya, dalam geometri analitik, demonstrasi rumus jarak antara dua titik juga dapat dilakukan dengan menggunakan teorema Pythagoras:
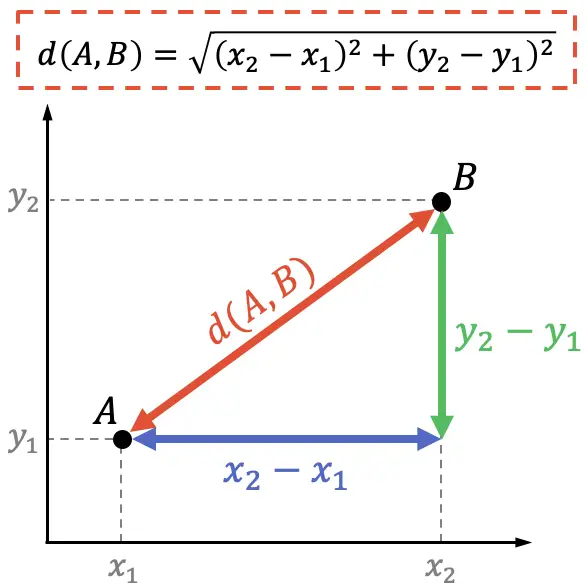
Teorema Pythagoras menyatakan bahwa kuadrat sisi miring suatu segitiga siku-siku sama dengan jumlah kuadrat kaki-kakinya, maka:
![]()
Dan untuk mendapatkan rumusnya Anda hanya perlu mencari jarak antara 2 titik tersebut:
![]()
Terakhir, perlu dicatat bahwa, jika kita bekerja dengan 3 titik koordinat, rumus jarak antara dua titik dalam ruang (dalam R3) akan sama tetapi menambahkan koordinat Z:
![]()
Contoh penghitungan jarak antara dua titik
Setelah kita melihat definisi rumus jarak antara dua titik, sekarang mari kita lihat cara menentukan jarak tersebut dengan menggunakan contoh:
- Tentukan jarak antara dua titik berikut:
![]()
Untuk mencari jarak antara dua titik secara geometris, cukup terapkan rumus:
![]()
Sekarang kita substitusikan koordinat titik-titik tersebut ke dalam rumus:
![]()
Dan kami melakukan perhitungan:
![Rendered by QuickLaTeX.com \begin{aligned} d(A,B) &= \sqrt{(3+1)^2+(4-7)^2 \vphantom{\frac{1}{2}}} \\[2ex] &= \sqrt{4^2+(-3)^2 \vphantom{\frac{1}{2}}} \\[2ex] &= \sqrt{16+9}\\[2ex] &= \sqrt{25}\\[2ex] & = \bm{5}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4e48600907e65f89fb9be0d55a2d3b3a_l3.png)
Oleh karena itu, jarak antara dua titik sama dengan 5 satuan.
Tentunya nilai jarak harus selalu memberikan tanda positif, karena jarak selalu positif. Jika tidak, berarti kita melakukan kesalahan dalam satu langkah.
Mengatasi masalah jarak antara dua titik
Latihan 1
Hitunglah jarak antara dua titik berikut:
![]()
Untuk mencari jarak geometri antara dua titik, cukup gunakan rumus:
![]()
Sekarang kita substitusikan koordinat titik-titik tersebut ke dalam rumus:
![]()
Dan kami melakukan perhitungan:
![Rendered by QuickLaTeX.com \begin{aligned} d(A,B) & = \sqrt{(-3)^2+3^2 } \\[2ex] & = \sqrt{9+9 } \\[2ex] & = \bm{\sqrt{18}} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-81d70676cabdc2985f2ebe7b88c54e2d_l3.png)
Latihan 2
Tentukan jarak antara dua titik berikut:
![]()
Untuk mencari jarak matematis antara dua titik, kita harus menggunakan rumus yang sesuai:
![]()
Sekarang kita substitusikan koordinat titik-titik tersebut ke dalam rumus:
![]()
Dan kami melakukan perhitungan:
![Rendered by QuickLaTeX.com \begin{aligned} d(A,B) &= \sqrt{(-12)^2+(-5)^2 } \\[2ex] &= \sqrt{144+25 }\\[2ex] &= \sqrt{169} \\[2ex] &= \bm{13}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1c9f9f5c93377868a352891d5b09630a_l3.png)
Latihan 3
Hitung keliling segitiga yang dibentuk oleh titik A, B dan C seperti terlihat pada grafik di bawah ini:
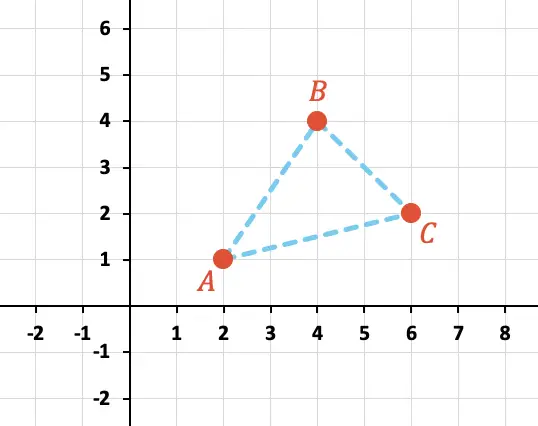
Pertama, kita perlu mengidentifikasi koordinat X dan Y setiap titik pada grafik:
![]()
![]()
![]()
Dan sekarang kita perlu menghitung jarak antara semua titik dengan rumus:
![]()
![]()
![]()
Jadi keliling segitiga sama dengan jumlah panjang ketiga sisinya:
![]()
Latihan 4
Periksa apakah segitiga yang titik sudutnya adalah titik A, B, dan C merupakan segitiga sama kaki. Tapi tiga poin:
![]()
Agar segitiga sama kaki, dua sisinya harus sama panjang. Oleh karena itu, kita harus mencari panjang masing-masing sisinya, yang sesuai dengan jarak antara titik sudutnya.
Oleh karena itu kami menghitung jarak antara titik sudut segitiga:
![]()
![]()
![]()
Jadi segitiga tersebut mempunyai 2 sisi yang identik dan ukuran sisi ketiganya berbeda dari dua sisi lainnya, maka segitiga tersebut sebenarnya merupakan segitiga sama kaki.
Latihan 5
Temukan sebuah titik pada sumbu Y yang berjarak sama dari dua titik berikut:
![]()
Pertama-tama, jika suatu titik terletak pada sumbu komputer (sumbu OY) berarti absis titik tersebut adalah nol:
![]()
Kedua, jika titik tersebut berjarak sama dari titik A dan B, maka persamaan berikut terpenuhi:
![]()
Jadi, dengan menggunakan rumus jarak antara dua titik, kita dapat mencari nilai variabel y dari persamaan sebelumnya:
![]()
Karena kedua ruas persamaan mempunyai akar, kita dapat menyederhanakannya:
![]()
Kami menyelesaikan kekuatan dan persamaan penting (atau produk penting):
![]()
Dan kami beroperasi sampai kami menemukan nilai yang tidak diketahui y :
![]()
![]()
![]()
![]()
Singkatnya, poin dari pernyataan masalah yang ditanyakan kepada kami adalah:
![]()
Jika Anda merasa artikel ini bermanfaat, Anda mungkin juga tertarik dengan latihan jarak antara titik dan garis . Pada halaman tertaut Anda tidak hanya akan menemukan latihan yang diselesaikan selangkah demi selangkah, tetapi juga penjelasan rinci tentang menghitung jarak antara titik dan garis, contoh dan penerapan rumus jarak antara titik dan garis untuk menentukan jenis jarak lainnya. .