Di sini Anda akan menemukan rumus semua jenis persamaan garis. Selain itu, Anda akan dapat melihat contoh cara menghitungnya dan, sebagai tambahan, berlatih dengan latihan persamaan garis yang telah diselesaikan.
Apa saja persamaan garisnya?
Ingatlah bahwa definisi matematis garis adalah sekumpulan titik berurutan yang direpresentasikan dalam arah yang sama tanpa kurva atau sudut.
Jadi, untuk menyatakan secara analitis setiap garis lurus pada bidang (dalam R2) kita menggunakan persamaan garis lurus, dan untuk menemukannya Anda hanya memerlukan sebuah titik yang termasuk dalam garis lurus tersebut dan vektor arah dari garis lurus tersebut. Hanya dengan dua elemen geometri ini, Anda dapat menemukan semua persamaan garis yang berbeda, yaitu sebagai berikut:
Persamaan garis adalah persamaan vektor, persamaan parametrik, persamaan kontinu, persamaan implisit (atau umum), persamaan eksplisit, persamaan titik-kemiringan, dan persamaan kanonik (atau segmental).
Semua jenis persamaan garis memiliki tujuan yang sama: merepresentasikan garis secara matematis. Tetapi setiap persamaan garis mempunyai sifat-sifatnya masing-masing dan oleh karena itu, tergantung pada masalahnya, lebih baik menggunakan salah satu persamaan tersebut.

Setelah kita melihat konsep persamaan garis, sekarang kita beralih ke analisis karakteristik masing-masing jenis persamaan garis secara khusus. Di bawah ini Anda memiliki penjelasan rinci tentang berbagai jenis persamaan pada garis, tetapi jika mau, Anda dapat langsung menuju ke akhir tabel ringkasan dengan rumus semua persamaan pada garis .
Persamaan vektor garis
Ya
![]()
adalah vektor arah garis dan
![]()
suatu titik yang berada di sebelah kanan:
![]()
Rumus persamaan vektor garis adalah:
![]()
Emas:
-

Dan

adalah koordinat kartesius dari setiap titik pada garis.
-

Dan

adalah koordinat suatu titik yang diketahui membentuk bagian garis

-

Dan

adalah komponen vektor arah garis

-

adalah skalar (bilangan real) yang nilainya bergantung pada setiap titik pada garis.
Ini adalah persamaan vektor garis pada bidang, yaitu ketika bekerja dengan titik dan vektor 2 koordinat (dalam R2). Namun, jika kita melakukan perhitungan dalam ruang (dalam R3), kita harus menambahkan komponen tambahan pada persamaan garis:
![]()
Persamaan parametrik garis
Persamaan parametrik suatu garis dapat diperoleh dari persamaan vektornya:
![]()
Kita kalikan dulu parameternya
![]()
dengan vektor arah ke kanan:
![]()
Selanjutnya kita tambahkan koordinat X dan Y:
![]()
Dan, terakhir, dengan membersihkan setiap variabel secara terpisah, kita memperoleh persamaan parametrik garis:
![]()
Emas:
-

Dan

adalah koordinat Cartesius dari setiap titik pada garis.
-

Dan

adalah koordinat suatu titik yang diketahui membentuk bagian garis

-

Dan

adalah komponen vektor arah garis

-

adalah skalar (bilangan real) yang nilainya bergantung pada setiap titik pada garis.
Seperti sebelumnya, berikut adalah persamaan parametrik garis pada bidang (dalam R2), namun untuk mencari persamaan parametrik garis dalam ruang (dalam R3) perlu ditambahkan satu persamaan lagi untuk variabel ketiga Z:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \\[1.7ex] z=P_3+t\cdot\text{v}_3\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e31f05449ce57a8af9ae4dda38535013_l3.png)
Persamaan garis kontinu
Persamaan kontinu suatu garis dapat disimpulkan dari persamaan parametriknya:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-708dbb33878e2bab0dcc94c84f6ab670_l3.png)
Jika kita menghapus pengaturannya
![]()
dari setiap persamaan parametrik kita memperoleh ekspresi berikut:
![]()
![]()
E Dengan menyamakan kedua persamaan yang dihasilkan, kita memperoleh persamaan garis kontinu:
![]()
![]()
Singkatnya, persamaan garis kontinu adalah:
![]()
Emas:
-

Dan

adalah koordinat Cartesius dari setiap titik pada garis.
-

Dan

adalah koordinat suatu titik yang diketahui membentuk bagian garis

-

Dan

adalah komponen vektor arah garis

Rumus ini untuk persamaan garis kontinu bila dikerjakan dalam 2 dimensi (dalam 2D). Namun jika kita melakukan operasi dalam 3 dimensi (3D), kita perlu menambahkan komponen tambahan pada persamaan garis:
![]()
Persamaan garis implisit atau umum
Ya
![]()
adalah vektor arah garis dan
![]()
suatu titik yang berada di sebelah kanan:
![]()
Rumus persamaan garis implisit, umum atau kartesius adalah:
![]()
Emas:
-

Dan

adalah koordinat Cartesius dari setiap titik pada garis.
- koefisien

adalah komponen kedua dari vektor arah garis:

- koefisien

adalah komponen pertama dari tanda perubahan vektor arah:

- koefisien

dihitung dengan mengganti titik yang diketahui

dalam persamaan garis.
rumusnya, persamaan implisit suatu garis juga dapat diperoleh dengan mengalikan pecahan persamaan kontinu tersebut.
Persamaan garis eksplisit
Rumus persamaan garis eksplisit adalah:
![]()
Emas:
-

adalah kemiringan garis.
-

perpotongannya dengan sumbu Y, yaitu ketinggian perpotongannya dengan sumbu Y.
Pada bagian di bawah ini Anda akan melihat bagaimana parameter ditentukan
![]()
Dan
![]()
dari garis lurus Namun, khususnya, cara lain untuk mencari persamaan eksplisit adalah dengan menggunakan persamaan implisit; untuk ini, hal yang tidak diketahui harus diselesaikan
![]()
dari persamaan implisit.
Arti parameter m dan n
Seperti yang kita lihat pada definisi persamaan garis eksplisit, parameter
![]()
adalah kemiringan garis dan
![]()
perpotongan y-nya. Tapi apa maksudnya? Mari kita lihat ini dari representasi grafis sebuah garis:

Istilahnya mandiri
![]()
adalah titik potong garis dengan sumbu komputer (sumbu OY). Misalnya pada grafik di atas
![]()
sama dengan 1 karena garis tersebut memotong sumbu y di y=1.
Di sisi lain, istilahnya
![]()
menunjukkan kemiringan garis , yaitu kemiringannya. Seperti yang Anda lihat pada grafik,
![]()
sama dengan 2 karena garis naik 2 satuan vertikal untuk 1 satuan horizontal.
Jelasnya, jika kemiringannya positif maka fungsinya bertambah (naik), sebaliknya jika kemiringannya negatif maka fungsinya menurun (turun).
Menghitung kemiringan suatu garis
Setelah kita mengetahui secara pasti kemiringan suatu garis, mari kita lihat cara menghitungnya. Jadi, ada 3 cara berbeda untuk menentukan kemiringan suatu garis secara numerik:
- Diberikan dua titik berbeda pada garis tersebut

Dan

Kemiringan garis sama dengan:
- Ya

adalah vektor arah garis, kemiringannya adalah:
- Ya

adalah sudut yang dibentuk oleh garis dengan sumbu absis (sumbu X), kemiringan garis tersebut ekuivalen dengan garis singgung sudut tersebut:
![]()
![]()
![]()

Persamaan titik-kemiringan garis
Rumus persamaan titik-kemiringan garis adalah:
![]()
Emas:
-

adalah kemiringan garis.
-

adalah koordinat suatu titik pada garis

Persamaan garis kanonik atau segmental
Meskipun varian persamaan garis ini kurang dikenal, persamaan garis kanonik dapat diperoleh dari titik potong garis dengan sumbu kartesius.
Misalkan dua titik potong dengan sumbu suatu garis adalah:
Potong dengan sumbu X:
![]()
Potong dengan sumbu Y:
![]()
Rumus persamaan garis kanonik adalah:
![]()

Dalam matematika, persamaan garis kanonik disebut juga persamaan segmental atau persamaan simetris.
Di sisi lain, koefisien
![]()
Dan
![]()
Mereka juga dapat dicari dari persamaan garis umum dengan menggunakan rumus berikut:
![]()
![]()
Semua persamaan garis (rumus)
Ringkasnya, berikut adalah tabel yang menunjukkan rumus semua persamaan garis:

Contoh penghitungan persamaan garis
Sekarang kita telah melihat penjelasan keseluruhan tentang persamaan garis, mari kita lihat bagaimana suatu masalah umum persamaan garis diselesaikan:
- Temukan semua persamaan garis yang ditentukan oleh titik tersebut

dan vektornya
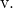
![]()
Pertama-tama kita cari persamaan vektor garis dari rumusnya:
![]()
Cukup substitusikan koordinat titik dan vektor ke dalam rumus:
![]()
Kedua, kita menemukan persamaan parametrik garis melalui rumus yang sesuai:
![Rendered by QuickLaTeX.com \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d2e6878c4d9b80337639f5fa7728a9f9_l3.png)
![Rendered by QuickLaTeX.com \definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=3+2t} \\[1.7ex] \bm{y=-1+4t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }](https://mathority.org/wp-content/ql-cache/quicklatex.com-3b4690a2ab033a4016f2d16b9554ddea_l3.png)
Dan kita juga menentukan persamaan garis kontinu dengan rumusnya :
![]()
![]()
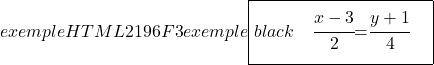
Seperti yang Anda lihat, persamaan vektor, parametrik, dan kontinu mudah dihitung, Anda hanya perlu menggunakan rumusnya masing-masing.
Sekarang mari kita beralih ke mencari persamaan garis umum (atau implisit). Untuk melakukan ini, kita menyilangkan dua pecahan dari persamaan kontinu:
![]()
![]()
![]()
![]()
Sekarang kita dapat menentukan persamaan eksplisit penyelesaian garis untuk hal yang tidak diketahui
![]()
dari persamaan implisit:
![]()
![]()
![]()
![]()
Oleh karena itu, kemiringan garis tersebut sama dengan 2 (suku yang menyertai variabel bebas
![]()
).
![]()
Dan dengan ini kita dapat menghitung persamaan titik-kemiringan garis dengan rumusnya:
![]()
![]()
![]()
Terakhir, untuk mencari persamaan segmental garis tersebut kita hitung titik potongnya dengan sumbu OX dan OY kemudian kita terapkan rumusnya:
![]()
Titik potong dengan sumbu absis (sumbu X)
![]()
![]()
![]()
![]()
![]()
Titik potong dengan sumbu y (sumbu Y)
![]()
![]()
![]()
![]()
![]()
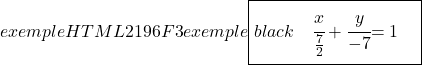
persamaan garis lurus yang melalui dua titik
Masalah umum lainnya dalam persamaan garis adalah mencari persamaan garis yang ditentukan oleh dua titik tertentu. Meskipun kita dapat menghitung vektor arah garis dengan 2 titik dan kemudian persamaannya, di bawah ini kami berikan rumus yang dapat digunakan untuk mencari persamaan garis tersebut secara langsung dan mudah.
Perhatikan dua titik yang terletak pada sebuah garis:
![]()
Rumus mencari persamaan garis dari 2 titiknya adalah:
![]()
Rumus ini memungkinkan kita menghitung secara langsung persamaan titik-kemiringan garis ketika kita diberikan 2 titik yang dilalui garis tersebut.
Menyelesaikan masalah persamaan garis
Latihan 1
Temukan persamaan vektor, persamaan parametrik, dan persamaan kontinu garis yang dibatasi oleh titik
![]()
dan vektor pengarahnya
![]()
Jadilah keduanya:
![]()
Pertama, kita menghitung persamaan vektor garis dari rumusnya:
![]()
![]()
Kami kemudian menemukan persamaan parametrik garis menggunakan rumus yang sesuai:
![Rendered by QuickLaTeX.com \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d2e6878c4d9b80337639f5fa7728a9f9_l3.png)
![Rendered by QuickLaTeX.com \begin{cases} x=0+t\cdot (-1) \\[1.7ex] y=3+t\cdot 5\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a734c32ae40ca816c19b895e54916eb4_l3.png)
![Rendered by QuickLaTeX.com \definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=-t} \\[1.7ex] \bm{y=3+5t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }](https://mathority.org/wp-content/ql-cache/quicklatex.com-bff16cf5ab85c87d8a866a2d74ea2a31_l3.png)
Dan terakhir, kita menentukan persamaan garis kontinu dengan rumusnya masing-masing:
![]()
![]()
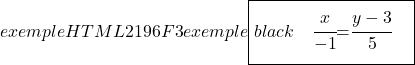
Latihan 2
Temukan persamaan implisit, persamaan eksplisit, dan persamaan titik-kemiringan garis yang ditentukan oleh titik tersebut
![]()
dan vektor arahnya adalah
![]()
![]()
Rumus persamaan garis implisit adalah:
![]()
Oleh karena itu kita harus mencari koefisien A, B dan C. Yang tidak diketahui A dan B diperoleh dari koordinat vektor arah garis, karena persamaan berikut selalu dibuktikan:
![]()
Oleh karena itu, koefisien A adalah koordinat kedua vektor, dan koefisien B adalah koordinat pertama vektor yang diubah tandanya:
![Rendered by QuickLaTeX.com \left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}= (2,6) \end{array} \right\}\longrightarrow \begin{array}{l}A=6 \\[2ex] B=-2 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9357fbcba6acde824f0fa1cc3e389a0c_l3.png)
Oleh karena itu, kita hanya perlu mencari koefisien C. Untuk melakukannya, kita harus mensubstitusikan titik yang kita ketahui termasuk dalam garis ke dalam persamaannya:
![]()
![]()
![]()
![]()
![]()
Jadi persamaan garis implisit, umum atau kartesius adalah:
![]()
Sekarang kita dapat menentukan persamaan eksplisit penyelesaian garis untuk hal yang tidak diketahui
![]()
dari persamaan implisit:
![]()
![]()
![]()
![]()
Oleh karena itu, kemiringan garisnya sama dengan 3 (suku sebelum variabel bebas
![]()
).
![]()
Dan dari nilai kemiringan garis tersebut kita dapat menghitung persamaan titik-kemiringan garis dengan rumusnya:
![]()
![]()
![]()
Latihan 3
Tentukan 3 titik pada garis berikut, yang dinyatakan sebagai persamaan implisit atau umum:
![]()
Untuk menghitung suatu titik pada suatu garis, kita hanya perlu memberikan nilai pada salah satu variabel dan kemudian mencari nilai variabel lainnya pada titik tersebut.
Kami menghitung poin pertama dengan melakukan
![]()
![]()
![]()
![]()
![]()
![]()
Kami kemudian menemukan titik kedua yang memberikan nilai lain pada variabel tersebut
![]()
Misalnya
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Dan terakhir, kami menghitung poin ketiga dengan menyelesaikannya
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Latihan 4
Temukan semua persamaan garis yang ditentukan oleh titik
![]()
dan vektornya
![]()
![]()
Pertama-tama kita cari persamaan vektor garis dari rumusnya:
![]()
![]()
Kedua, kita menemukan persamaan parametrik garis melalui rumus yang sesuai:
![Rendered by QuickLaTeX.com \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d2e6878c4d9b80337639f5fa7728a9f9_l3.png)
![Rendered by QuickLaTeX.com \definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=-1-3t} \\[1.7ex] \bm{y=4+6t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }](https://mathority.org/wp-content/ql-cache/quicklatex.com-f3bf46da9a68147118874a619f918077_l3.png)
Dan kita juga menentukan persamaan garis kontinu dengan menggunakan rumusnya:
![]()
![]()
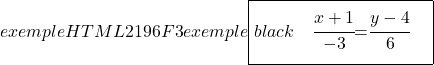
Sekarang mari kita beralih ke mencari persamaan garis implisit atau umum. Untuk melakukan ini, kita menyilangkan dua pecahan dari persamaan kontinu:
![]()
![]()
![]()
![]()
Sekarang kita dapat menentukan persamaan eksplisit penyelesaian garis untuk hal yang tidak diketahui
![]()
dari persamaan implisit:
![]()
![]()
![]()
![]()
Oleh karena itu, kemiringan garis tersebut setara dengan -2 (suku yang menyertai variabel bebas
![]()
).
![]()
Dan dengan ini kita dapat menghitung persamaan titik-kemiringan garis dengan rumusnya:
![]()
![]()
![]()
Terakhir, untuk mencari persamaan segmen garis, kita hitung titik potong garis dengan sumbu OX dan OY kemudian kita gunakan rumusnya:
![]()
Titik potong dengan sumbu absis (sumbu X)
![]()
![]()
![]()
![]()
![]()
Titik potong dengan sumbu y (sumbu Y)
![]()
![]()
![]()
![]()
![]()
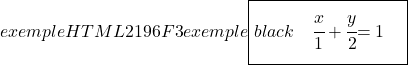
Latihan 5
Tentukan persamaan garis yang melalui dua titik berikut:
![]()
Karena kita sudah mengetahui dua titik pada garis, maka kita langsung menerapkan rumus persamaan garis pada 2 titik tertentu:
![]()
Sekarang kita substitusikan koordinat Cartesian titik-titik tersebut ke dalam rumus:
![]()
Dan terakhir, kita menghitung kemiringan garis:
![]()
![]()
Maka persamaan garis yang melalui kedua titik tersebut adalah:
![]()