▷ Tingkat perubahan rata-rata dan seketika (latihan terselesaikan)

Di sini kami menjelaskan apa yang dimaksud dengan laju perubahan, laju perubahan rata-rata, dan laju perubahan sesaat. Anda akan dapat melihat beberapa contoh tentang cara menghitung laju perubahan dan, sebagai tambahan, Anda akan dapat berlatih dengan latihan langkah demi langkah yang telah diselesaikan mengenai laju perubahan.

Berapa tingkat perubahannya?

Dalam matematika, laju perubahan (TV) suatu fungsi adalah selisih nilai suatu fungsi pada dua titik yang berbeda. Oleh karena itu, untuk menghitung laju perubahan antara dua titik, nilai fungsi pada kedua titik tersebut harus dikurangi.

$\text{TV}[a,b]=f(b)-f(a)$

Misalnya, jika dua bayangan suatu fungsi adalah f(2)=1 dan f(5)=7, laju perubahannya adalah:

$\text{TV}[2,5]=f(5)-f(2)=7-1=6$

Kita baru saja melihat arti matematis dari laju perubahan, namun dalam ilmu ekonomi konsep laju perubahan memiliki arti sebagai berikut:

Dalam ilmu ekonomi, laju perubahan antara dua nilai adalah selisih keduanya yang dinyatakan dalam persentase, yaitu laju perubahan suatu variabel antara periode yang berbeda adalah perubahan relatifnya. Oleh karena itu, untuk menghitung laju perubahan, nilai kedua periode yang berbeda dikurangkan dan hasil yang diperoleh dibagi dengan nilai periode awal.

$\text{TV}[t,t+n]=\cfrac{Y_{t+n}-Y_t}{Y_t}\cdot 100$

Misalnya, jika nilai saham tertentu meningkat dari €35 menjadi €50 dalam satu bulan, tingkat perubahannya adalah:

$\text{TV}[t,t+1]=\cfrac{50-35}{35}\cdot 100=42,86 \ \%$

Mengingat dua kemungkinan arti laju perubahan, dalam artikel ini kita akan fokus pada pemahaman definisi matematis laju perubahan. Dua jenis laju perubahan dapat dibedakan: laju perubahan rata-rata dan laju perubahan sesaat. Di bawah ini Anda memiliki penjelasan masing-masing jenisnya.

Tingkat perubahan rata-rata

Laju perubahan rata-rata (TVM) suatu fungsi dalam suatu interval adalah banyaknya satuan kenaikan (atau penurunan) fungsi tersebut untuk setiap satuan kenaikan variabel bebasnya. Oleh karena itu, laju perubahan rata-rata suatu fungsi dihitung dengan membagi pertumbuhan fungsi dalam suatu interval dengan amplitudo interval yang sama.

$\text{TVM}[a,b]=\cfrac{f(b)-f(a)}{b-a}$

Agar Anda dapat melihat cara menghitung tingkat perubahan rata-rata, kami telah menyelesaikan contoh langkah demi langkah di bawah ini.

Contoh penghitungan rata-rata laju perubahan suatu fungsi

Hitung laju perubahan rata-rata pada interval [2.5] dari fungsi berikut:

$f(x) = x^2-1$

Pertama, kita menghitung nilai fungsi pada x=2 dan x=5:

$f(5)= 5^2-1=25-1=24$

$f(2)=2^2-1=4-1=3$

Dan kemudian kita menghitung laju rata-rata perubahan fungsi dalam interval hanya dengan menerapkan rumus:

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [2,5]=\cfrac{f(5)-f(2)}{5-2} = \cfrac{24 - 3}{5-2} = \cfrac{21}{3} = \bm{7}$

Karena hasil TVM[2,5] positif, berarti fungsi tersebut bertambah pada interval [2,5]. Sebaliknya, jika hasilnya negatif, berarti fungsinya menurun pada interval tersebut.

Interpretasi geometris dari tingkat perubahan rata-rata

Secara geometris, laju perubahan rata-rata suatu fungsi dalam suatu interval menyatakan kemiringan garis yang menghubungkan titik-titik ekstrem pada interval tersebut.

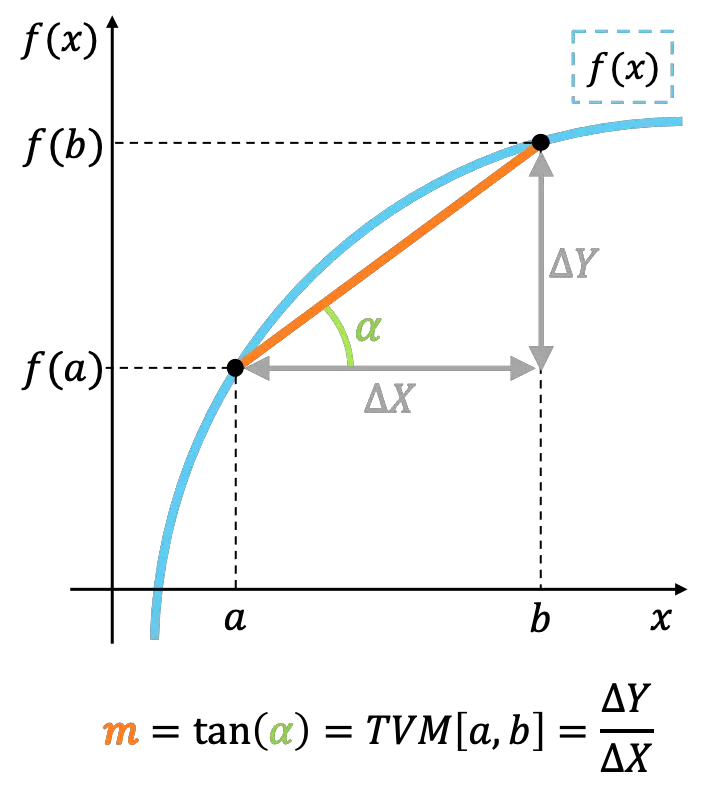
Tingkat perubahan seketika

Laju perubahan sesaat (TVI) suatu fungsi pada suatu titik adalah batas kenaikan relatif fungsi tersebut pada suatu interval yang sangat kecil. Oleh karena itu, laju perubahan sesaat dihitung dengan menyelesaikan limit hasil bagi f(a+h)-f(a) dengan h mendekati nol.

$\displaystyle\text{TVI}(a)=\lim_{h \to 0}\frac{f(a+h)-f(a)}{h}$

Nilai laju perubahan sesaat dapat bernilai positif, negatif, atau nol, yang berarti fungsi pada titik tersebut masing-masing meningkat, menurun, atau tetap sama pada titik tersebut.

Contoh penghitungan laju perubahan sesaat suatu fungsi

Hitung laju perubahan sesaat di titik x=2 dari fungsi berikut:

$f(x) = x^2$

Untuk menghitung laju perubahan sesaat, kita perlu menerapkan rumus:

$\text{TVI} (a) = \lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h} = \lim\limits_{h \to 0} \cfrac{(2+h)^2-2^2}{h}$

Kami menyelesaikan identitas penting:

$\lim\limits_{h \to 0} \cfrac{2^2+h^2+2\cdot 2 \cdot h -2^2}{h} = \lim\limits_{h \to 0} \cfrac{4+h^2+4h -4}{h} = \lim\limits_{h \to 0} \cfrac{h^2+4h}{h}$

➤ Jika Anda tidak ingat lagi rumus identitas penting , Anda akan menemukan semua rumus di situs kami yang mengkhususkan diri pada polinomial: www.polinomios.org

Sekarang mari kita coba menyelesaikan limitnya:

$\lim\limits_{h \to 0} \cfrac{h^2+4h}{h} = \cfrac{0^2+4\cdot 0}{0} =\cfrac{0}{0}$

Tapi kami menemukan nol ketidakpastian antara nol, oleh karena itu:

$\lim\limits_{h \to 0} \cfrac{h^2+4h}{h}= \lim\limits_{h \to 0} \cfrac{\cancel{h}(h+4)}{\cancel{h}} = \lim\limits_{h \to 0} (h+4)$

➤ Lihat: cara menyelesaikan limit dengan ketidakpastian nol di antara nol

Dan akhirnya kami memecahkan batasnya:

$\lim\limits_{h \to 0} (h+4) = 0 +4 = \bm{4}$

Belum:

$\mathbf{TVI} \bm{(2) = 4}$

Karena hasil TVI(2) positif, berarti fungsinya bertambah pada x=2. Sebaliknya jika hasilnya negatif berarti fungsinya sedang menurun pada tahap ini.

Interpretasi geometris dari laju perubahan sesaat

Secara geometris, laju perubahan sesaat suatu fungsi di suatu titik menyatakan kemiringan garis singgung fungsi tersebut di titik yang sama.

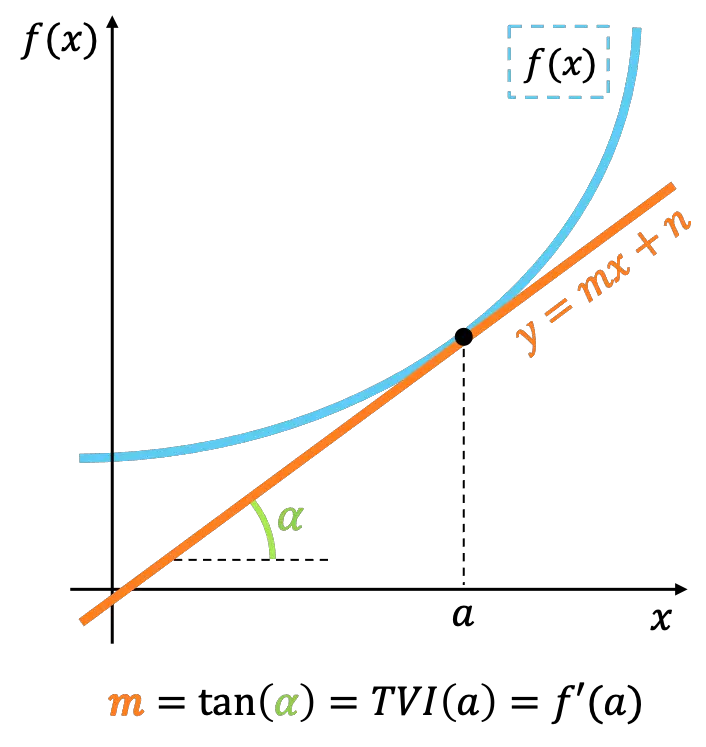
Jika dicermati, pengertian laju perubahan sesaat setara dengan konsep turunan suatu fungsi . Jadi, laju perubahan sesaat juga digunakan untuk menghitung nilai turunan suatu fungsi di suatu titik.

Latihan terpecahkan tentang tingkat perubahan

Latihan 1

Hitung nilai laju perubahan fungsi berikut pada interval [1,3].

$f(x)=x^2-5$

Lihat solusinya

Pertama, kita tentukan nilai fungsi di ujung interval:

$f(1)=1^2-5=1-5=-4$

$f(3)=3^2-5=9-5=4$

Dan sekarang kita menerapkan rumus laju perubahan:

$\text{TV}[a,b]=f(b)-f(a)$

$\text{TV}[1,3]=f(3)-f(1)=4-(-4)=4+4=\bm{8}$

Latihan 2

Hitung laju perubahan rata-rata (TVM) dari fungsi berikut selama interval [1,4]:

$f(x)=2x+1$

Lihat solusinya

Pertama kita hitung dulu gambaran fungsi di x=1 dan x=4.

$f(4)=2\cdot4+1=9$

$f(1)=2\cdot 1+1=3$

Dan kami menerapkan rumus untuk tingkat perubahan rata-rata:

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [1,4] = \cfrac{f(4)-f(1)}{4-1} = \cfrac{9-3}{4-1}=\cfrac{6}{3} = \bm{2}$

Latihan 3

Temukan laju rata-rata perubahan fungsi berikut dalam interval [-1.3]:

$f(x)=(x+1)^2$

Lihat solusinya

Untuk menentukan laju perubahan rata-rata, pertama-tama kita perlu menghitung f(-1) dan f(3):

$f(3)=(3+1)^2=(4)^2=16$

$f(-1)=((-1)+1)^2=(0)^2=0$

Kami sekarang menggunakan rumus untuk tingkat perubahan rata-rata:

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [-1,3] = \cfrac{f(3)-f(-1)}{3-(-1)} = \cfrac{16-0}{3+1}=\cfrac{16}{4} = \bm{4}$

Latihan 4

Hitung rata-rata laju perubahan pada interval [2,4] dari fungsi yang ditunjukkan pada grafik berikut:

Lihat solusinya

Kami menerapkan rumus untuk tingkat perubahan rata-rata:

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [2,4]=\cfrac{f(4)-f(2)}{4-2}$

Seperti yang kita lihat di rumus, kita perlu mencari nilai f(4) dan f(2). Dan ini dapat dengan mudah dilakukan dengan melihat representasi grafis dari fungsi tersebut:

$f(4)=5$

$f(2)=1$

Dan sekarang setelah kita mengetahui nilai fungsinya, kita substitusikan ke dalam rumus:

$\text{TVM}[2,4]=\cfrac{f(4)-f(2)}{4-2}=\cfrac{5-1}{4-2}=\cfrac{4}{2}=\bm{2}$

Latihan 5

Hitung laju perubahan sesaat fungsi berikut di titik x=2:

$f(x)=3x$

Lihat solusinya

Untuk menentukan laju perubahan fungsi sesaat di titik x=2 kita menerapkan rumus yang sesuai:

$\text{TVI}(a)=\lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\begin{array}{l}\text{TVI}(2)=\lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}=\\[4ex]=\lim\limits_{h \to 0} \cfrac{3(2+h)-3\cdot 2}{h} =\\[4ex]=\lim\limits_{h \to 0} \cfrac{6+3h-6}{h}= \lim\limits_{h \to 0} \cfrac{3h}{h} =\\[4ex]=\lim\limits_{h \to 0} \cfrac{3\cancel{h}}{\cancel{h}}=\lim\limits_{h \to 0} 3 = \bm{3}\end{array}$

Latihan 6

Tentukan laju perubahan sesaat (TVI) dari fungsi berikut di titik x=1:

$f(x)=x^2+1$

Lihat solusinya

Kami menerapkan rumus untuk laju perubahan sesaat:

$\text{TVI} (a) = \lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\text{TVI} (1) = \lim\limits_{h \to 0} \cfrac{f(1+h)-f(1)}{h}$

Lalu, kami menghitung

$f(1+h)$

Dan

$f(1):$

$f(1+h) = (1+h)^2+1$

$f(1)=1^2+1=1+1=2$

Dan kami mengganti nilai yang ditemukan dalam batasnya:

$\text{TVI} (1) = \lim\limits_{h \to 0} \cfrac{f(1+h)-f(1)}{h}= \lim\limits_{h \to 0} \cfrac{(1+h)^2+1-2}{h} =\lim\limits_{h \to 0} \cfrac{(1+h)^2-1}{h}$

Kami memecahkan produk penting:

$\lim\limits_{h \to 0} \cfrac{1^2+h^2+2\cdot 1 \cdot h-1}{h}=\lim\limits_{h \to 0} \cfrac{1+h^2+2h-1}{h}=\lim\limits_{h \to 0} \cfrac{h^2+2h}{h}$

Sekarang mari kita coba menyelesaikan limitnya:

$\lim\limits_{h \to 0} \cfrac{h^2+2h}{h}=\cfrac{0^2+2\cdot 0}{0} = \cfrac{0}{0}$

Tapi kita menemukan bentuk tak tentu nol dibagi nol, jadi kita memfaktorkan polinomial pembilang pecahan dan menyederhanakannya:

$\lim\limits_{h \to 0} \cfrac{h^2+2h}{h}=\lim\limits_{h \to 0} \cfrac{h(h+2)}{h} = \lim\limits_{h \to 0} \cfrac{\cancel{h}(h+2)}{\cancel{h}}= \lim\limits_{h \to 0}(h+2)$

➤ Jika anda belum mengetahui cara menyelesaikan zero indeterminacy between zero , penjelasan selengkapnya dapat anda lihat pada link diatas tentang cara menyelesaikan limit dengan zero indeterminacy antara nol.

Dan akhirnya, kami menyelesaikan batasannya:

$\lim\limits_{h \to 0}(h+2) = 0+2 =\bm{2}$

Ringkasnya, laju perubahan fungsi sesaat di titik x=1 sama dengan 2.

$\mathbf{TVI} \bm{(1) = 2}$

Latihan 7

Tentukan laju perubahan sesaat fungsi berikut di titik x=2:

$f(x)=4x^2-x+3$

Lihat solusinya

Pertama-tama kita menggunakan rumus laju perubahan sesaat:

$\text{TVI} (a) = \lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}$

Kami menghitung

$f(2+h)$

Dan

$f(2):$

$f(2+h) = 4(2+h)^2-(2+h)+3=4(2+h)^2-h+1$

$f(2) =4\cdot 2^2-2+3=4\cdot 4-2+3 =17$

Dan kami mengganti nilai yang ditemukan dalam batasnya:

$\text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}=\\[4ex]=\lim\limits_{h \to 0} \cfrac{4(2+h)^2-h+1-17}{h}=\\[4ex]= \lim\limits_{h \to 0} \cfrac{4(2+h)^2-h-16}{h}$

Kami menghitung persamaan penting:

$\lim\limits_{h \to 0} \cfrac{4(2^2+h^2+2\cdot 2 \cdot h)-h-16}{h}=\lim\limits_{h \to 0} \cfrac{4(4+h^2+4h)-h-16}{h}$

Kami beroperasi pada pembilang:

$\lim\limits_{h \to 0} \cfrac{16+4h^2+16h-h-16}{h}=\lim\limits_{h \to 0} \cfrac{4h^2+15h}{h}$

Sekarang mari kita coba menyelesaikan limitnya:

$\lim\limits_{h \to 0} \cfrac{4h^2+15h}{h}=\cfrac{4\cdot0^2+15\cdot 0}{0} = \cfrac{0}{0}$

Namun kita memperoleh ketidakpastian nol dibagi nol, jadi kita memfaktorkan polinomialnya dan menyederhanakannya:

$\lim\limits_{h \to 0} \cfrac{4h^2+15h}{h}=\lim\limits_{h \to 0} \cfrac{h(4h+15)}{h}=\lim\limits_{h \to 0} \cfrac{\cancel{h}(4h+15)}{\cancel{h}}= \lim\limits_{h \to 0}(4h+15)$

Dan akhirnya, kami menyelesaikan batasannya:

$\lim\limits_{h \to 0}(4h+15)=4\cdot 0+15 =\bm{15}$

Belum:

$\mathbf{TVI} \bm{(2) = 15}$

Berapa tingkat perubahannya?

Tingkat perubahan rata-rata

Contoh penghitungan rata-rata laju perubahan suatu fungsi

Interpretasi geometris dari tingkat perubahan rata-rata

Tingkat perubahan seketika

Contoh penghitungan laju perubahan sesaat suatu fungsi

Interpretasi geometris dari laju perubahan sesaat

Latihan terpecahkan tentang tingkat perubahan

Latihan 1

Latihan 2

Latihan 3

Latihan 4

Latihan 5

Latihan 6

Latihan 7

Tinggalkan Komentar Batalkan Balasan