Vektor koplanar (atau koplanar)

Di halaman ini Anda akan mempelajari apa itu vektor koplanar dan cara mengetahui apakah 2, 3, 4 atau lebih vektor adalah koplanar. Selain itu, Anda akan dapat melihat contoh dan latihan yang diselesaikan selangkah demi selangkah dari vektor koplanar.

Apa yang dimaksud dengan vektor koplanar?

Dalam geometri analitik, pengertian vektor koplanar (atau coplanar) adalah sebagai berikut:

Vektor koplanar adalah vektor yang berada pada bidang yang sama.

Oleh karena itu, dua vektor selalu koplanar karena sebuah bidang dapat dibentuk dengan sedikitnya 2 vektor. Sebaliknya, jika terdapat 3, 4 atau lebih vektor, ada kemungkinan salah satu vektor tersebut tidak berada pada bidang yang sama sehingga tidak sebidang.

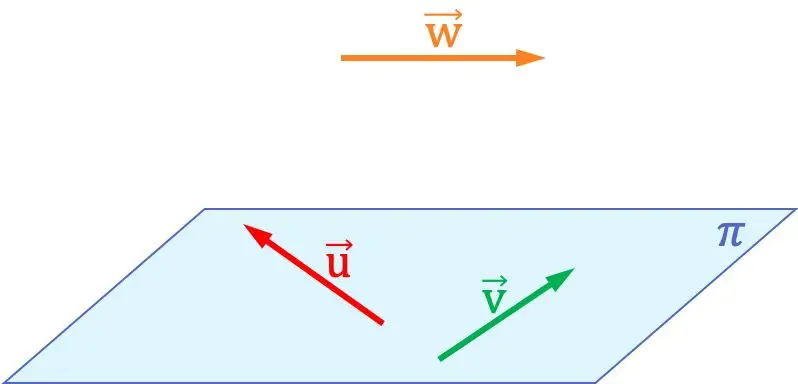
Misalnya, pada grafik di atas Anda dapat melihat vektor-vektornya

$\vv{\text{u}}$

Dan

$\vv{\text{v}}$

mereka sebidang satu sama lain, karena mereka berada dalam bidang yang sama. Sebaliknya, kedua vektor ini tidak sebidang dengan vektor tersebut

$\vv{\text{w}}$

, karena tidak ada bidang yang dapat terbentuk pada ruang yang memuat ketiga vektor tersebut.

Dari sifat ini kita dapat menyimpulkan bahwa jika 3 vektor atau lebih bersifat koplanar, maka titik-titik yang membatasi vektor-vektor tersebut (awal dan akhir vektor) juga merupakan titik-titik koplanar.

Kapankah vektor bersifat koplanar?

Seperti yang kita lihat dalam definisi vektor koplanar (atau koplanar), dua vektor selalu koplanar, tetapi lebih dari dua vektor tidak harus memperhatikan hubungan koplanaritas.

Jadi, ada beberapa metode untuk menentukan apakah tiga vektor atau lebih bersifat koplanar:

Jika hasil kali campuran tiga vektor (atau hasil kali tiga titik) sama dengan nol, berarti ketiga vektor tersebut sebidang. Jika Anda kurang paham tentang cara menghitung operasi ini, saya sarankan Anda untuk melihat hasil kali campuran tiga vektor , di sini Anda akan menemukan penjelasan serta contoh dan latihan yang diselesaikan.

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] =0$

Jika suatu himpunan vektor dapat dinyatakan sebagai kombinasi linier dari dua vektor, maka vektor-vektor tersebut koplanar, artinya 3 atau lebih vektor adalah koplanar jika dan hanya jika vektor-vektor tersebut bergantung linier. Untuk menunjukkan bahwa tiga vektor atau lebih merupakan kombinasi linier dari dua vektor, pangkat matriks yang dibentuk oleh semua vektor tersebut cukup sama dengan 2.

$rg(A) = 2$

Penting bagi Anda untuk memiliki pemahaman yang baik tentang konsep ketergantungan dan kemandirian linier , yaitu kapan dua vektor bergantung linier atau bebas linier, dan apa artinya. Jika Anda belum sepenuhnya paham, di tautan tersebut Anda akan menemukan penjelasan yang sangat mendetail, di mana, selain itu, Anda dapat melihat contoh dan latihan yang diselesaikan langkah demi langkah.

Jika vektor-vektor yang dimaksud adalah vektor-vektor sejajar , berarti vektor-vektor tersebut juga koplanar, yaitu semua vektor-vektor sejajar terdapat pada bidang yang sama.

$\vv{\text{u}} \parallel \vv{\text{v}} \parallel \vv{\text{w}}$

Memecahkan masalah vektor koplanar

Latihan 1

Tentukan apakah ketiga vektor berikut koplanar:

$\vv{\text{u}} = (3,1,2)$

$\vv{\text{v}} = (2,3,-1)$

$\vv{\text{w}} = (-1,-5,4)$

lihat solusi

Untuk memeriksa apakah ini adalah 3 vektor koplanar, kita harus menghitung hasil kali campuran antara ketiga vektor tersebut:

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 3 & 1 & 2 \\[1.1ex] 2 & 3 & -1 \\[1.1ex] -1 & -5 & 4 \end{vmatrix} \\[2ex] &= 36+1-20+6-15-8 \\[2ex] & = \bm{0} \end{aligned}$

Hasil kali campuran ketiga vektor tersebut adalah nol, sehingga ketiga vektor tersebut koplanar .

Latihan 2

Tentukan apakah ketiga vektor berikut koplanar:

$\vv{\text{u}} = (4,-2,6)$

$\vv{\text{v}} = (-2,1,-3)$

$\vv{\text{w}} = (6,-3,9)$

lihat solusi

Salah satu cara untuk memeriksa apakah kita berhadapan dengan 3 vektor koplanar adalah dengan menyelesaikan hasil kali campuran antara ketiga vektor tersebut. Namun jika kita perhatikan lebih dekat komponen-komponen vektornya, kita dapat melihat bahwa vektor-vektor tersebut proporsional. Oleh karena itu, ketiga vektor tersebut sejajar satu sama lain.

$\vv{\text{u}} \parallel \vv{\text{v}} \parallel \vv{\text{w}}$

Dan karena semua vektornya sejajar, maka keduanya merupakan 3 vektor koplanar .

Latihan 3

Tentukan apakah keempat vektor berikut koplanar:

$\vv{\text{a}} = (2,1,1)$

$\vv{\text{b}} = (1,-1,2)$

$\vv{\text{c}} = (-1,0,-1)$

$\vv{\text{d}} = (3,1,2)$

lihat solusi

Untuk mengetahui apakah keempat vektor tersebut koplanar, kita harus menghitung pangkat matriks yang terdiri dari semua vektor:

$\displaystyle A= \begin{pmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{pmatrix}$

Dalam hal ini, kami menghitung ruang lingkup matriks tersebut berdasarkan determinan:

$rg(A) = \ ?$

$\displaystyle \begin{vmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex] -1&0&-1 \end{vmatrix}=0 \quad \begin{vmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex]3&1&2\end{vmatrix} =0$

$\displaystyle \begin{vmatrix} 2&1&1 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{vmatrix}=0 \quad \begin{vmatrix} 1&-1&2 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{vmatrix}=0$

$\displaystyle \begin{vmatrix} 2&1 \\[1.1ex] 1&-1\end{vmatrix}= -3\neq 0$

$rg(A) = 2$

Pangkat matriks yang dibentuk oleh semua vektor ekuivalen dengan 2, sehingga keempat vektor tersebut koplanar .

Latihan 4

Hitung nilai parameter

$k$

sehingga 4 poin berikut ini koplanar:

$A(3,1,4)$

$B(2,1,2)$

$C(0,-1,3)$

$D(3,2,k)$

lihat solusi

Agar keempat titik tersebut koplanar, vektor-vektor yang ditentukan oleh titik-titik tersebut harus koplanar. Oleh karena itu kami menghitung vektor-vektor ini:

$\vv{AB} = B- A = (2,1,2)-(3,1,4) = (-1,0,-2)$