Jarak antara dua garis dalam ruang (dalam r3)

Di halaman ini, Anda akan mengetahui cara menghitung jarak antara dua garis dalam ruang (dalam R3), apa pun jenisnya (garis sejajar, garis potong, berimpit, garis potong, tegak lurus, dll.). Selain itu, Anda akan dapat melihat contoh dan latihan yang diselesaikan langkah demi langkah.

Cara menghitung jarak antara dua garis

Jarak antara dua garis adalah jarak minimum antara suatu titik pada satu garis dan titik mana pun pada garis lainnya. Jarak ini sama dengan panjang ruas garis yang berpindah dari satu garis ke garis lainnya dan sekaligus tegak lurus terhadap kedua garis tersebut.

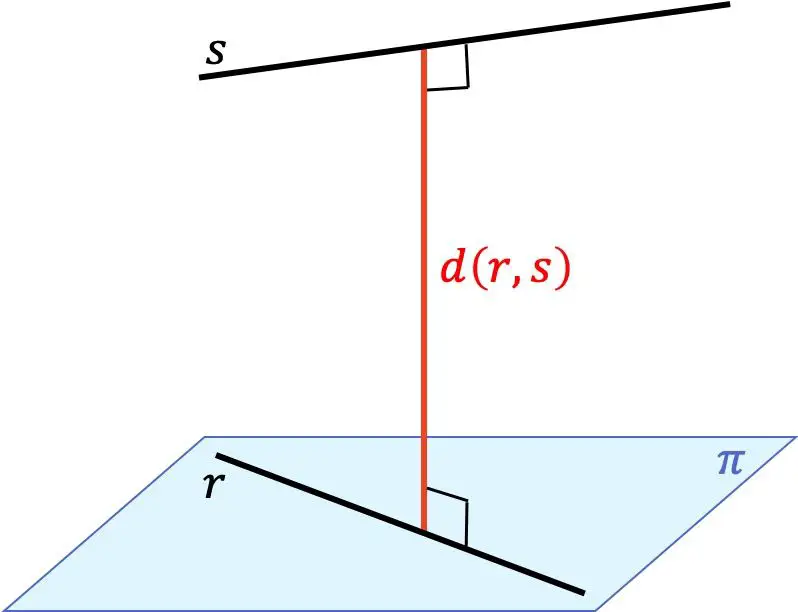
jarak antara dua garis dalam ruang (dalam R3)

Jadi, mencari jarak antara dua garis berbeda dalam ruang tiga dimensi (3D) bergantung pada posisi relatif di antara keduanya:

  • Jika kedua garis tersebut berimpit atau berpotongan , maka jarak kedua garis tersebut adalah nol, karena keduanya berpotongan (setidaknya) di satu titik.
  • Jika kedua garis sejajar , kita perlu mengambil titik mana pun pada salah satu garis dan menghitung jarak antara titik tersebut dan garis lainnya (di bawah ini Anda memiliki contoh cara melakukannya).
  • Jika dua garis berpotongan dalam ruang, kita perlu menerapkan rumus jarak antara dua garis yang berpotongan (lihat penjelasan detailnya di bawah).

Jadi, untuk menghitung jarak antara dua garis, pertama-tama Anda harus mengetahui jenis garisnya dan kemudian, tergantung kasusnya, gunakan satu rumus atau lainnya. Oleh karena itu, penting bagi Anda untuk menguasai cara mencari posisi relatif dua garis dalam ruang sebelum melanjutkan, namun jika Anda tidak ingat cara melakukannya di tautan, Anda akan melihat penjelasan yang sangat lengkap serta contoh dan latihan yang diselesaikan. selangkah demi selangkah.

Cara mencari jarak antara dua garis sejajar dalam ruang

Menghitung jarak antara dua garis sejajar dalam ruang (di R3) dilakukan dengan cara yang sama seperti di bidang (di R2): Anda harus mengambil sebuah titik di salah satu dari dua garis tersebut dan mencari jarak titik tersebut di garis lainnya. garis.

jarak antara dua garis sejajar dalam ruang

Jadi, rumus menghitung jarak suatu titik ke garis 3 dimensi (yang digunakan untuk menentukan jarak antara dua garis sejajar) adalah:

d(s,r)=d(P,r)=\cfrac{\lvert \vv{QP} \times \vv{\text{v}}_r \rvert}{\lvert \vv{\text{v}}_r \rvert}

Emas:

  • \lvert \vv{\text{v}}_r \rvert

    adalah besarnya vektor arah garis

    r.

  • Q

    adalah sebuah titik pada garis

    r,

    P

    suatu titik pada garis tersebut

    s

    Dan

    \vv{QP}

    vektor yang ditentukan oleh dua titik

  • \lvert \vv{QP} \times \vv{\text{v}}_r \rvert

    adalah besarnya perkalian silang antar vektor

    \vv{QP}

    Dan

    \vv{\text{v}}_r

Sebagai contoh, kita akan menyelesaikan soal jarak antara 2 garis sejajar dalam ruang:

  • Berapa jarak antara dua garis sejajar berikut?

r: \ (x,y,z) = (2,1,1) + t(-1,3,2)

s: \ (x,y,z) = (-2,4,1) + t(2,-6,-4)

Kedua garis tersebut dinyatakan dalam bentuk persamaan vektor, sehingga kita dapat dengan mudah mengetahui vektor arah dan titik dari masing-masing garis tersebut:

\displaystyle r : \ \begin{cases}\vv{\text{v}}_r=(-1,3,2) \\[1.7ex] Q(2,1,1) \end{cases} \qquad \qquad s: \ \begin{cases}\vv{\text{v}}_s=(2,-6,-4) \\[1.7ex] P(-2,4,1) \end{cases}

Jika Anda ragu tentang cara menentukan vektor arah dan titik suatu garis, kami sarankan Anda menyimak penjelasan persamaan garis . Di sana kami menjelaskannya untuk semua persamaan garis, karena mencari vektor arah dan titik yang termasuk dalam suatu garis bergantung pada jenis persamaan yang menyatakan garis tersebut.

Sekarang, untuk mencari jarak antara dua garis sejajar, kita perlu menerapkan rumus jarak titik ke garis:

d(s,r)=d(P,r)=\cfrac{\lvert \vv{QP} \times \vv{\text{v}}_r \rvert}{\lvert \vv{\text{v}}_r \rvert}

Jadi di satu sisi kita menghitung modul vektor yang dihasilkan dari perkalian vektor. Jika Anda ragu tentang cara menghitungnya, Anda dapat melihat rumus perkalian vektor , di mana, selain itu, Anda akan dapat melihat contoh dan menyelesaikan latihan operasi antar vektor ini.

\vv{QP} = Q - P = (2,1,1)-(-2,4,1) = (4,-3,0)

\vv{QP} \times \vv{\text{v}}_r =\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 4&-3&0 \\[1.1ex] -1&3&2 \end{vmatrix}=-6\vv{i} -8\vv{j}+9\vv{k}

\left|\vv{QP} \times \vv{\text{v}}_r \right| =\sqrt{(-6)^2+(-8)^2+9^2} = \sqrt{36+64+81} = \sqrt{181}

Dan sebaliknya, kita mencari besar vektor garis tersebut

r:

\lvert \vv{\text{v}}_r \rvert = \sqrt{(-1)^2+3^2+2^2} = \sqrt{1+9+4} = \sqrt{14}

Terakhir, kita substitusikan nilai setiap suku ke dalam rumus dan hitung jarak antar garis:

d(s,r)=d(P,r)=\cfrac{\lvert \vv{QP} \times \vv{\text{v}}_r \rvert}{\lvert \vv{\text{v}}_r \rvert}=\cfrac{\sqrt{181}}{\sqrt{14}} = \bm{3,60}

Jadi, jarak kedua garis tersebut adalah 3,60 satuan.

Cara menentukan jarak antara dua garis yang berpotongan dalam ruang

Seperti yang sudah kita lihat di awal, cara menentukan jarak antara dua garis yang berpotongan berbeda dengan cara menentukan jarak antara garis sejajar.

jarak antara garis bersilang dalam ruang

Oleh karena itu, ada beberapa cara untuk menentukan jarak antara dua garis yang berpotongan dalam ruang. Pada halaman ini kami hanya akan menjelaskan satu prosedur, yang paling sederhana, karena dua metode lainnya lebih panjang dan rumit, bahkan praktis tidak digunakan.

Misalkan vektor arah dan titik mana pun pada dua garis yang berpotongan adalah:

\displaystyle r: \ \begin{cases} \vv{\text{u}} \\[2ex] A\end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}} \\[2ex] B\end{cases}

Rumus jarak antara dua garis yang berpotongan adalah:

d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert}

Emas

\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|

adalah nilai mutlak hasil kali campuran vektor-vektor tersebut

\vv{\text{u}}, \vv{\text{v}}

dan vektor yang ditentukan oleh titik-titik

A

Dan

B

. Dan di sisi lain,

\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert

adalah amplitudo perkalian silang antara vektor arah dari dua garis yang bersilangan.

Agar Anda dapat mengetahui cara menentukan jarak antara dua garis yang bersilangan, kita akan menyelesaikan soal sebagai contoh:

  • Berapa jarak antara dua garis berpotongan berikutnya?

r: \ \cfrac{x-1}{2} = \cfrac{y-2}{4} = \cfrac{z+2}{-1}

s: \ \cfrac{x-3}{1} = \cfrac{y+1}{3} = \cfrac{z-1}{-2}

Pertama, kita perlu mengidentifikasi vektor arah dan titik pada setiap garis. Kedua garis tersebut dinyatakan dalam bentuk persamaan kontinu, oleh karena itu:

\displaystyle r: \ \begin{cases} \vv{\text{u}} =(2,4,-1) \\[2ex] A(1,2,-2) \end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}}=(1,3,-2) \\[2ex] B(3,-1,1)\end{cases}

Dan sekarang kita terapkan rumus jarak antara dua garis yang berpotongan:

d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert}

Di satu sisi kita menyelesaikan produk campuran (atau produk skalar rangkap tiga):

\vv{AB} = B - A = (3,-1,1) - (1,2,-2) = (2,-3,3)

\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right| =\left| \begin{vmatrix} 2&4&-1 \\[1.1ex] 1&3&-2 \\[1.1ex] 2&-3&3 \end{vmatrix}\right| = \left| -13 \right| =13

Dan, di sisi lain, kita menemukan modul perkalian silang (atau perkalian silang):

\vv{\text{u}} \times \vv{\text{v}} =\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 2&4&-1 \\[1.1ex] 1&3&-2 \end{vmatrix}=-5\vv{i} +3\vv{j}+2\vv{k}

\left| \vv{\text{u}} \times \vv{\text{v}} \right| =\sqrt{5^2+3^2+2^2} = \sqrt{25+9+4} = \sqrt{38}

Terakhir, kita substitusikan nilai setiap suku ke dalam rumus jarak antara dua garis yang bersilangan:

d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert} = \cfrac{13}{\sqrt{38}}= \bm{2,11}

Tinggalkan Komentar

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *

Scroll to Top