Di halaman ini kamu akan mengetahui apa itu bidang tegak lurus, cara menentukan dua bidang tegak lurus, cara menghitung bidang tegak lurus, contoh dan latihan soal bidang tegak lurus,…
Berapakah dua bidang yang tegak lurus?
Dalam geometri analitik, dua bidang tegak lurus jika berpotongan tegak lurus (90º).
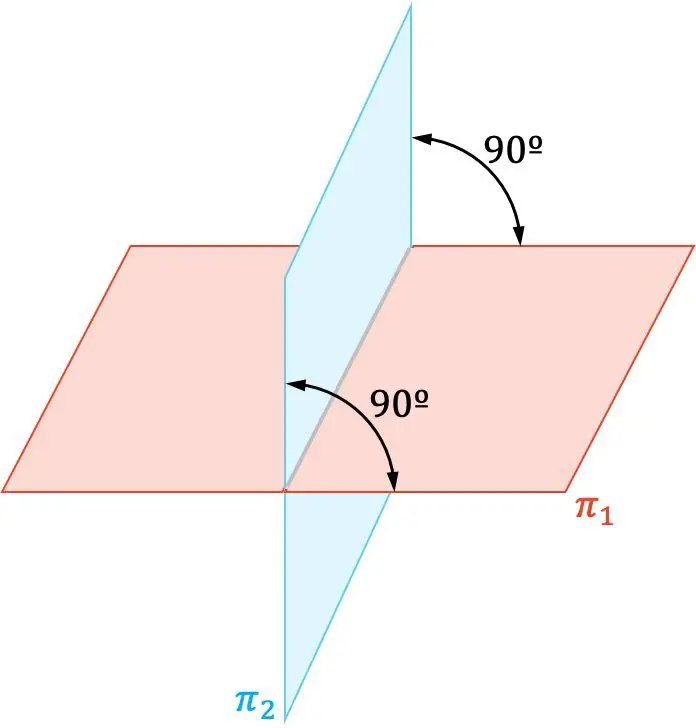
Selain itu, vektor normal dua bidang yang tegak lurus juga ortogonal satu sama lain.
Jelasnya, jarak antara dua bidang yang tegak lurus selalu nol, karena keduanya berpotongan dalam satu garis. Meski terkesan sangat sederhana, namun konsep jarak antara dua bidang sangatlah penting, oleh karena itu kami sarankan untuk mengunjungi tautan tersebut jika Anda memiliki pertanyaan mengenai hal tersebut.
Sebaliknya, dua bidang yang posisinya tegak lurus bukan satu-satunya kemungkinan posisi relatif antar bidang, karena dua bidang dalam ruang (dalam R3) juga dapat berpotongan, sejajar, atau berhimpitan.
Bagaimana cara mengetahui apakah suatu bidang tegak lurus terhadap bidang lainnya?
Setelah kita melihat pengertian bidang tegak lurus, mari kita lihat cara mengetahui dua bidang tegak lurus atau tidak:
Dua bidang tegak lurus jika vektor normalnya tegak lurus. Oleh karena itu, untuk menentukan apakah dua bidang tegak lurus satu sama lain, kita harus menghitung sudut yang dibentuk oleh vektor-vektor normalnya, dan jika membentuk sudut 90º, berarti bidang-bidang tersebut tegak lurus.
Jadi untuk mencari tegak lurus dua bidang, Anda perlu mengetahui cara menghitung sudut antara dua vektor . Jika Anda tidak ingat cara melakukannya, Anda dapat melihat tautannya, di mana Anda akan menemukan penjelasan kami serta rumus yang diperlukan untuk menentukan sudut antara dua vektor. Selain itu, Anda akan dapat melihat contoh dan latihan dengan latihan yang diselesaikan.
Singkatnya, dua vektor tegak lurus jika hasil kali titiknya nol. Oleh karena itu, dua bidang akan tegak lurus jika hasil kali titik dari vektor-vektor normal yang berhubungan adalah 0.
Contoh dua bidang yang tegak lurus
Misalnya, mari kita periksa apakah dua bidang berikut tegak lurus:
![]()
![]()
Koordinat X, Y, Z dari vektor normal bidang bertepatan dengan koefisien A, B, C dari persamaan umum (atau implisit). Oleh karena itu, vektor normal pada setiap bidang adalah:
![]()
![]()
Dan sekarang kita periksa apakah ini adalah dua bidang tegak lurus dengan menghitung perkalian titik antara vektor normalnya:
![Rendered by QuickLaTeX.com \begin{aligned} \vv{n}_1 \cdot \vv{n}_2 & = (3,-4,2)\cdot (2,5,7) \\[2ex] & = 3 \cdot 2 +(-4) \cdot 5 +2 \cdot 7 \\[2ex] &=6-20+14 \\[2ex] &\bm{= 0}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-94cfcef6a93720224eff0bd4891839ed_l3.png)
Hasil kali titik antara dua vektor normal adalah 0, jadi kedua bidang saling tegak lurus .
Menghitung bidang yang tegak lurus terhadap garis di suatu titik
Masalah bidang dan garis yang umum adalah mencari persamaan bidang yang tegak lurus garis pada suatu titik tertentu. Jadi, selanjutnya kita akan melihat bagaimana penyelesaiannya melalui sebuah contoh:
- Temukan persamaan bidang yang tegak lurus garis.

Tentang
dikatakan secara lugas dan tepat:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=3-2t \\[1.7ex] y=-1+4t \\[1.7ex] z=1+t \end{cases} \qquad \qquad P(1,3,-2)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1ac7260ee9792daec4f32e1f200df01b_l3.png)
Pertama, kita perlu mencari vektor normal bidang yang bersangkutan. dan seperti garis lurus
![]()
tegak lurus terhadap bidang, vektor normalnya akan berimpit dengan vektor arah garis.
Dalam hal ini, garis
![]()
berbentuk persamaan parametrik, sehingga komponen vektor arahnya adalah suku-suku di depan parameternya
![]()
![]()
Jadi, vektor tegak lurus bidang akan sama dengan vektor arah garis:
![]()
Oleh karena itu, persamaan implisit (atau umum) dari rencana tersebut adalah sebagai berikut:
![]()
Oleh karena itu, cukup menentukan nilai koefisien D. Untuk melakukannya, kita substitusikan koordinat titik yang pernyataannya menyatakan bahwa titik tersebut termasuk bidang ke dalam persamaannya:
![]()
![]()
![]()
![]()
![]()
Singkatnya, persamaan bidang kartesius adalah:
![]()
Sebaliknya, jika Anda ingin lebih banyak berlatih latihan tentang tegak lurus antar objek geometris, Anda dapat mengunjungi halaman kami tentang garis tegak lurus. Anda akan menemukan semua yang perlu Anda ketahui tentang garis tegak lurus : ketika dua garis tegak lurus, cara menghitung satu garis tegak lurus dengan garis lainnya, contoh, latihan penyelesaian, dan banyak lagi.
Sifat-sifat bidang tegak lurus
Semua bidang tegak lurus mempunyai ciri-ciri sebagai berikut:
- Hubungan simetris : Jika suatu bidang tegak lurus terhadap bidang lain, maka bidang tersebut juga tegak lurus terhadap bidang pertama. Sifat ini juga dimiliki oleh bidang sejajar.
![]()
- Sifat non-refleksif : Jelas, tidak ada bidang yang tegak lurus terhadap dirinya sendiri.
![]()
- Dalil: Dalam ruang tiga dimensi (3D), setiap pasangan bidang yang tegak lurus terhadap bidang ketiga harus sejajar. Dengan kata lain, jika sebuah bidang tegak lurus terhadap bidang lain dan bidang tersebut juga tegak lurus terhadap bidang ketiga, maka bidang pertama dan terakhir sejajar satu sama lain.