Persamaan bidang implisit, umum atau Cartesian

Penjelasan tentang cara menghitung persamaan bidang implisit (rumus), disebut juga persamaan umum atau persamaan kartesius. Selain itu, Anda akan menemukan cara mencari persamaan bidang dari vektor normalnya. Dan terlebih lagi, Anda akan dapat melihat contoh dan latihan yang diselesaikan langkah demi langkah.

Apa persamaan implisit atau umum dari rencana tersebut?

Dalam geometri analitik, persamaan implisit suatu bidang , disebut juga persamaan bidang umum atau Cartesian , adalah persamaan yang memungkinkan bidang apa pun dinyatakan secara matematis. Untuk mencari persamaan implisit atau persamaan umum suatu bidang, kita memerlukan sebuah titik dan dua vektor bebas linier yang dimiliki bidang tersebut.

Rumus persamaan denah implisit atau umum

Perhatikan sebuah titik dan dua vektor arah pada sebuah bidang:

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

Persamaan implisit, umum, atau Cartesian suatu bidang diperoleh dengan menyelesaikan determinan berikut dan menetapkan hasilnya sama dengan 0:

$\displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0$

Dengan demikian, persamaan implisit atau umum dari rencana yang dihasilkan adalah sebagai berikut:

$Ax+By+Cz+D=0$

Penting agar kedua vektor dalam rumus tersebut bebas linier satu sama lain, artinya keduanya harus memiliki arah yang berbeda. Dan untuk memenuhi syarat ini cukuplah kedua vektor tersebut tidak sejajar.

persamaan implisit atau umum atau Cartesian dari pan xy di r3

Meski tidak perlu mengetahui alasan rumus ini, Anda bisa melihat demonstrasinya di bawah ini.

Dimulai dari persamaan parametrik suatu denah, kita akan beralih ke persamaan implisit (atau umum) dari denah tersebut:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Pertama, kita meneruskan suku independen dari setiap persamaan parametrik ke sisi persamaan lainnya:

$\displaystyle \begin{cases}x-P_x= \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y-P_y = \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z-P_z = \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Atau setara:

$\displaystyle \begin{cases} \lambda \text{u}_x + \mu \text{v}_x =x-P_x\\[1.7ex] \lambda \text{u}_y + \mu \text{v}_y=y-P_y \\[1.7ex] \lambda\text{u}_z + \mu \text{v}_z =z-P_z\end{cases}$

Agar sistem persamaan di atas mempunyai penyelesaian yang layak, pangkat matriks berikut harus sama dengan 2 (teorema Rouche-Frobenius):

$\displaystyle\begin{pmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z\end{pmatrix}$

Jadi jika range matriks sebelumnya harus dua, maka determinan 3×3 harus sama dengan nol:

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

Dan dengan menyelesaikan determinan ini, kita memperoleh persamaan umum, implisit, atau Cartesian sebuah bidang:

$Ax+By+Cz+D=0$

Jadi, kita baru saja melihat persamaan implisit (atau umum) dan persamaan parametrik bidang, namun ada lebih banyak cara untuk menyatakan bidang secara analitis, seperti persamaan vektor dan persamaan kanonik. Rumus dan penjelasan seluruh persamaan pada denah dapat Anda lihat pada tautan ini.

Contoh cara mencari persamaan bidang secara implisit atau umum

Mari kita lihat cara menentukan persamaan implisit (atau umum atau Cartesian) sebuah bidang melalui sebuah contoh:

Temukan persamaan implisit atau umum dari bidang yang melalui titik tersebut
$P(3,1,-1)$

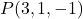
dan berisi vektor

$\vv{\text{u}}=(2,0,3)$

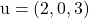
Dan

$\vv{\text{v}}=(4,-1,2).$

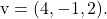
Untuk menghitung persamaan umum atau implisit bidang, perlu diselesaikan determinan yang dibentuk oleh dua vektor, variabel dan koordinat titik berikut:

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

Jadi, kita substitusikan vektor dan titik ke dalam rumus:

$\displaystyle\begin{vmatrix}2 & 4 & x-3 \\[1.1ex]0 & -1 & y-1 \\[1.1ex]3& 2 & z-(-1) \end{vmatrix} =0$

$\displaystyle\begin{vmatrix}2 & 4 & x-3 \\[1.1ex]0 & -1 & y-1 \\[1.1ex]3& 2 & z+1 \end{vmatrix} =0$

Dan sekarang kita selesaikan determinan orde 3, misalnya dengan aturan Sarrus atau dengan kofaktor (atau deputi):

$-2(z+1)+12(y-1)+3(x-3)-4(y-1) = 0$

Sekarang kami mengoperasikan dan mengelompokkan istilah-istilahnya:

$3(x-3)+8(y-1) -2(z+1) = 0$

$3x-9+8y-8 -2z-2 = 0$

$3x+8y-2z-19 = 0$

Oleh karena itu, persamaan implisit atau umum dari rencana tersebut adalah:

$\bm{3x+8y-2z-19 = 0}$

Hitung persamaan implisit atau umum suatu bidang dari vektor normalnya

Masalah yang sangat umum dalam persamaan bidang adalah mencari persamaan bidang tertentu jika diberi sebuah titik dan vektor normalnya (atau tegak lurus). Jadi, mari kita lihat cara kerjanya.

Namun perlu diketahui terlebih dahulu bahwa komponen X, Y, Z dari vektor tegak lurus bidang tersebut masing-masing berimpit dengan koefisien A, B, C dari persamaan implisit (atau umum) bidang tersebut.

$\displaystyle \color{orange} \boxed{ \color{black} \quad \pi : \ Ax+By+C+D = 0 \quad \iff \quad \vv{n} = (A,B,C) \quad \vphantom{\Bigl(}}$

Emas

$\vv{n}$

adalah vektor ortogonal terhadap bidang

$\pi.$

Setelah kita mengetahui hubungan sebelumnya, mari kita lihat contoh penyelesaian soal persamaan bidang jenis ini:

Tentukan persamaan implisit atau umum bidang yang melalui titik tersebut
$P(1,0,-2)$

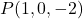
dan salah satu vektor normalnya adalah

$\vv{n}=(3,-1,2) .$

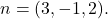
Rumus persamaan bidang implisit, umum, atau kartesius adalah:

$Ax+By+Cz+D=0$

Jadi, dari vektor normal kita dapat mencari koefisien A, B dan C karena ekuivalen dengan komponen-komponen vektor normalnya:

$\vv{n}=(3,-1,2) \ \longrightarrow \ 3x-1y+2z+D=0$

Sedangkan kita hanya perlu mencari parameter D. Caranya, kita substitusikan koordinat titik milik bidang tersebut ke dalam persamaan:

$P(1,0,-2)$

$3\cdot 1-0+2\cdot (-2)+D=0$

$3-4+D=0$

$-1+D=0$

$D=1$

Jadi persamaan implisit atau umum dari rencana tersebut adalah:

$\bm{3x-y+2z+1 = 0}$

Memecahkan masalah persamaan bidang implisit atau umum

Latihan 1

Temukan persamaan implisit atau umum dari bidang yang melalui titik tersebut

$P(-2,1,3)$

dan berisi vektor

$\vv{\text{u}}=(4,1,3)$

Dan

$\vv{\text{v}}=(5,3,-1).$

lihat solusi

Untuk menghitung persamaan umum atau implisit bidang, perlu diselesaikan determinan yang dibentuk oleh dua vektor, ketiga variabel, dan koordinat titik berikut:

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

Jadi, kita substitusikan vektor dan titik ke dalam rumus:

$\displaystyle\begin{vmatrix}4 & 5 & x+2 \\[1.1ex]1 & 3 & y-1 \\[1.1ex]3& 1 & z+1 \end{vmatrix} =0$

Dan sekarang kita selesaikan determinan matriks 3×3 dengan metode pilihan Anda:

$12(z+1)+15(y-1)+1(x+2)-9(x+2)-4(y-1)-5(z+1) = 0$

Terakhir, kami melakukan operasi dan mengelompokkan istilah serupa:

$-8(x+2)+11(y-1)+7(z+1) = 0$

$-8x-16+11y-11+7z+7=0$

$-8x+11y+7z-20= 0$

Jadi persamaan implisit atau umum dari rencana tersebut adalah:

$\bm{-8x+11y+7z-20 = 0}$

Latihan 2

Tentukan apakah intinya

$P(-1,5,-3)$

milik rencana berikut:

$\pi : \ 2x+y+6z-5=0$

lihat solusi

Agar suatu titik berada pada bidang, persamaannya harus diverifikasi. Oleh karena itu, kita perlu mensubstitusikan koordinat Cartesius titik tersebut ke dalam persamaan bidang dan memeriksa apakah persamaan tersebut terpenuhi:

$2x+y+6z-5=0$

$P(-1,5,-3)$

$2\cdot (-1)+5+6\cdot (-3)-5=0$

$-2+5-18-5=0$

$-20\neq 0$

Intinya tidak memperhatikan persamaan bidang tersebut, sehingga bukan bagian dari bidang tersebut.

Latihan 3

Temukan persamaan implisit (atau umum) dari denah yang memuat tiga poin berikut:

$A(5,-1,-2) \qquad B(2,1,3) \qquad C(4,1,-2)$

lihat solusi

Untuk mencari persamaan implisit bidang tersebut, kita perlu mencari dua vektor bebas linier yang terikat pada bidang tersebut. Dan untuk ini, kita dapat menghitung dua vektor yang ditentukan oleh 3 titik:

$\vv{AB} = B - A = (2,1,3) - (5,-1,-2) = (-3,2,5)$

$\vv{AC} = C - A = (4,1,-2) - (5,-1,-2) = (-1,2,0)$

Koordinat kedua vektor yang ditemukan tidak proporsional, sehingga keduanya bebas linier satu sama lain.

Sekarang kita sudah mengetahui dua vektor arah dan satu titik pada bidang, sehingga kita sudah dapat menerapkan rumus persamaan umum bidang:

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

Kami mengganti vektor dan salah satu dari tiga titik ke dalam rumus:

$\displaystyle\begin{vmatrix}-3 & -1 & x-5 \\[1.1ex]2 & 2 & y+1 \\[1.1ex]5& 0 & z+2 \end{vmatrix} =0$