Di halaman ini Anda akan menemukan definisi penampang kerucut, mengapa begitu penting dan berbagai jenis penampang kerucut yang ada (lingkaran, elips, hiperbola, dan parabola). Selain itu, Anda akan dapat melihat perbedaan antara persamaannya.
Apa itu bagian berbentuk kerucut?
Dalam geometri analitik, penampang kerucut (atau sederhananya kerucut) adalah semua kurva yang dihasilkan dari perpotongan berbeda antara kerucut dan bidang, ketika bidang tersebut tidak melalui titik puncak kerucut. Ada empat jenis bagian kerucut: lingkaran, elips, parabola, dan hiperbola.
Di bawah ini adalah 4 kemungkinan bagian yang dapat diperoleh dari kerucut apa pun:
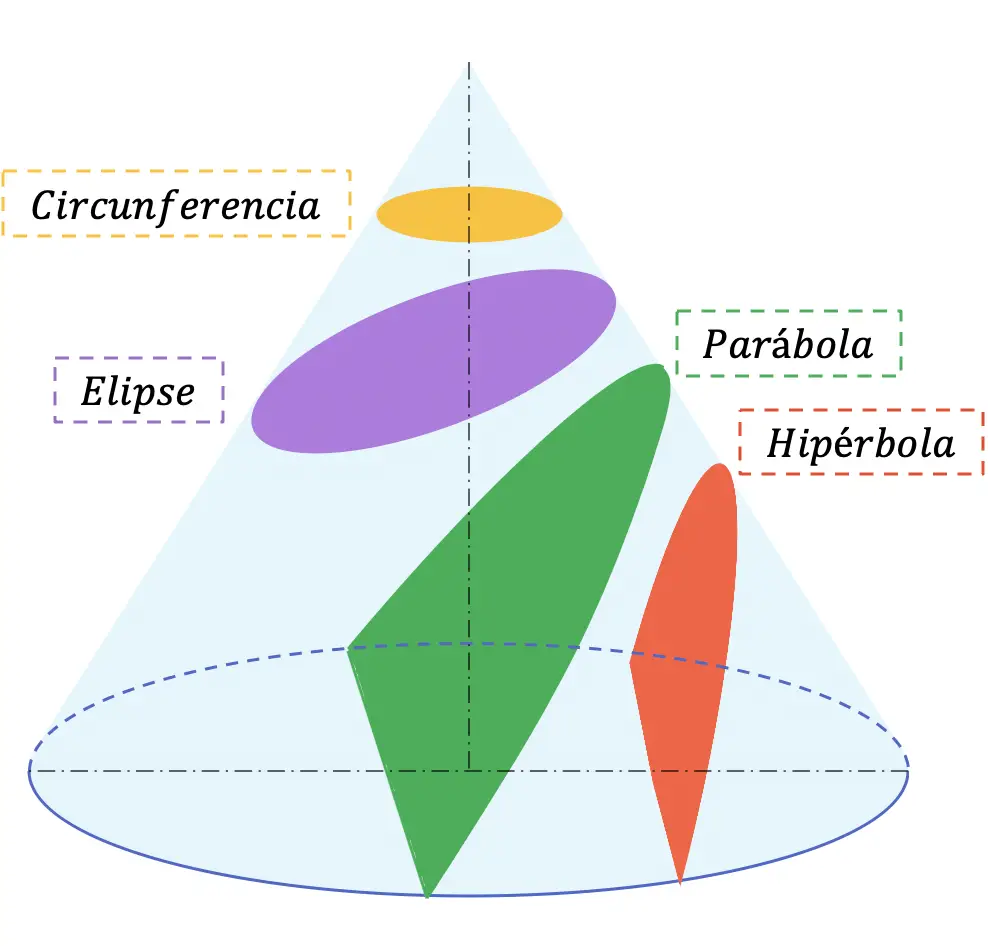
Bagian kerucut umumnya dipelajari di sekolah menengah (Bachillerato), dalam mata pelajaran matematika dan gambar teknik.
Jenis bagian berbentuk kerucut
Setelah kita melihat konsep penampang kerucut, mari kita lihat apa saja empat jenis penampang kerucut yang ada: lingkaran, elips, parabola, dan hiperbola.
lingkar
Keliling adalah bagian kerucut yang dapat dicari dengan memotong kerucut yang bidangnya tegak lurus terhadap sumbu revolusinya (sejajar dengan alas).

Selain itu, keliling adalah tempat kedudukan titik-titik pada bidang yang berjarak sama terhadap suatu titik tetap yang disebut pusat.
Elips
Elips merupakan garis datar, tertutup, melengkung mirip sekali dengan keliling, namun bentuknya lebih lonjong. Secara khusus, hal ini dihasilkan dari pemotongan permukaan kerucut dengan bidang miring yang sudut relatif terhadap sumbu revolusi lebih besar daripada sudut generator.
Selain itu, semua titik pada elips memenuhi syarat: elips adalah tempat kedudukan semua titik pada bidang yang jumlah jarak ke dua titik tetap lainnya (disebut fokus F dan F’) adalah konstan.

Perumpamaan
Dalam matematika, parabola adalah tempat kedudukan titik-titik pada bidang yang berjarak sama terhadap suatu titik tetap (disebut fokus) dan garis tetap (disebut direktriks).

Secara geometris, parabola merupakan hasil potongan kerucut oleh suatu bidang yang sudut kemiringannya relatif terhadap sumbu revolusi setara dengan sudut generatrix kerucut. Oleh karena itu, bidang yang memuat parabola sejajar dengan generator kerucut.
Karakteristik yang sangat penting dari bagian kerucut ini adalah persamaan parabola , karena bergantung pada keadaannya, persamaan ini memungkinkan kita untuk mengidentifikasi jenis parabolanya. Di tautan ini Anda akan menemukan semua persamaan parabola, apa saja unsur-unsur parabola, sifat-sifatnya, contoh, latihan yang diselesaikan,… di antara ciri-ciri parabola lainnya.
Hiperbola
Sebagai bagian berbentuk kerucut, hiperbola diperoleh jika sebuah kerucut dipotong oleh bidang yang sudutnya lebih kecil dari sudut yang dibentuk oleh generator kerucut terhadap sumbu revolusinya.
Secara matematis, hiperbola dapat didefinisikan sebagai tempat kedudukan titik-titik pada bidang yang memenuhi sifat-sifat berikut: nilai absolut selisih jarak antara titik mana pun pada hiperbola dan dua titik tetap (disebut fokus) harus konstan.
Selanjutnya, nilai pengurangan kedua jarak tersebut selalu setara dengan jarak antara dua titik sudut hiperbola.
![]()

Seperti yang saya yakin sudah Anda simpulkan, nilai parameternya
![]()
hiperbola adalah dasar untuk hiperbola. Di tautan berikut Anda dapat melihat penjelasan kami tentang hiperbola, di mana Anda akan mengetahui mengapa koefisien itu begitu penting serta apa saja elemen yang menjadi ciri hiperbola. Selain itu, Anda akan menemukan seperti apa persamaan hiperbola , berbagai jenis hiperbola yang ada, dan bahkan soal langkah demi langkah dan latihan tentang hiperbola.
Persamaan umum bagian kerucut
Setiap bagian berbentuk kerucut dapat dinyatakan secara analitis sebagai persamaan. Faktanya, semua persamaan berbentuk kerucut harus berpangkat kedua:
![]()
Oleh karena itu, setidaknya salah satu koefisien
![]()
salah satu
![]()
rumusnya harus bukan nol.
Jadi, bergantung pada nilai parameternya, persamaan tersebut akan sesuai dengan satu jenis kerucut atau lainnya:
- Keliling : untuk persamaan umum yang menggambarkan keliling, istilahnya

Dan

harus cocok dan

harus nol.
![]()
- Elips : Persamaan akan sesuai dengan ekspresi matematika elips jika kondisi berikut diverifikasi:
![]()
- Parabola : Agar persamaan menjadi parabola, persamaan berikut harus dipenuhi:
![]()
- Hiperbola : Terakhir, persamaan umum hiperbola harus memenuhi pertidaksamaan berikut:
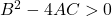 Navigasi pos
Navigasi pos