Di halaman ini Anda akan menemukan arti eksentrisitas elips dan cara menghitungnya (rumus). Selain itu, Anda akan melihat contoh penghitungan eksentrisitas elips.
Berapa eksentrisitas elips?
Eksentrisitas elips adalah parameter yang mengukur seberapa bulat atau rata suatu elips, yaitu eksentrisitas suatu elips menunjukkan seberapa mirip elips tersebut dengan lingkaran.
Di sisi lain, mari kita ingat juga apa yang dimaksud dengan elips: elips adalah tempat kedudukan semua titik pada bidang yang jumlah jarak ke dua titik tetap lainnya (disebut fokus F dan F’) adalah konstan.
Rumus Eksentrisitas Elips
Setelah kita melihat definisi eksentrisitas elips, mari kita lihat cara menghitungnya dari rumusnya:
Rumus eksentrisitas elips adalah sebagai berikut:
![]()
Emas:
-

adalah eksentrisitas elips
-

adalah jarak dari fokus (titik F dan F’) elips ke pusatnya
-

adalah panjang sumbu semi-mayor (atau mayor) elips.
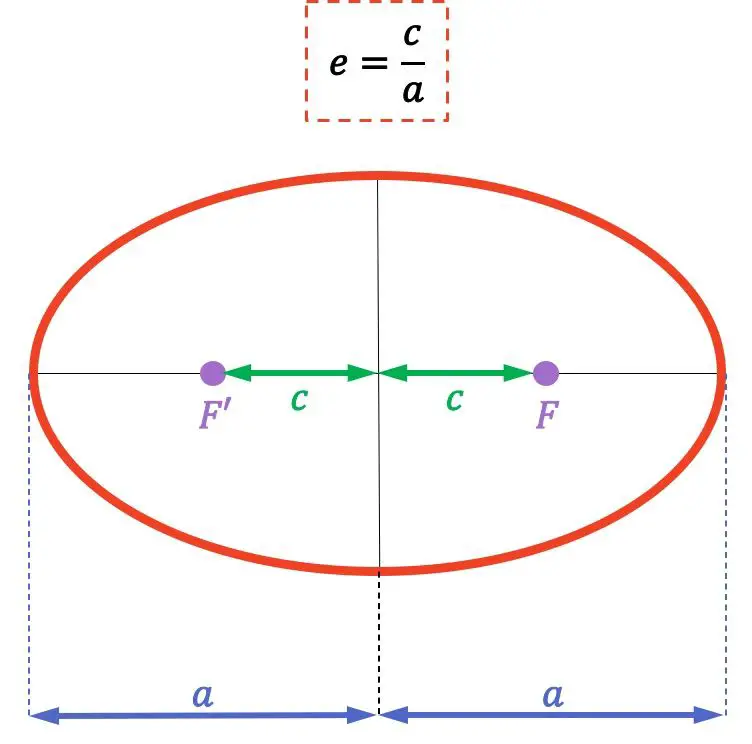
Ingatlah bahwa fokus elips adalah titik-titik tetap yang jumlah jarak ke titik mana pun pada elips adalah konstan. Selain itu, jarak antara dua titik fokus disebut panjang fokus.
Nilai eksentrisitasnya berkisar dari nol yang berarti lingkaran sempurna, hingga satu yang berarti garis mendatar. Tentunya 0 dan 1 tidak dimasukkan karena benda geometris yang dihasilkan bukan lagi elips.

![]()
d(P,F)
![]()
d(P,F’)
![]()
memiliki
![]()
memiliki

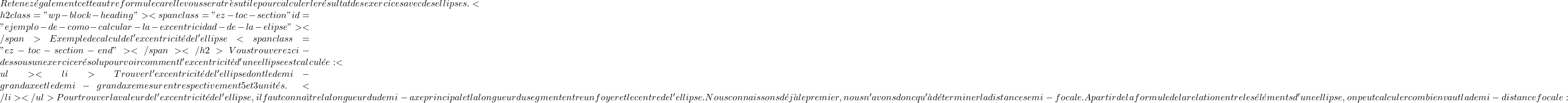
![]()
memiliki
![]()
vs,
![]()
e= \cfrac{c}{a} = \cfrac{4}{5} = \bm{0,8} $