Di sini Anda akan menemukan cara menghitung persamaan (rumus) elips, apakah mempunyai titik asal sebagai pusatnya atau tidak. Anda juga akan mengetahui apa saja elemen elips, cara menghitungnya, dan kegunaannya. Selain itu, Anda akan dapat melihat contoh dan menyelesaikan latihan persamaan elips.
Rumus persamaan elips
Rumus persamaan elips dalam koordinat kartesius adalah:
![]()
Emas:
-

Dan

adalah koordinat pusat elips:
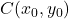
-

adalah jari-jari horizontal elips.
-

adalah jari-jari vertikal elips.
Persamaan elips berpusat pada titik asal
Jenis elips yang paling umum adalah elips yang pusatnya berada di titik asal koordinat, yaitu di titik (0,0). Inilah sebabnya kita akan melihat bagaimana mencari persamaan elips yang berpusat di titik asal.
Berikut rumus persamaan elips:
![]()
Jika elips berpusat pada titik asal koordinat, berarti demikian
![]()
Dan
![]()
sama dengan 0, maka persamaannya adalah:
![]()
Ada ahli matematika yang juga menyebut ungkapan ini sebagai persamaan kanonik atau persamaan elips tereduksi.
elemen elips
Setelah kita melihat seperti apa persamaan elipsnya, kita akan melihat apa saja elemen-elemennya. Tapi pertama-tama, mari kita ingat apa sebenarnya elips:
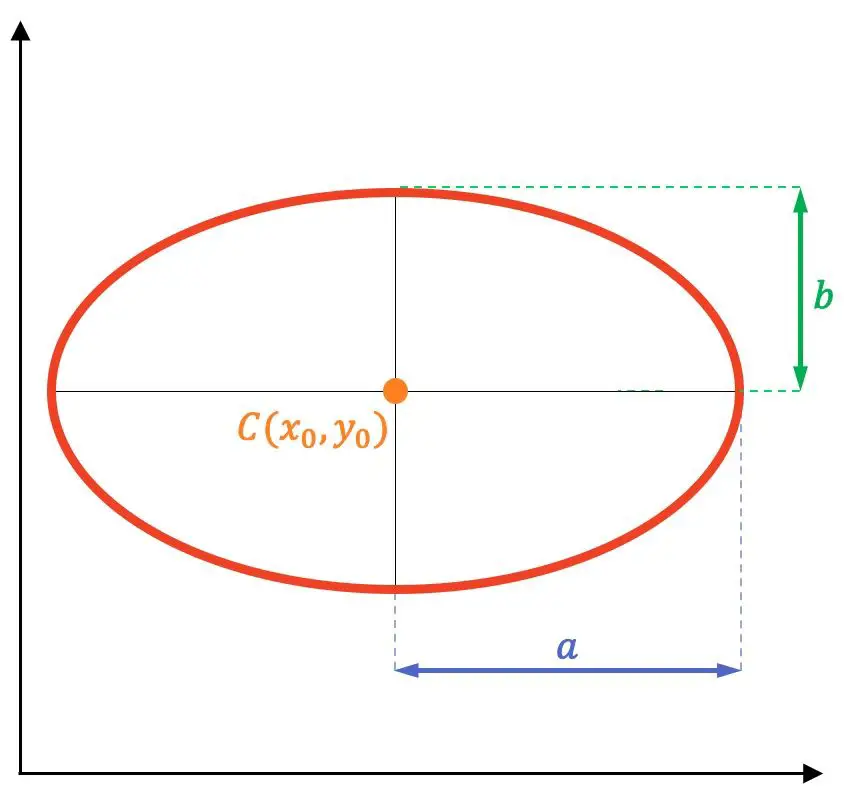
Elips merupakan garis datar, tertutup, melengkung mirip sekali dengan keliling, namun bentuknya lebih lonjong. Secara khusus, elips adalah tempat kedudukan semua titik pada suatu bidang yang jumlah jarak ke dua titik tetap lainnya (disebut fokus F dan F’) adalah konstan.
Jadi, unsur-unsur elips adalah:
- Fokus : ini adalah titik tetap F dan F’ (titik berwarna ungu pada gambar di bawah). Jumlah jarak antara titik mana pun pada elips dan setiap fokus adalah konstan untuk semua titik pada elips.
- Sumbu utama atau fokus : ini adalah sumbu simetri elips tempat titik fokus berada. Disebut juga sumbu mayor.
- Sumbu sekunder : merupakan sumbu simetri elips yang tegak lurus sumbu utama. Ini juga disebut sumbu minor dan berhubungan dengan garis bagi tegak lurus dari segmen yang menghubungkan fokus.
- Pusat : merupakan titik potong sumbu elips. Selain itu, ini adalah pusat simetri elips (titik oranye pada grafik).
- Titik : titik potong elips dengan sumbu simetrinya (titik hitam).
- Sumbu semi mayor atau sumbu utama: ruas yang dimulai dari pusat elips sampai ke titik sumbu utama.
- Sumbu semi minor atau sumbu sekunder: ruas antara pusat elips dan simpul sumbu sekunder.
- Panjang fokus : Ini adalah jarak antara dua titik fokus.
- Jarak semi fokus : sesuai dengan jarak antara pusat dan masing-masing titik fokus.
- Vektor radio : adalah segmen yang menghubungkan setiap titik elips ke setiap fokus (segmen biru pada grafik).

Hubungan antar elemen elips
Berbagai elemen elips saling terkait satu sama lain. Selain itu, hubungan antara keduanya sangat penting untuk latihan elips, karena biasanya diperlukan untuk menyelesaikan soal elips dan menentukan persamaannya.
Seperti yang kita lihat pada definisi elips di atas, jarak dari titik mana pun pada elips ke fokus F ditambah jarak dari titik yang sama ke fokus F’ adalah konstan. Nah, nilai konstanta ini sama dengan dua kali ukuran sumbu semi mayor. Dengan kata lain, persamaan berikut berlaku untuk setiap titik pada elips:
![]()
Emas
![]()
Dan
![]()
adalah jarak dari titik P ke fokus F dan F’ masing-masing dan
![]()
adalah panjang sumbu semi-fokus.
Oleh karena itu, karena titik puncak sumbu sekunder berada tepat di tengah sumbu fokus, maka jarak titik fokus tersebut ke salah satu fokus setara dengan panjang sumbu semi primer (
![]()
):
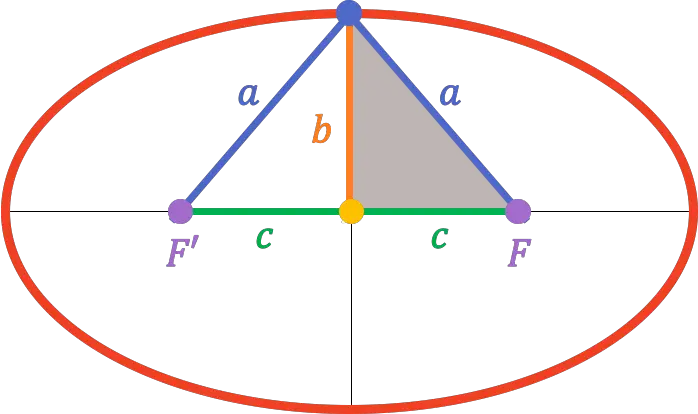
Jadi, dari teorema Pythagoras , kita dapat menemukan hubungan antara setengah sumbu utama, setengah sumbu sekunder, dan setengah panjang fokus:
![]()
Ingat rumus ini karena akan sangat berguna untuk menghitung hasil latihan dengan elips.
Eksentrisitas elips
Tentu saja, tidak semua elips itu sama, namun ada yang lebih memanjang dan ada yang lebih datar. Jadi, ada koefisien yang digunakan untuk mengukur kebulatan suatu elips. Koefisien ini disebut eksentrisitas dan dihitung dengan rumus berikut:
![]()
Emas
![]()
adalah jarak dari pusat elips ke salah satu fokusnya dan
![]()
panjang sumbu semi mayor.
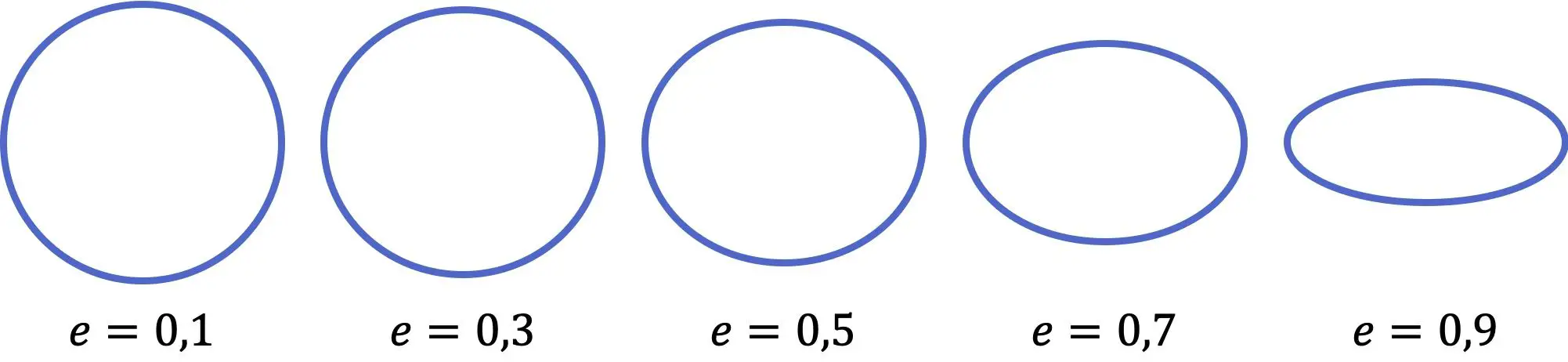
Seperti terlihat pada representasi sebelumnya, semakin kecil nilai eksentrisitas elips maka semakin menyerupai lingkaran, sebaliknya semakin besar koefisien maka elips semakin rata. Selain itu, nilai eksentrisitas berkisar dari nol (lingkaran sempurna) hingga satu (garis horizontal), keduanya tidak inklusif.

![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-4)^2}{5^2 }+\cfrac{(y-(-1))^2}{3^2} = 1\cfrac{\bm{(x-4)^2}}{\bm{25}}+\cfrac{\ bm{(y+1)^2}}{\bm{9}} \bm{= 1}

![]()
\cfrac{(x-2)^2}{6^2}+\cfrac{(y-0)^2}{3^2} = 1\cfrac{\bm{(x-2)^2}} {\bm{36}}+\cfrac{\bm{y^2}}{\bm{9}} \bm{= 1}

![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-0)^2}{13^2 }+\cfrac{(y-0)^2}{12^2} = 1\cfrac{\bm{x^2}}{\bm{169}}+\cfrac{\bm{y^2}} {\bm{144}} \bm{= 1}

![]()
d_v=6-(-4) =10 b =\cfrac{10}{2} = 5
![]()
C_x= \cfrac{10+(-4)}{2} = \cfrac{6}{2} =3 C_y= \cfrac{6+(-4)}{2} = \cfrac{2}{ 2} = 1C(3.1)
![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-3)^2}{7^2 }+\cfrac{(y-1)^2}{5^2} =1\cfrac{\bm{(x-3)^2}}{\bm{49}}+\cfrac{\bm{( y-1)^2}}{\bm{25}} \bm{= 1}
![]()
a^2=b^2+c^2 c^2=a^2-b^2 c=\sqrt{a^2-b^2} = \sqrt{7^2-5^2}=\sqrt {24}
![]()
\sqrt{24}
![]()
C(3,1) \bm{F\kiri(3+\sqrt{24},1}\kanan)} \bm{F\kiri(3-\sqrt{24},1}\kanan)}

![]()
d(P,F) + d(P,F’)= 2a 3+5= 2a 8= 2a \cfrac{8}{2}= a 4= a
![]()
a^2=b^2+c^2 b^2=a^2-c^2 b=\sqrt{a^2-c^2} = \sqrt{4^2-3^2}=\sqrt {7}
![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-0)^2}{4^2 }+\cfrac{(y-0)^2}{\left(\sqrt{7}\right)^2} =1\cfrac{\bm{x^2}}{\bm{16}}+\ cfrac{\bm{y^2}}{\bm{7}} \bm{= 1}$
Terakhir, jika artikel ini bermanfaat bagi Anda, Anda pasti juga tertarik dengan halaman kami tentang rumus hiperbola dan rumus parabola . Anda akan menemukan penjelasan detail tentang apa itu hiperbola dan parabola, persamaannya, ciri-cirinya, contohnya, latihan penyelesaiannya,…