Persamaan keliling -

Di halaman ini Anda akan menemukan segala sesuatu tentang persamaan keliling: persamaan biasa, persamaan umum, jenis persamaan keliling lainnya, kapan persamaan keliling benar,… Selain itu, Anda akan melihat contoh cara mencarinya. persamaan keliling dan Anda dapat berlatih dengan latihan yang diselesaikan.

Persamaan lingkaran biasa

Sebelum melihat apa itu persamaan keliling, mari kita ingat kembali pengertian keliling:

Keliling adalah tempat kedudukan titik-titik pada bidang yang berjarak sama terhadap suatu titik tetap yang disebut pusat.

Oleh karena itu, semua titik pada lingkaran mempunyai jarak yang sama dari pusatnya.

Selain itu, lingkaran adalah salah satu dari empat bagian berbentuk kerucut bersama dengan elips, parabola, dan hiperbola. Artinya, lingkaran dapat diperoleh dengan memotong sebuah kerucut dengan bidang yang sejajar dengan alasnya.

Cara paling sederhana untuk menggambarkan lingkaran pada bidang kartesius adalah dari persamaan biasa. Jadi, rumus persamaan keliling biasa adalah sebagai berikut:

Persamaan biasa lingkaran adalah:

$(x-a)^2+(y-b)^2=r^2$

Emas:

$r$

adalah jari-jari lingkaran.
$a$

Dan

$b$

adalah koordinat pusat lingkaran:

$C(a,b)$

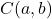
Walaupun kami tidak akan mendemonstrasikannya karena agak membosankan, namun persamaan ini dapat diperoleh dari teorema Pythagoras.

Mari kita lihat bagaimana persamaan biasa lingkaran dihitung dengan sebuah contoh:

Tentukan persamaan biasa lingkaran berjari-jari 5 yang pusatnya adalah titik
$C(3,-1).$

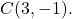
Rumus persamaan biasa lingkaran adalah:

$(x-a)^2+(y-b)^2=r^2$

Oleh karena itu, kita hanya perlu mengganti yang tidak diketahui

$r$

dengan nilai jari-jari, dan yang tidak diketahui

$a$

Dan

$b$

dengan koordinat X dan Y masing-masing dari pusat lingkaran:

$(x-3)^2+(y-(-1))^2=5^2$

Jadi persamaan lingkaran biasa adalah:

$\bm{(x-3)^2+(y+1)^2=25}$

Persamaan umum lingkaran

Jenis persamaan keliling lainnya adalah persamaan umum, bahkan persamaan ini paling banyak digunakan. Kita kemudian akan melihat bagaimana memperoleh persamaan umum keliling dari persamaan biasa.

Perhatikan persamaan biasa lingkaran:

$(x-a)^2+(y-b)^2=r^2$

Jika kita mengembangkan persamaan yang luar biasa (atau produk yang luar biasa):

$x^2+a^2-2ax+y^2+b^2-2by=r^2$

$x^2-2ax+y^2-2by+a^2+b^2-r^2=0$

Sekarang kita membuat 3 perubahan variabel:

$A=-2a \qquad B=-2b \qquad C=a^2+b^2-r^2$

Dan akhirnya kita memperoleh persamaan umum keliling:

$x^2+y^2+Ax+By+C=0$

Oleh karena itu, rumus persamaan umum keliling adalah:

$x^2+y^2+Ax+By+C=0$

dimana titik pusat lingkarannya adalah:

$\displaystyle C\left(-\frac{A}{2}, -\frac{B}{2}\right)$

Dan jari-jari lingkarannya adalah:

$\displaystyle r=\sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C}$

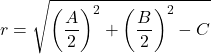
Jadi persamaan keliling ini selalu diperoleh persamaan biasa. Berikut ini contoh untuk melihat cara melakukannya:

Tentukan persamaan umum lingkaran berjari-jari 6 yang pusatnya adalah titik
$C(2,4).$

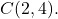
Pertama kita perlu mencari persamaan biasa lingkaran. Untuk melakukan ini, kami menggunakan rumusnya:

$(x-a)^2+(y-b)^2=r^2$

$(x-2)^2+(y-4)^2=6^2$

Dan sekarang kita operasikan sampai kita menemukan persamaan umum keliling, yaitu sampai kita tidak dapat menyederhanakan lagi:

$x^2+2^2-2\cdot x \cdot 2+y^2+4^2-2\cdot y \cdot 4=36$

$x^2+4-4x+y^2+16-8y=36$

$x^2-4x+y^2-8y+4+16-36=0$

$x^2-4x+y^2-8y-16=0$

Jadi persamaan umum lingkaran adalah:

$\bm{x^2+y^2-4x-8y-16=0}$

Meskipun soal tidak memerlukannya, sekarang kita dapat menghitung pusat dan jari-jari persamaan yang ditemukan untuk memverifikasi kebenarannya.

Untuk menentukan pusat lingkaran, kita menggunakan rumusnya:

$\displaystyle C\left(-\frac{A}{2}, -\frac{B}{2}\right)$

$\displaystyle C\left(-\frac{-4}{2}, -\frac{-8}{2}\right)$

$\displaystyle C\bigl(-(-2), -(-4)\bigr)$

$\displaystyle C\left(2,4\right)$

Faktanya, pusat lingkaran bertepatan dengan pusat pernyataan.

Kami juga memeriksa jari-jari keliling dengan rumusnya:

$\displaystyle \begin{aligned} r & = \sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C} \\[2ex] & =\sqrt{\left(\frac{-4}{2}\right)^2 +\left(\frac{-8}{2}\right)^2-(-16)} \\[2ex] & =\sqrt{\left(-2\right)^2 +\left(-4\right)^2+16} \\[2ex] &= \sqrt{4+16+16} \\[2ex] &= \sqrt{36} \\[2ex] & = 6 \end{aligned}$

Dan jari-jarinya juga sama dengan pernyataan tersebut. Oleh karena itu, persamaan keliling yang dihitung adalah benar.

Keberadaan lingkaran

Semua persamaan dalam bentuk

$x^2+y^2+Ax+By+C=0$

sesuai dengan lingkaran. Jadi, agar ekspresi seperti ini benar-benar merupakan persamaan lingkaran, 3 syarat berikut harus dipenuhi:

Koefisien dari
$x^2$

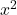
dan dari

$y^2$

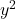
keduanya harus sama dengan 1. Ingatlah bahwa jika kedua variabel didahului oleh angka selain satu tetapi keduanya memiliki angka yang sama, seluruh persamaan dapat dibagi dengan angka tersebut sehingga koefisiennya adalah 1.
Persamaan tidak boleh mempunyai suku
$xy.$
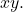
Ekspresi berikut harus positif:

Dua persamaan lingkaran yang telah kita lihat, persamaan biasa dan persamaan umum, adalah persamaan yang paling banyak digunakan untuk menyatakan lingkaran pada bidang secara matematis (dalam R2). Namun ada beberapa jenis persamaan untuk menggambarkan benda geometris tersebut, berikut penjelasan masing-masingnya.

Persamaan kanonik lingkaran

Persamaan kanonik, atau persamaan tereduksi, suatu lingkaran digunakan untuk menggambarkan setiap lingkaran yang pusatnya berada di titik asal koordinat , yaitu di titik (0,0). Persamaan tersebut adalah sebagai berikut:

$x^2+y^2=r^2$

Selain itu, jika jari-jarinya setara dengan satuan (1), maka persamaan kelilingnya adalah:

$x^2+y^2=1$

Persamaan terakhir ini berhubungan dengan keliling goniometri, disebut juga keliling satuan atau lingkaran satuan. Merupakan lingkaran berjari-jari 1 yang berpusat pada titik asal koordinat.

Persamaan dua lingkaran konsentris

Dua persamaan konsentris adalah persamaan yang mempunyai pusat di titik yang sama. Dan satu-satunya perbedaan yang dimiliki dua lingkaran konsentris adalah jari-jarinya.

Jadi agar syarat ini terpenuhi, persamaan dua lingkaran konsentris harus sama persis kecuali suku-suku bebasnya harus berbeda.

$x^2+y^2+Ax+By+C=0$

$x^2+y^2+Ax+By+C'=0$

Misalnya, dua lingkaran berikut adalah konsentris, karena semua koefisiennya identik kecuali suku-suku independennya:

$x^2+y^2+3x-4y+1=0$

$x^2+y^2+3x-4y+5=0$

Persamaan parametrik lingkaran

Seperti halnya garis, persamaan lingkaran juga dapat diparameterisasi dengan fungsi trigonometri sinus dan kosinus. Jadi, persamaan parametrik lingkaran adalah:

$\diplaystyle \begin{cases}x= a + r \cdot \text{cos}(t) \\[2ex] y= b + r\cdot \text{sen}(t)\end{cases} \qquad t\in[0,2\pi)$

dimana intinya

$(a,b)$

adalah pusat lingkaran dan

$r$

Ini adalah departemen Anda.

Menyelesaikan masalah persamaan lingkaran

Latihan 1

Hitung persamaan umum lingkaran berjari-jari 5 yang pusatnya di titik

$C(-1,2).$

lihat solusi

Untuk mencari persamaan umum lingkaran, kita harus mencari persamaan biasa lingkaran terlebih dahulu. Untuk melakukan ini, kami menggunakan rumus persamaan lingkaran biasa:

$(x-a)^2+(y-b)^2=r^2$

$(x-(-1))^2+(y-2)^2=5^2$

$(x+1)^2+(y-2)^2=25$

Setelah kita mengetahui persamaan biasa, kita bekerja sampai kita menemukan persamaan umum lingkaran:

$x^2+1^2+2\cdot x \cdot 1+y^2+2^2-2\cdot y \cdot 2=25$

$x^2+1+2x+y^2+4-4y=25$

$x^2+2x+y^2-4y+1+4-25=0$

$x^2+2x+y^2-4y-20=0$

Jadi persamaan umum lingkaran adalah:

$\bm{x^2+y^2+2x-4y-20=0}$

Latihan 2

Untuk setiap lingkaran berikut, tentukan koordinat pusatnya dan panjang jari-jarinya.

$\text{A)}\ (x-2)^2+(y+5)^2=36$

$\text{B)}\ x^2+y^2+8x-10y+1 = 0$

$\text{C)}\ x^2+y^2=4$

lihat solusi

keliling A)

$(x-2)^2+(y+5)^2=36$

Keliling dinyatakan dalam bentuk persamaan biasa yang rumusnya adalah:

$(x-a)^2+(y-b)^2=r^2$

Jadi, koordinat pusat lingkarannya adalah:

$C(a,b)$

$\bm{C(2,-5)}$

Dan radiusnya adalah:

$r^2=36$

$\bm{r=6}$

keliling B)

$x^2+y^2+8x-10y+1 = 0$

Keliling ini dinyatakan dalam bentuk persamaan umum, sehingga untuk menghitung koordinat pusatnya harus menggunakan rumus sebagai berikut:

$\displaystyle C\left(-\frac{A}{2}, -\frac{B}{2}\right)$

$\displaystyle C\left(-\frac{8}{2}, -\frac{-10}{2}\right)$

$\displaystyle C\bigl(-4, -(-5)\bigr)$

$\displaystyle \bm{C(-4, 5)}$

Sedangkan rumus mencari jari-jari lingkaran adalah:

$\displaystyle \begin{aligned} r & = \sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C} \\[2ex] & =\sqrt{\left(\frac{8}{2}\right)^2 +\left(\frac{-10}{2}\right)^2-1} \\[2ex] & =\sqrt{\left(4\right)^2 +\left(-5\right)^2-1} \\[2ex] &= \sqrt{16+25-1} \\[2ex] &= \bm{\sqrt{40}} \end{aligned}$

keliling C)

$x^2+y^2=4$

Keliling dinyatakan dalam bentuk persamaan biasa yang rumusnya adalah:

$(x-a)^2+(y-b)^2=r^2$

Jadi, koordinat pusat lingkarannya adalah:

$C(a,b)$

Dalam hal ini, persamaan tersebut tidak memiliki suku.

$a$

juga tidak

$b,$

oleh karena itu berpusat pada asal koordinat:

$\bm{C(0,0)}$

Dan radiusnya adalah:

$r^2=4$

$\bm{r=2}$

Latihan 3

Manakah persamaan berikut yang merupakan persamaan lingkaran?

$\text{A)}\ x^2+y^2+4x-6y-1=0$

$\text{B)}\ x^2+y^2+5x+5y+2xy-4 = 0$

$\text{C)}\ 2x^2+2y^2-8x+4y+2=0$

$\text{D)}\ x^2+y^2+x+2y+6=0$

lihat solusi

Agar suatu persamaan menjadi persamaan lingkaran, syarat-syarat berikut ini harus dipenuhi:

1. Koefisien dari

$x^2$

dan dari

$y^2$

Mereka harus sama dengan 1.
2. Persamaan tersebut tidak boleh mempunyai suku

$xy.$

Persamaan A)

$x^2+y^2+4x-6y-1=0$

Koefisien dari

$x^2$

Dan

$y^2$

adalah 1 dan persamaan tersebut tidak mempunyai suku

$xy.$

Oleh karena itu, cukup dengan memeriksa kondisi ketiga:

$\displaystyle \left(\frac{A}{2}\right)^2+\left(\frac{B}{2}\right)^2-C>0″ title=”Rendered by QuickLaTeX.com” height=”47″ width=”190″ style=”vertical-align: -17px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”47″ width=”216″ style=”vertical-align: -17px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”22″ width=”146″ style=”vertical-align: -5px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”103″ style=”vertical-align: -2px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”49″ style=”vertical-align: -2px;”> <p class=$ 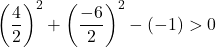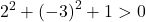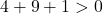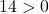Persamaan tersebut memenuhi 3 syarat, sehingga merupakan persamaan lingkaran.

Persamaan B)

$x^2+y^2+5x+5y+2xy-4 = 0$

Persamaan tersebut memiliki suku dengan

$xy,$

yang persamaannya tidak berhubungan dengan lingkaran.

Persamaan C)

$2x^2+2y^2-8x+4y+2=0$

Koefisien dari

$x^2$

Dan

$y^2$

bukan 1, tetapi kita dapat mengubah persamaan tersebut dengan membagi semua sukunya:

$x^2+y^2-4x+2y+1=0$

Dengan cara ini sekarang koefisiennya

$x^2$

Dan

$y^2$

ya, jumlahnya 1 dan, terlebih lagi, persamaan tersebut tidak memiliki suku

$xy.$

Oleh karena itu kami hanya perlu menguatkan kondisi ketiga:

$\displaystyle \left(\frac{A}{2}\right)^2+\left(\frac{B}{2}\right)^2-C>0″ title=”Rendered by QuickLaTeX.com” height=”47″ width=”190″ style=”vertical-align: -17px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”47″ width=”189″ style=”vertical-align: -17px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”22″ width=”158″ style=”vertical-align: -5px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”103″ style=”vertical-align: -2px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”42″ style=”vertical-align: -2px;”> <p class=$ 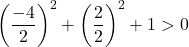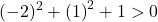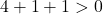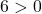Persamaan tersebut memenuhi 3 syarat, sehingga merupakan persamaan lingkaran.

Persamaan D)

$x^2+y^2+x+2y+6=0$

Koefisien dari

$x^2$

Dan

$y^2$

adalah 1 dan persamaan tersebut tidak mempunyai suku

$xy.$

Oleh karena itu, cukup dengan memeriksa kondisi ketiga:

$\displaystyle \left(\frac{A}{2}\right)^2+\left(\frac{B}{2}\right)^2-C>0″ title=”Rendered by QuickLaTeX.com” height=”47″ width=”190″ style=”vertical-align: -17px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”47″ width=”175″ style=”vertical-align: -17px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”17″ width=”128″ style=”vertical-align: -4px;”> } \ 0″ title=”Rendered by QuickLaTeX.com” height=”17″ width=”82″ style=”vertical-align: -4px;”> <p class=$ 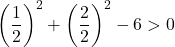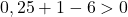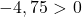Persamaan tersebut tidak memenuhi syarat terakhir, sehingga bukan persamaan lingkaran .

Latihan 4

Tentukan persamaan lingkaran yang melalui tiga titik berikut:

$A(0,0) \quad B(3,0) \quad C(2,-2)$

lihat solusi

Persamaan umum setiap lingkaran adalah:

$x^2+y^2+Ax+By+C=0$

Oleh karena itu, kita perlu mensubstitusikan koordinat titik-titik tersebut ke dalam persamaan lingkaran untuk mencari parameternya

$A,$

$B$

Dan

$C.$

Dengan poin pertama kita menemukan koefisiennya

$C:$

$A(0,0) \ \longrightarrow \ 0^2+0^2+A\cdot 0 +B\cdot 0+C=0 \ \longrightarrow \ \bm{C = 0}$

Dengan poin kedua kita menemukan koefisiennya

$A:$

$\begin{aligned}A(3,0) \ \longrightarrow \ & 3^2+0^2+A\cdot 3 +B\cdot 0+C=0 \\[2ex] & 9+A\cdot 3 =0\\[2ex]& \bm{A=-3} & \end{aligned}$

Dan dari poin ketiga kita menemukan koefisiennya

$B:$

$\begin{aligned} A(2,-2) \ \longrightarrow \ & 2^2+(-2)^2+A\cdot 2 +B\cdot (-2)+C=0 \\[2ex] & 4+4+(-3)\cdot 2+ B\cdot (-2)+0=0 \\[2ex] & 8-6-2B=0 \\[2ex] & \bm{B=1} \end{aligned}$

Kesimpulannya, persamaan umum keliling adalah:

$\bm{x^2+y^2-3x+y=0}$

Latihan 5

Jika ujung-ujung lingkaran yang berhadapan terdapat dua titik berikut:

$A(2,3) \qquad B(6,-1)$

Apa persamaan biasa lingkaran?

lihat solusi

Jika kedua titik tersebut merupakan titik ekstrem lingkaran, maka pusatnya adalah titik tengah antara dua titik berikut:

$\displaystyle C\left(\frac{2+6}{2} , \frac{3+(-1)}{2} \right)$

$\displaystyle C\left(\frac{8}{2} , \frac{2}{2} \right)$

$\displaystyle C\left(4,1 \right)$

Sebaliknya, diameter lingkaran adalah jarak antara dua titik, yang dapat dihitung dengan menggunakan besar vektor yang dibentuk kedua titik tersebut:

$\vv{AB} = B-A=(6,-1) - (2,3) = (4,-4)$

$d = \lvert \vv{AB} \rvert =\sqrt{4^2+(-4)^2} = \sqrt{16+16} = \sqrt{32}$

Dan jari-jari lingkaran adalah setengah diameternya:

$r = \cfrac{\sqrt{32}}{2}$

Oleh karena itu, persamaan biasa lingkaran adalah:

$(x-a)^2+(y-b)^2=r^2$

$\displaystyle (x-4)^2+(y-1)^2=\left(\frac{\sqrt{32}}{2}\right)^2$

$\displaystyle \bm{(x-4)^2+(y-1)^2=}\frac{\bm{32}}{\bm{4}}$

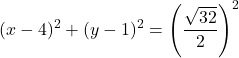
Terakhir, jika artikel ini bermanfaat bagi Anda, Anda pasti juga tertarik dengan halaman hiperbola (matematika) dan parabola (matematika) kami. Anda akan menemukan penjelasan rinci tentang apa itu hiperbola dan parabola, persamaannya, ciri-cirinya, contohnya, latihan penyelesaiannya…

Persamaan lingkaran biasa

Persamaan umum lingkaran

Keberadaan lingkaran

Persamaan kanonik lingkaran

Persamaan dua lingkaran konsentris

Persamaan parametrik lingkaran

Menyelesaikan masalah persamaan lingkaran

Latihan 1

Latihan 2

Latihan 3

Latihan 4

Latihan 5

Tinggalkan Komentar Batalkan Balasan