Di sini Anda akan menemukan rumus yang digunakan untuk menghitung jarak antara titik dan garis. Selain itu, Anda akan dapat melihat beberapa contoh dan menyelesaikan latihan jarak antara titik dan garis dan, bahkan, penerapan operasi ini (misalnya, mencari jarak antara garis sejajar).
Rumus jarak antara titik dan garis
Jarak antara suatu titik dan suatu garis adalah jarak terpendek antara titik tersebut dan garis tersebut. Secara matematis, jarak minimum ini setara dengan panjang ruas yang ditarik dari titik ke garis dan tegak lurus garis.
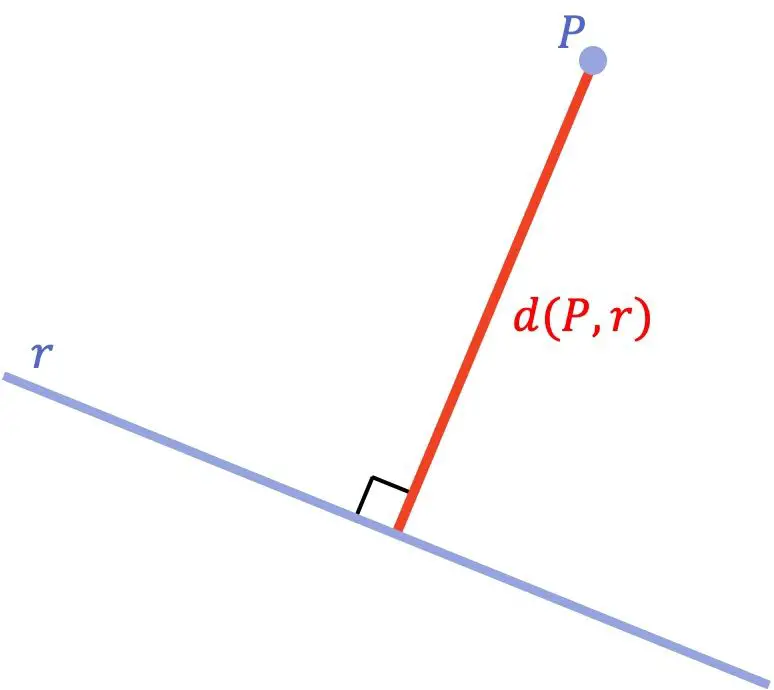
Setelah kita melihat konsep geometri jarak antara titik dan garis, mari kita lihat rumus apa yang digunakan untuk menghitung jarak tersebut:
Mengingat persamaan implisit (atau umum) dari sebuah garis dan koordinat titik mana pun pada bidang:
![]()
Rumus jarak antara titik dan garis adalah:
![]()
Penting: Perhatikan bahwa persamaan garis dalam rumusnya berbentuk persamaan implisit (atau umum), jadi jika kita mempunyai garis yang dinyatakan dalam persamaan jenis lain, kita harus meneruskannya terlebih dahulu ke persamaan implisitnya, lalu kita bisa menerapkan rumusnya.
Contoh menghitung jarak antara titik dan garis
Di bawah ini Anda dapat melihat contoh penghitungan jarak antara titik dan garis:
- Temukan jarak antara titik tersebut

dan hukum

![]()
Untuk menghitung jarak antara titik dan garis, cukup terapkan rumusnya:
![]()
Sekarang kita ganti setiap suku dengan nilainya:
![]()
Dan terakhir kita hitung jaraknya:
![]()
Jarak antara dua garis sejajar
Salah satu penerapan penghitungan jarak suatu garis ke suatu titik adalah dengan mencari jarak antara garis-garis sejajar.
Tentunya untuk memahami konsep yang akan kami jelaskan di bawah ini anda harus mengetahui apa itu garis sejajar , jadi jika anda belum mengetahui secara pasti definisinya, kami tinggalkan link yang akan kami jelaskan secara detail dan anda juga bisa melihat contohnya. dari garis sejajar.
Untuk mencari jarak antara dua garis sejajar, cukup ambil sebuah titik pada salah satu dari dua garis tersebut dan hitung jarak dari titik tersebut ke garis lainnya.

Jadi, untuk menentukan jarak antara dua garis sejajar digunakan juga rumus jarak antara suatu garis dan suatu titik.
Sebaliknya, jika dengan menggunakan rumus diperoleh jarak 0 satuan, berarti garis-garis tersebut saling bersentuhan di suatu titik sehingga garis-garis tersebut tidak sejajar, melainkan berpotongan, berhimpitan, atau tegak lurus. Jika mau, Anda dapat memeriksa perbedaan jenis garis ini di website kami.
Jadi mari kita lihat bagaimana menyelesaikan masalah jarak antara dua garis sejajar melalui sebuah contoh:
- Tentukan jarak antara dua garis sejajar berikut:
![]()
Hal pertama yang perlu kita lakukan adalah mendapatkan titik pada salah satu garis (yang Anda inginkan). Dalam hal ini, kita akan menghitung sebuah titik pada garis
![]()
Untuk melakukan ini, Anda harus memberi nilai pada salah satu variabel, misalnya akan kita lakukan
![]()
![]()
Dan sekarang kita menghapus variabel lainnya (
![]()
) dari persamaan yang diperoleh untuk mengetahui berapa nilainya pada saat ini:
![]()
![]()
![]()
Oleh karena itu, titik diperoleh dari garis tersebut
![]()
Timur:
![]()
Dan ketika kita sudah mempunyai sebuah titik pada sebuah garis, kita menghitung jarak dari titik tersebut ke garis lainnya dengan menggunakan rumus:
![]()
![]()
Menyelesaikan masalah jarak antara titik dan garis
Latihan 1
Hitung jarak antar titik
![]()
dan hukum
![]()
![]()
Untuk mencari jarak antara titik dan garis, cukup terapkan rumusnya:
![]()
Kami mengganti setiap suku dengan nilainya dan menghitung jaraknya:
![]()
Latihan 2
Berapa jarak antar titik tersebut
![]()
dan hukum
![]()
?
![]()
Dalam hal ini, persamaan garis berbentuk implisit (atau umum). Sebaliknya, untuk menggunakan rumus jarak suatu titik ke garis, garis tersebut harus dinyatakan sebagai persamaan implisit. Oleh karena itu, pertama-tama kita harus mengubah garis tersebut dan meneruskannya ke persamaan implisit (lewati saja semua suku pada sisi persamaan yang sama):
![]()
Dan jika garis sudah dalam bentuk eksplisit, sekarang kita dapat menggunakan rumus jarak antara titik dan garis:
![]()
Oleh karena itu, kami mengganti setiap suku dengan nilainya dan menghitung jaraknya:
![]()
Latihan 3
Berapa jarak antara dua garis berikut?
![]()
Pertama, kita akan memverifikasi bahwa ini adalah dua garis sejajar. Untuk ini, koefisien variabel
![]()
Dan
![]()
harus proporsional satu sama lain tetapi tidak dengan ketentuan independen:
![]()
Memang garisnya sejajar, oleh karena itu kita dapat menerapkan prosedur tersebut.
Sekarang kita perlu mendapatkan titik dari salah satu garis (yang Anda inginkan). Dalam hal ini, kita akan menghitung sebuah titik pada garis
![]()
Untuk melakukan ini, Anda harus menetapkan nilai ke salah satu variabel, misalnya yang akan kami lakukan
![]()
![]()
Dan sekarang kita menghapus variabel lainnya (
![]()
) dari persamaan yang diperoleh untuk mengetahui nilainya pada titik ini:
![]()
![]()
![]()
Sehingga diperoleh titik dari garis tersebut
![]()
Timur:
![]()
Setelah kita mengetahui suatu titik pada suatu garis, kita menghitung jarak dari titik tersebut ke garis lainnya dengan rumus:
![]()
![]()
Latihan 4
Hitung nilai yang tidak diketahui
![]()
sehingga jarak antar titik
![]()
dan hukum
![]()
yaitu 5 unit.
![]()
Pertama-tama kita harus menerapkan rumus jarak antara titik dan garis:
![]()
Sekarang kita ganti setiap suku dengan nilainya dan sederhanakan ekspresi:
![]()
Rumusan masalah memberitahu kita bahwa jarak antara titik dan garis harus sama dengan 5, jadi persamaan sebelumnya sama dengan 5:
![]()
Dan kami menyelesaikan persamaan yang dihasilkan. Pada pembilang pecahan terdapat nilai mutlak, oleh karena itu kita harus menganalisis secara terpisah kapan nilai mutlaknya positif dan kapan negatif:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Oleh karena itu, ada dua kemungkinan nilai
![]()
benar:
![]()
salah satu
![]()