Persamaan titik – kemiringan garis

Di halaman ini, Anda akan menemukan rumus persamaan titik-kemiringan garis dan juga berbagai cara untuk menghitungnya. Selain itu, Anda akan dapat melihat beberapa contoh dan latihan dengan latihan yang diselesaikan langkah demi langkah.

Rumus persamaan titik-kemiringan garis

Persamaan titik-kemiringan suatu garis adalah cara untuk menyatakan suatu garis secara matematis. Secara khusus, Anda hanya memerlukan kemiringan dan koordinat suatu titik pada garis untuk mencari persamaan titik-kemiringan suatu garis.

Rumus persamaan titik-kemiringan garis adalah sebagai berikut:

$y-y_0=m(x-x_0)$

Emas

$m$

adalah kemiringan garis dan

$x_0, y_0$

adalah koordinat suatu titik pada garis

$P(x_0,y_0).$

Mari kita lihat bagaimana persamaan titik-kemiringan garis dihitung dengan menggunakan contoh:

Tuliskan persamaan titik-kemiringan garis yang melalui titik tersebut
$P(2,-1)$

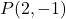
dan kemiringan m=3.

Rumus persamaan titik-kemiringan garis adalah sebagai berikut:

$y-y_0=m(x-x_0)$

Dalam hal ini, pernyataan tersebut menyatakan bahwa kemiringan garis adalah m=3, sehingga persamaan garisnya adalah sebagai berikut:

$y-y_0=3(x-x_0)$

Selanjutnya kita juga mengetahui bahwa garis melalui suatu titik

$P(2,-1)$

, oleh karena itu kita harus mensubstitusikan koordinat titik ini ke dalam persamaan:

$P(2,-1)$

$y-y_0=3(x-x_0) \ \xrightarrow{x_0=2 \ ; \ y_0=-1} \ y-(-1)=3(x-2)$

Oleh karena itu, persamaan titik-kemiringan garis tersebut adalah:

$\bm{y+1=3(x-2)}$

Ingatlah bahwa selain persamaan titik-kemiringan, ada cara lain untuk menyatakan garis secara analitis: persamaan vektor, persamaan parametrik, persamaan kontinu, persamaan implisit (atau umum) dan persamaan garis eksplisit. Jika Anda lebih tertarik, Anda dapat memeriksa masing-masingnya di situs web kami.

Apa yang dimaksud dengan kemiringan suatu garis?

Seperti yang kita lihat pada definisi persamaan titik-kemiringan suatu garis, parameternya

$m$

adalah kemiringan garis. Tapi sungguh… apa yang dimaksud dengan kemiringan suatu garis? Mari kita lihat ini dari representasi grafis sebuah garis:

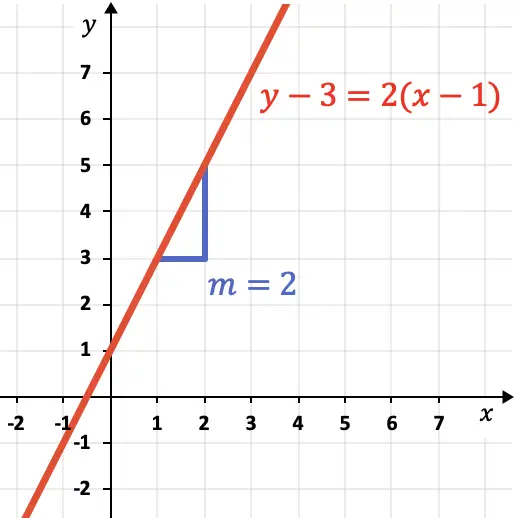
Apa persamaan titik-kemiringan suatu garis?

Kemiringan garis menunjukkan kecuramannya. Seperti yang Anda lihat dari garis grafik,

$m$

sama dengan 2 karena garis naik 2 satuan vertikal untuk 1 satuan horizontal.

Jelasnya, jika kemiringannya positif maka fungsinya bertambah (naik), sebaliknya jika kemiringannya negatif maka fungsinya menurun (turun).

Cara menghitung kemiringan suatu garis

Selain itu, ada 3 cara berbeda untuk menentukan kemiringan suatu garis secara numerik:

Diberikan dua titik berbeda pada garis tersebut
$P_1(x_1,y_1)$

Dan

$P_2(x_2,y_2),$

Kemiringan garis sama dengan:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}$

Ya
$\vv{\text{v}}= (\text{v}_1,\text{v}_2)$

adalah vektor arah garis, kemiringannya adalah:

$m = \cfrac{\text{v}_2}{\text{v}_1}$

Ya
$\alpha$

adalah sudut yang dibentuk oleh garis dengan sumbu absis (sumbu X), kemiringan garis tersebut ekuivalen dengan garis singgung sudut tersebut:

$m = \text{tg}(\alpha )$

Posisi relatif garis

Terakhir, kemiringan suatu garis juga digunakan untuk mengetahui hubungan beberapa garis. Karena dua garis sejajar mempunyai kemiringan yang sama, dan sebaliknya jika kemiringan suatu garis merupakan kebalikan negatif dari kemiringan garis yang lain, maka kedua garis tersebut tegak lurus .

garis sejajar dengan kemiringan yang sama

Hitung persamaan titik-kemiringan garis yang melalui dua titik

Masalah yang sangat umum adalah menentukan persamaan titik-kemiringan dari dua titik yang termasuk dalam garis. Mari kita lihat bagaimana penyelesaiannya melalui sebuah contoh:

Tentukan persamaan titik-kemiringan garis yang melalui dua titik berikut:

$P_1(5,2) \qquad P_2(3,6)$

Untuk mencari persamaan titik-kemiringan suatu garis, kita perlu menentukan kemiringan garis tersebut. Jadi kita menghitung kemiringan garis menggunakan rumus titik dua:

$m =\cfrac{\Delta y}{\Delta x}=\cfrac{y_2-y_1}{x_2-x_1} = \cfrac{6-2}{3-5} = \cfrac{4}{-2}= -2$

Jadi, persamaan titik-kemiringan garis tersebut adalah sebagai berikut:

$y-y_0=m(x-x_0)$

$y-y_0=-2(x-x_0)$

Oleh karena itu, kita hanya perlu mensubstitusikan koordinat kartesius suatu titik pada garis tersebut ke dalam persamaan:

$P_1(5,2)$

$y-y_0=-2(x-x_0) \ \xrightarrow{x_0=5 \ ; \ y_0=2} \ y-2=-2(x-5)$

$\bm{y-2=-2(x-5)}$

Ada baiknya juga jika kita masukkan poin lain dari pernyataan tersebut ke dalam persamaan garis:

$P_1(3,6)$

$y-6=-2(x-3)$

Temukan persamaan titik-kemiringan suatu garis dari grafik

Seperti yang kita lihat pada bagian di atas, ada beberapa cara untuk mencari persamaan titik-kemiringan suatu garis secara numerik. Namun, hal ini juga dapat ditemukan secara grafis. Mari kita lihat bagaimana hal ini dilakukan melalui sebuah contoh:

Tentukan persamaan titik-kemiringan garis yang ditunjukkan pada grafik berikut:

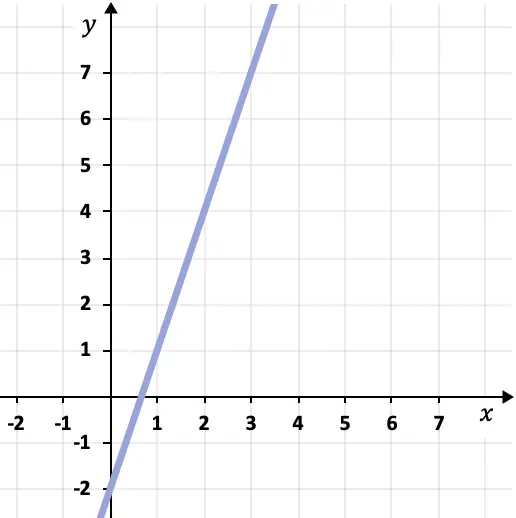
Untuk menentukan persamaan titik-kemiringan garis yang ditarik, kita perlu mencari kemiringan dan titik pada garis tersebut.

Dalam hal ini kemiringan garis sama dengan 3, karena garis naik 3 satuan vertikal untuk setiap satuan horizontal.

$m = 3$

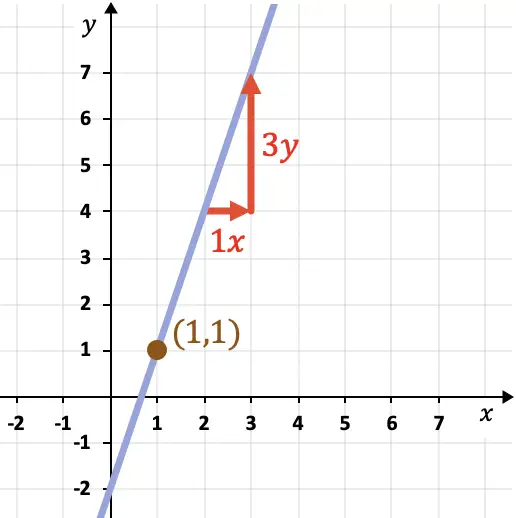
Selanjutnya kita memerlukan sebuah titik pada garis tersebut. Untuk melakukan ini, kita dapat memilih titik mana saja pada grafik yang dilalui garis, misalnya titik (1,1).

$P(1,1)$

Oleh karena itu, sekarang kita dapat mencari persamaan titik-kemiringan garis dengan menerapkan rumusnya:

$y-y_0=m(x-x_0)$

$y-1=3(x-1)$

menentukan secara grafis kemiringan titik persamaan suatu garis

Menyelesaikan Masalah Persamaan Titik-Kemiringan

Latihan 1

Tuliskan persamaan titik-kemiringan garis yang melalui titik tersebut

$P(1,4)$

dan kemiringannya adalah

$m=-2.$

lihat solusi

Rumus persamaan titik-kemiringan garis adalah:

$y-y_0=m(x-x_0)$

Dalam hal ini pernyataan tersebut menyatakan bahwa kemiringan garis adalah m=-2, sehingga persamaan garisnya adalah sebagai berikut:

$y-y_0=-2(x-x_0)$

Selanjutnya kita juga mengetahui dari pernyataan bahwa garis melalui suatu titik

$P(1,4)$

, oleh karena itu cukup dengan mensubstitusikan koordinat titik tersebut ke dalam persamaan garis:

$P(1,4)$

$\bm{y-4=-2(x-1)}$

Latihan 2

Berapakah persamaan titik-kemiringan garis yang melalui dua titik berikut?

$P_1(1,6) \qquad P_2(4,0)$

lihat solusi

Untuk mencari persamaan titik-kemiringan suatu garis, kita perlu menentukan kemiringan garis tersebut. Oleh karena itu kami menghitung kemiringan garis dengan rumusnya:

$m =\cfrac{\Delta y}{\Delta x}=\cfrac{y_2-y_1}{x_2-x_1} = \cfrac{0-6}{4-1} = \cfrac{-6}{3}= -2$

Jadi, persamaan titik-kemiringan garis tersebut adalah sebagai berikut:

$y-y_0=m(x-x_0)$

$y-y_0=-2(x-x_0)$

Oleh karena itu, kita hanya perlu mensubstitusikan koordinat suatu titik pada garis tersebut ke dalam persamaan:

$P_1(1,6)$

$\bm{y-6=-2(x-1)}$

Benar juga jika poin lain dari pernyataan tersebut dimasukkan ke dalam persamaan:

$y=-2(x-4)$

Latihan 3

Tentukan persamaan titik-kemiringan garis yang melalui dua titik berikut:

$P_1(1,-2) \qquad P_2(2,3)$

lihat solusi

Untuk mencari persamaan titik-kemiringan suatu garis, Anda harus menghitung kemiringannya terlebih dahulu:

$m =\cfrac{\Delta y}{\Delta x}=\cfrac{y_2-y_1}{x_2-x_1} = \cfrac{3-(-2)}{2-1} = \cfrac{3+2}{1}=\cfrac{5}{1}= 5$

Jadi, persamaan titik-kemiringan garis tersebut adalah sebagai berikut:

$y-y_0=m(x-x_0)$

$y-y_0=5(x-x_0)$

Oleh karena itu, kita hanya perlu mensubstitusikan koordinat suatu titik pada garis tersebut ke dalam persamaan:

$P_1(1,-2)$

$y-(-2)=5(x-1)$

$\bm{y+2=5(x-1)}$

Benar juga jika titik lain dalam pernyataan tersebut dimasukkan ke dalam persamaan garis:

$y-3=5(x-2)$

Latihan 4

Hitung persamaan titik-kemiringan garis yang membentuk sudut 45º terhadap sumbu X dan melalui titik asal koordinat.

lihat solusi

Jika garis membentuk sudut 45 derajat terhadap sumbu OX, kemiringannya adalah:

$m = \text{tg}(45º) = 1$

$y-y_0=1(x-x_0)$

$y-y_0=x-x_0$

Dan setelah kita mengetahui kemiringan garis, kita dapat mencari persamaan titik-kemiringan dengan mensubstitusikan sebuah titik pada garis ke dalam persamaan tersebut. Selain itu, pernyataan tersebut menyatakan bahwa garis melalui titik asal koordinat, yang berarti melalui titik (0,0). Belum:

$P(0,0)$