Di halaman ini, Anda akan menemukan segala sesuatu tentang persamaan garis secara eksplisit: apa itu persamaan garis, apa rumusnya, contoh perhitungannya, dll. Anda juga akan menemukan penjelasan rinci tentang arti kemiringan dan titik potong persamaan eksplisit. Dan terlebih lagi, Anda akan melihat berbagai contoh dan Anda akan dapat berlatih dengan latihan yang diselesaikan langkah demi langkah.
Apa persamaan garis yang jelas?
Ingatlah bahwa definisi matematis garis adalah sekumpulan titik berurutan yang direpresentasikan dalam arah yang sama tanpa kurva atau sudut.
Jadi, persamaan garis eksplisit adalah cara untuk menyatakan garis apa pun secara matematis. Untuk melakukannya, Anda hanya perlu mengetahui kemiringan garis dan titik potong sumbu Y.
Rumus persamaan garis eksplisit
Rumus persamaan garis eksplisit adalah:
![]()
Emas
![]()
adalah kemiringan garis dan
![]()
perpotongannya dengan sumbu Y, yaitu ketinggian perpotongannya dengan sumbu Y.
Mari kita lihat bagaimana persamaan garis eksplisit dihitung melalui contoh:
- Tuliskan persamaan garis yang melalui titik tersebut
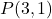
dan kemiringan m=2.
Rumus persamaan garis eksplisit adalah:
![]()
Dalam hal ini, pernyataan tersebut menyatakan bahwa kemiringan garis adalah m=2, sehingga persamaan garisnya adalah sebagai berikut:
![]()
Oleh karena itu cukup menghitung koefisien n. Untuk melakukan ini, kita harus mensubstitusikan sebuah titik yang termasuk dalam garis ke dalam persamaannya. Dan dalam hal ini, pernyataan tersebut memberitahu kita bahwa garis melalui suatu titik
![]()
Belum:
![]()
![]()
Dan kita selesaikan persamaan yang dihasilkan untuk mencari nilai n:
![]()
![]()
![]()
![]()
Oleh karena itu, persamaan garis yang jelas adalah:
![]()
Ingatlah bahwa selain persamaan eksplisit, ada cara lain untuk menyatakan garis secara analitis. Misalnya persamaan vektor , yaitu jenis persamaan garis yang berbeda dengan persamaan garis lainnya karena vektor arah dan suatu titik pada garis dinyatakan dengan koordinatnya masing-masing. Di tautan Anda dapat melihat apa itu dan mengapa ini begitu istimewa.
Arti parameter m dan n
Seperti yang kita lihat pada definisi persamaan garis eksplisit, parameter
![]()
adalah kemiringan garis dan
![]()
perpotongan y-nya. Tapi apa maksudnya? Mari kita lihat ini dari representasi grafis sebuah garis:

Istilahnya mandiri
![]()
adalah titik potong garis dengan sumbu komputer (sumbu OY). Pada grafik di atas
![]()
sama dengan 1 karena garis tersebut memotong sumbu y di y=1.
Di sisi lain, istilah tersebut
![]()
menunjukkan kemiringan garis , yaitu kemiringannya. Seperti yang Anda lihat pada grafik,
![]()
sama dengan 2 karena garis naik 2 satuan vertikal untuk 1 satuan horizontal.
Jelasnya, jika kemiringannya positif maka fungsinya bertambah (naik), sebaliknya jika kemiringannya negatif maka fungsinya menurun (turun).
Menghitung kemiringan suatu garis
Selain itu, ada 3 cara berbeda untuk menentukan kemiringan suatu garis secara numerik:
- Diberikan dua titik berbeda pada garis tersebut

Dan

Kemiringan garis sama dengan:
- Ya

adalah vektor arah garis, kemiringannya adalah:
- Ya

adalah sudut yang dibentuk oleh garis dengan sumbu absis (sumbu X), kemiringan garis tersebut ekuivalen dengan garis singgung sudut tersebut:
![]()
![]()
![]()

Posisi relatif garis
Terakhir, kemiringan suatu garis juga digunakan untuk mengetahui hubungan beberapa garis. Karena dua garis sejajar mempunyai kemiringan yang sama, dan sebaliknya jika kemiringan suatu garis merupakan kebalikan negatif dari kemiringan garis yang lain, maka kedua garis tersebut tegak lurus .


Hitung persamaan eksplisit garis yang melalui dua titik
Masalah yang sangat umum adalah menemukan persamaan eksplisit sebuah garis dengan dua titik yang dilaluinya. Mari kita lihat bagaimana penyelesaiannya melalui sebuah contoh:
- Tentukan persamaan garis yang melalui dua titik berikut:
![]()
Untuk mencari persamaan garis yang jelas, Anda perlu mengetahui nilai parameter m dan n. Jadi kita hitung dulu kemiringan garisnya menggunakan rumus titik dua:
![]()
![]()
Lalu kita dapat mencari titik potong y dengan mensubstitusikan sebuah titik pada garis ke dalam persamaan:
![]()
![]()
![]()
![]()
![]()
Jadi persamaan garisnya secara eksplisit adalah:
![]()
Menemukan persamaan eksplisit dari persamaan implisit
Terakhir, jenis soal lain yang sering kita temui adalah mencari persamaan garis eksplisit dari persamaan implisitnya (disebut juga persamaan umum atau persamaan kartesius). Tentunya, untuk memahami metode berikut ini Anda perlu mengetahui secara pasti apa persamaan yang tersirat dan bagaimana persamaannya; namun jika anda tidak ingat sama sekali anda bisa mengeceknya di link tersebut.
Jadi, jika Anda sudah menguasai persamaan garis implisit (atau umum), mari kita lihat cara kerja prosedur ini:
- Temukan persamaan eksplisit dari baris berikut:
![]()
Yang harus kita lakukan untuk menemukan persamaan garis eksplisit adalah dengan menyelesaikan variabelnya
![]()
Jadi kami melewati persyaratan tanpa
![]()
di sisi lain persamaan:
![]()
Sekarang kita menghapus variabelnya
![]()
![]()
Dan terakhir, kami sederhanakan:
![]()
![]()
![]()
Oleh karena itu, kemiringan garis ini adalah
![]()
dan titik potong y-nya adalah 4.
Memecahkan Masalah Persamaan Eksplisit
Latihan 1
Tentukan kemiringan dan perpotongan y dari garis berikut:
![Rendered by QuickLaTeX.com \begin{array}{lll} A) \ y= 3x-1 & \qquad & B) \ y=5x+2 \\[2ex] C) \ y=-x+3 & \qquad & D) \ 4x+2y-6=0 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3077643710747855c7b59a93551fbad8_l3.png)
Persamaan eksplisit suatu garis mengikuti rumus berikut:
![]()
Emas
![]()
adalah kemiringan dan
![]()
komputer di tempat asal. Belum:
![Rendered by QuickLaTeX.com \bm{A)} \ y= 3x-1 \ \begin{cases} m = 3 \\[2ex] n=-1\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f62bc45bc23ea6c323b1a5d95ba40ca2_l3.png)
![Rendered by QuickLaTeX.com \bm{B)} \ y= 5x+2 \ \begin{cases} m = 5 \\[2ex] n=2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-683f74baf43275be7565fc744704e6ed_l3.png)
![Rendered by QuickLaTeX.com \bm{C)} \ y= -x+3 \ \begin{cases} m = -1 \\[2ex] n=3\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-39e8a1c6dbe8e5ff8db1fc8b08c4c95d_l3.png)
Baris terakhir dinyatakan dengan persamaan implisitnya, jadi pertama-tama kita harus meneruskannya ke persamaan eksplisit (pecahkan
![]()
) maka kita dapat mengidentifikasi parameternya:
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{cases} m = -2 \\[2ex] n=3 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-50c2bb75ae362e0a2dee3a3670459df3_l3.png)
Latihan 2
Temukan persamaan eksplisit garis yang melalui titik tersebut
![]()
dan memiliki kemiringan
![]()
Rumus persamaan garis eksplisit adalah:
![]()
Dalam hal ini kemiringan garis harus -2, sehingga persamaan garisnya berbentuk sebagai berikut:
![]()
Oleh karena itu cukup menghitung koefisien n. Untuk melakukan ini, Anda harus mengganti titik milik garis ke dalam persamaannya dan menyelesaikan persamaan yang dihasilkan:
![]()
![]()
![]()
![]()
![]()
Singkatnya, persamaan garis eksplisitnya adalah:
![]()
Latihan 3
Tentukan persamaan garis yang melalui dua titik berikut:
![]()
Untuk mencari persamaan garis yang jelas, Anda perlu mengetahui nilai parameter m dan n. Oleh karena itu, pertama-tama kita menghitung kemiringan garis dari koordinat kedua titik tersebut:
![]()
![]()
Dan kemudian kita menentukan titik potong dengan mensubstitusikan sebuah titik pada garis ke dalam persamaan:
![]()
![]()
![]()
![]()
Jadi persamaan garisnya secara eksplisit adalah:
![]()
Latihan 4
Hitung persamaan eksplisit garis yang membentuk sudut 45º terhadap sumbu X dan melalui titik asal koordinat.
Jika garis membentuk sudut 45 derajat terhadap sumbu OX, kemiringannya adalah:
![]()
![]()
Dan setelah kita mengetahui kemiringan garis, kita dapat menghitung titik potong y dengan memasukkan sebuah titik pada garis ke dalam persamaan. Selain itu, pernyataan tersebut menyatakan bahwa garis melalui titik asal koordinat, yang berarti melalui titik (0,0). Belum:
![]()
![]()
![]()
Jadi persamaan garisnya secara eksplisit adalah:
![]()
Latihan 5
Temukan persamaan eksplisit garis yang sejajar dengan garis tersebut
![]()
dan apa yang terjadi di titik tersebut
![]()
menjadi lurus
![]()
![]()
Sehingga garis tersebut sejajar dengan garis
![]()
keduanya harus mempunyai kemiringan yang sama, oleh karena itu:
![]()
![]()
Dan setelah kita mengetahui kemiringan garis, kita dapat menghitung perpotongan y dengan mensubstitusikan titik yang termasuk dalam garis tersebut ke dalam persamaan:
![]()
![]()
![]()
![]()
![]()
Jadi persamaan garisnya secara eksplisit adalah:
![]()
Latihan 6
Apa persamaan eksplisit dari setiap garis grafik?

biru benar
Garis biru bertambah satu Y untuk masing-masingnya
![]()
hijau kanan
Garis hijau bertambah 3 Ys untuk setiap X, jadi kemiringannya adalah 3. Selain itu, garis tersebut memotong sumbu Y di -4, sehingga perpotongan y-nya adalah -4.
![]()
garis merah
Garis merah berkurang dua Y untuk setiap X, sehingga kemiringannya adalah -2. Dan garis tersebut memotong sumbu y di y=-2, jadi perpotongan y-nya juga -2.
![]()