Pada artikel ini kami akan menjelaskan apa itu asimtot miring suatu fungsi. Anda akan mempelajari kapan suatu fungsi memiliki asimtot miring dan cara menghitungnya. Dan, sebagai tambahan, Anda akan dapat melihat contoh asimtot miring dan berlatih dengan latihan yang diselesaikan langkah demi langkah.
Apa yang dimaksud dengan asimtot miring?
Asimtot miring suatu fungsi adalah garis miring yang grafiknya mendekati tak terhingga tanpa pernah melintasinya. Akibatnya, semua asimtot miring adalah garis dengan persamaan y=mx+n .
Kemiringan dan titik asal asimtot miring dihitung menggunakan rumus berikut:
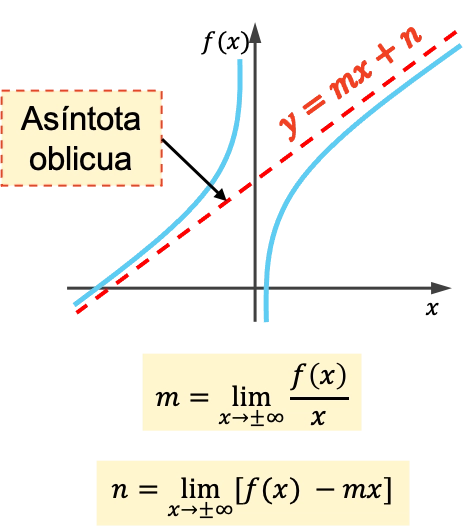
Cara menghitung asimtot miring suatu fungsi
Untuk menghitung asimtot miring suatu fungsi, langkah-langkah berikut harus dilakukan:
- Hitung limit hingga tak terhingga dari fungsi tersebut dibagi x.
- Jika limit di atas menghasilkan bilangan real bukan nol, berarti fungsi tersebut mempunyai asimtot miring. Terlebih lagi, kemiringan asimtot miring tersebut akan menjadi nilai yang diperoleh pada batasnya.
- Dalam hal ini, yang tersisa hanyalah menghitung titik potong asimtot miring dengan menyelesaikan limit berikut:
![]()
![]()
Catatan: limit harus dihitung pada plus dan minus tak terhingga, tetapi biasanya memberikan hasil yang sama dan itulah sebabnya kita menyederhanakannya dengan memasukkan ±∞. Namun jika batas plus dan minus tak terhingga berbeda, asimtot miring kiri dan asimtot miring kanan harus dihitung secara terpisah.
Contoh Asimtot Miring
Selanjutnya, kita akan mengambil asimtot miring dari fungsi rasional berikut sehingga Anda dapat melihat contoh cara melakukannya:
![]()
Asimtot miring termasuk dalam tipe ini
![]()
Jadi kita hitung dulu kemiringan garisnya
![]()
dengan rumus yang sesuai:
![]()
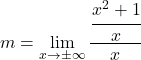
Untuk menyelesaikan limit ini kita harus menerapkan sifat-sifat pecahan:
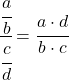
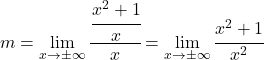
Dan sekarang kita menghitung batasnya:
![]()
Dalam hal ini, hasil dari ketidakterbatasan antara tak terhingga adalah pembagian koefisien x pangkat tertinggi, karena pembilang dan penyebutnya berorde sama.
Limit di atas menghasilkan bilangan real bukan nol, sehingga fungsi tersebut mempunyai asimtot miring. Sekarang kita akan menghitung perpotongan y
![]()
dari asimtot menggunakan rumus yang sesuai:
![]()
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-1x\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-9197669cc0e41aa22224b552b21b31ed_l3.png)
Kami mencoba menghitung batasnya:
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-x\right] = \cfrac{+\infty}{+\infty} - (+\infty) = \bm{+\infty - \infty}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4d7fa012eace37e82c243012c91f1a5c_l3.png)
Tapi kita mendapatkan ketidakterbatasan tak terhingga dikurangi tak terhingga. Oleh karena itu, suku-suku tersebut perlu direduksi menjadi penyebut yang sama. Untuk melakukannya, kita mengalikan dan membagi x dengan penyebut pecahan:
![Rendered by QuickLaTeX.com \displaystyle n=\lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x\cdot x}{x} \right] = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x^2}{x}\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-a2355ed9411470b9fd20a50ebbd48726_l3.png)
Karena kedua suku tersebut memiliki penyebut yang sama, kita dapat mengelompokkannya:
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x^2}{x} \right] = \lim_{x \to \pm\infty} \cfrac{x^2+1-x^2}{x}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f932ebc8728669c7c6b57e115c444fc7_l3.png)
Kami beroperasi pada pembilang:
![]()
Dan akhirnya, kami menyelesaikan batasannya:
![]()
Jadi n =0. Oleh karena itu, asimtot miring adalah fungsi linier:
![]()
![]()
![]()
Fungsi yang dipelajari ditunjukkan pada grafik di bawah ini. Seperti yang Anda lihat, fungsinya sangat dekat dengan garis y=x tetapi tidak pernah menyentuhnya karena merupakan asimtot miring:

Latihan terpecahkan pada asimtot miring
Latihan 1
Temukan asimtot miring dari fungsi rasional berikut:
![]()
Asimtot miring berbentuk
![]()
, oleh karena itu perlu untuk menghitung parameter m dan n . Pertama-tama kita menghitung m dengan menerapkan rumusnya:
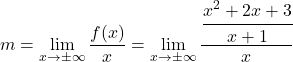
Kita menyederhanakan pecahan dengan menerapkan sifat-sifat pecahan:
![]()
![]()
Dan kami memecahkan batasnya:
![]()
Jadi m =1. Sekarang mari kita hitung titik potong asimtot miring dengan menerapkan rumusnya:
![]()
Kami mencoba menghitung batasnya:
![]()
Tapi kita mendapatkan bentuk tak tentu tak terhingga dikurangi tak terhingga. Oleh karena itu, kita harus mereduksi suku-suku tersebut menjadi penyebut yang sama dan kemudian mengelompokkannya:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle n = \lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-x\right] =\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-\frac{x \cdot (x+1)}{x+1} \right] = \\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-\frac{x^2+x}{x+1} \right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \frac{x^2+2x+3-(x^2+x)}{x+1}\\[6ex]\displaystyle =\lim_{x \to \pm\infty} \frac{x^2+2x+3-x^2-x}{x+1}=\\[6ex]=\displaystyle \lim_{x \to \pm\infty} \frac{x+3}{x+1}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0712d34ed442d9e12ef2490f04df078a_l3.png)
Dan akhirnya, kami menyelesaikan batasannya:
![]()
Singkatnya, asimtot miring dari fungsi tersebut adalah:
![]()
![]()
![]()
Latihan 2
Temukan semua asimtot miring dari fungsi rasional berikut:
![]()
Pertama, kita menggunakan rumus kemiringan asimtot miring:
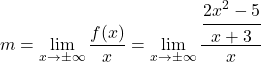
Kita menyederhanakan pecahan dengan menerapkan sifat-sifat pecahan:
![]()
![]()
Dan kami menentukan batasnya:
![]()
Limit tersebut memberikan bilangan real selain nol, sehingga merupakan fungsi rasional dengan asimtot miring yang kemiringannya 2.
Sekarang mari kita hitung intersepnya dengan menerapkan rumus yang sesuai:
![]()
Kami mencoba menghitung batasnya:
![]()
Tapi kita mendapatkan perbedaan ketidakpastian dari ketidakterbatasan. Oleh karena itu, kami mengurangi suku-suku tersebut menjadi penyebut yang sama dan kemudian mengoperasikannya:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle n = \lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-2x\right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-\frac{2x\cdot (x+3)}{x+3} \right] = \\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{2x^2-5}{x+3}-\frac{2x^2+6x}{x+3}\right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty}\frac{2x^2-5-(2x^2+6x)}{x+3}\\[6ex]\displaystyle =\lim_{x \to \pm\infty}\frac{2x^2-5-2x^2-6x}{x+3}=\\[6ex]=\displaystyle \lim_{x \to \pm\infty} \frac{-6x-5}{x+3}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4920e8b21b180c4f2740ce712d9f30d0_l3.png)
Dan akhirnya, kami menyelesaikan batasannya:
![]()
Ringkasnya, asimtot miring dari fungsi pecahan adalah:
![]()
![]()