Aturan atau hukum jajaran genjang

Di halaman ini Anda akan menemukan penjelasan tentang kaidah (atau hukum) jajar genjang. Selain itu, Anda akan melihat beberapa contoh penjumlahan dan pengurangan vektor menggunakan aturan jajaran genjang, serta penerapannya di dunia nyata.

Apa aturan jajaran genjang?

Seperti yang telah anda ketahui, besaran vektor tidak dapat dijumlahkan atau dikurangkan seperti bilangan real, karena mempunyai 2 komponen (di R2) atau 3 komponen (di R3) dan karena vektor dapat mempunyai arah yang berbeda-beda. Oleh karena itu, diperlukan metode lain untuk melakukan operasi vektor, seperti aturan jajar genjang yang terdiri dari sebagai berikut:

Dalam matematika, aturan jajaran genjang adalah prosedur untuk menjumlahkan atau mengurangkan dua vektor dari representasi grafisnya.

Metode jajar genjang tentunya paling banyak digunakan dalam penjumlahan dan pengurangan vektor (secara grafis), karena tekniknya sangat mudah digunakan. Misalnya, dalam fisika digunakan untuk menambah dan mengurangi gaya.

Di sisi lain, aturannya sedikit berbeda tergantung pada apakah kita ingin menjumlahkan atau mengurangi vektor, jadi di bawah ini kami akan menjelaskan kedua versi tersebut secara terpisah.

Aturan jajar genjang untuk menjumlahkan dua vektor

Jika kita ingin menjumlahkan dua vektor secara grafis, langkah-langkah menerapkan aturan atau hukum jajar genjang adalah:

1. Pertama, kita menggambar vektor-vektornya dan menempatkannya pada titik penerapan yang sama, yaitu kita menempatkan asal-usul kedua vektor tersebut pada titik yang sama.
2. Kemudian kita menggambar di ujung salah satu vektor sebuah garis yang sejajar dengan vektor lainnya. Dan kami mengulangi langkah tersebut dengan vektor lainnya. Oleh karena itu, kita akan mendapatkan gambar jajar genjang (sesuai dengan nama aturannya).
3. Terakhir, vektor hasil penjumlahan adalah diagonal jajar genjang yang dimulai dari titik asal vektor-vektor tersebut hingga titik potong kedua garis sejajar tersebut.

Dalam contoh umum berikut, Anda dapat melihat bagaimana aturan jajaran genjang digunakan:

Jika Anda ingin berlatih dengan aturan jajaran genjang, di tautan berikut Anda dapat melihat lebih banyak contoh dan beberapa latihan penjumlahan vektor yang diselesaikan . Di halaman ini Anda juga akan menemukan metode lain untuk menjumlahkan vektor secara grafis dan bahkan cara menjumlahkannya secara numerik.

Aturan jajar genjang untuk mengurangkan dua buah vektor

Aturan atau metode jajaran genjang juga digunakan untuk mengurangkan dua vektor dari suatu grafik. Jadi, langkah-langkah pengurangan vektor adalah:

1. Pertama, kita nyatakan kedua vektor pada grafik dan posisikan keduanya pada titik penerapan yang sama, yaitu kita letakkan titik asal kedua vektor pada titik yang sama.
2. Kedua, kita menggambar vektor yang berlawanan dengan vektor yang dikurangkan pada operasi tersebut, atau dengan kata lain kita membalik vektor yang melakukan pengurangan tersebut.
3. Kemudian kita tarik garis yang sejajar dengan vektor perubahan tanda di ujung vektor yang jumlahnya sama dengan . Dan kami ulangi prosesnya dengan vektor lainnya. Sehingga kita akan mendapatkan gambar jajar genjang (sesuai dengan nama aturannya).
4. Terakhir, hasil pengurangannya adalah vektor yang bergerak dari titik asal kedua vektor tersebut hingga titik perpotongan kedua garis sejajar.

Perhatikan contoh umum berikut dimana dua vektor dikurangkan dengan hukum jajaran genjang:

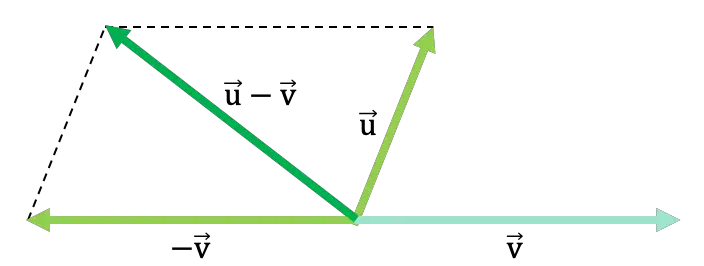
Di tautan berikut Anda dapat melihat lebih banyak contoh pengurangan vektor dengan aturan jajaran genjang, Anda juga dapat berlatih dengan latihan pengurangan vektor yang diselesaikan . Selain itu, Anda akan menemukan teknik lain untuk mengurangkan vektor dari grafiknya dan, terakhir, cara mengurangkannya secara numerik.

Terakhir, jika penjelasan teknik ini bermanfaat bagi Anda, pasti Anda juga tertarik untuk mengetahui apa itu kaidah tangan kanan . Pada halaman tautan Anda dapat melihat apa itu, operasi vektor apa yang digunakan dan berbagai variasi aturan yang ada.