Di halaman ini kami menjelaskan apa itu sistem koordinat dan, sebagai tambahan, Anda akan menemukan segala sesuatu tentang sistem koordinat Cartesian. Anda juga akan melihat jenis sistem koordinat lainnya (kutub, silinder, bola, dll.) dan penerapan sistem koordinat di dunia nyata.
Apa itu sistem koordinat?
Walaupun pada awalnya agak sulit untuk memahami konsep ini, namun pengertian sistem koordinat adalah:
Sistem koordinat adalah sistem yang memungkinkan kita mengidentifikasi posisi suatu titik. Artinya, ini adalah sekumpulan nilai yang digunakan untuk menentukan lokasi objek geometris apa pun.
Misalnya, posisi terbang pesawat berikut dapat digambarkan dengan sistem koordinat:
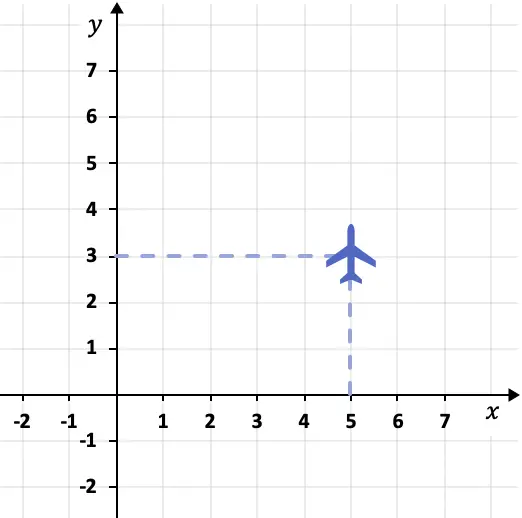
Dalam hal ini, bidang berada di titik (5.3). Karena koordinat X-nya 5 dan koordinat Y-nya 3.
![]()
Sebaliknya titik (0,0) disebut titik asal koordinat , karena merupakan titik awal sumbu koordinat dan merupakan titik acuan sistem koordinat.
Karena penasaran, ahli matematika yang menemukan sistem koordinat dianggap sebagai orang Prancis René Descartes. Oleh karena itu disebut juga sistem koordinat kartesius.
Sistem koordinat kartesius pada bidang
Grafik yang kita lihat pada bagian sebelumnya termasuk dalam sistem koordinat kartesius pada bidang. Kita katakan ia berada pada bidang karena merupakan sistem dua dimensi, artinya ia hanya mempunyai dua sumbu: sumbu X dan sumbu Y.
Sumbu X mewakili koordinat horizontal, sedangkan sumbu Y mewakili koordinat vertikal. Di bawah ini Anda dapat melihat beberapa titik yang direpresentasikan secara grafis beserta koordinatnya:
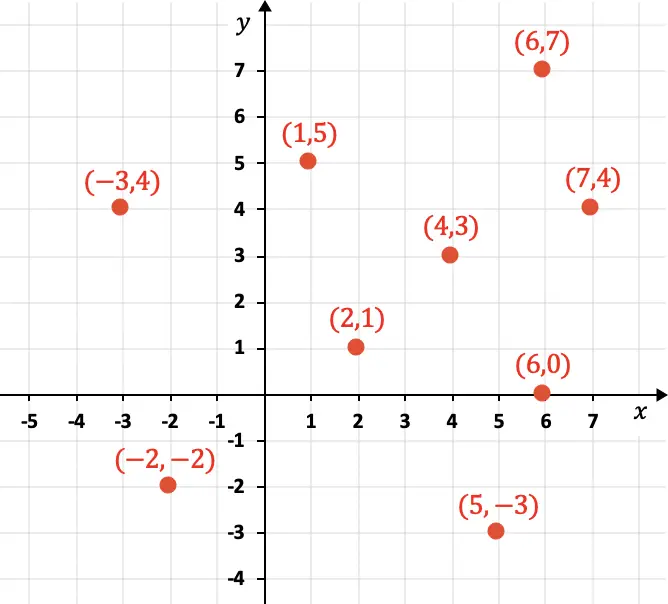
Seperti terlihat pada grafik, koordinat direpresentasikan secara numerik dengan tanda kurung, selain itu komponen X didahulukan baru kemudian komponen Y: (4,3). Selain itu, koordinat bisa positif, negatif, atau nol.
Di sisi lain, sistem koordinat jenis ini disebut juga bidang kartesius.
Terakhir, Anda harus tahu bahwa sumbu koordinat dapat dinyatakan dalam beberapa cara, meskipun semuanya memiliki arti yang sama:
- Sumbu X disebut juga sumbu absis atau sumbu OX.
- Sumbu Y disebut juga sumbu y atau sumbu OY.
Sistem koordinat kartesius di ruang angkasa
Kita baru saja melihat bagaimana merepresentasikan suatu titik pada bidang, yaitu dalam sistem koordinat dengan dua sumbu (2 dimensi). Namun kenyataannya terdiri dari 3 dimensi (tinggi, lebar dan kedalaman).
Jadi, dalam geometri Euclidean, ruang tiga dimensi umumnya diwakili oleh sistem koordinat dengan tiga sumbu, semuanya tegak lurus satu sama lain:
- Sumbu X mewakili kedalaman.
- Sumbu Y menunjukkan lebarnya.
- Sumbu Z berhubungan dengan ketinggian.
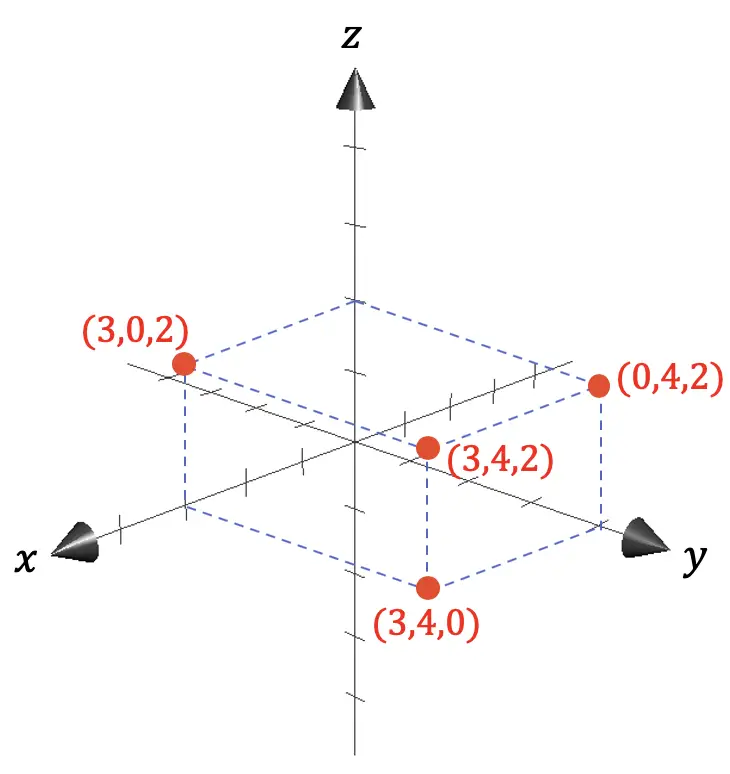
Seperti yang Anda lihat pada representasi grafis sebelumnya, koordinat titik mana pun diberikan oleh proyeksi pada sumbu jarak antara titik tersebut dan titik asal (0,0,0).
sistem koordinat kutub
Sistem koordinat kartesius, 2D atau 3D, adalah yang paling banyak digunakan. Namun pada beberapa kesempatan mungkin lebih mudah bagi kita untuk menggunakan sistem koordinat jenis lain.
Sistem koordinat kutub merupakan sistem acuan dua dimensi yang koordinatnya adalah:
-

adalah jarak antara titik asal koordinat dan titik. Ini disebut koordinat radial.
-

adalah sudut yang dibuat sumbu X dengan garis yang melalui titik dan titik asal. Ini disebut koordinat sudut atau azimut.
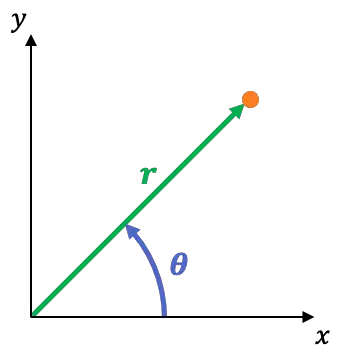
Anda dapat dengan mudah beralih dari sistem koordinat persegi panjang ke sistem koordinat kutub menggunakan persamaan berikut:
Ubah koordinat kutub menjadi koordinat kartesius
![]()
![]()
Peralihan dari koordinat Kartesius ke koordinat kutub
![]()
![]()
Sistem koordinat silinder
Sistem koordinat silinder sangat mirip dengan sistem koordinat kutub. Sebenarnya sama saja tetapi dengan satu koordinat lagi: tinggi.
Oleh karena itu, bingkai silinder adalah bingkai tiga dimensi, yaitu dengan 3 koordinat:
-

adalah proyeksi ortogonal titik pada bidang XY, atau dengan kata lain jarak titik terhadap sumbu Z.
-

adalah sudut sumbu semi positif

-

adalah ketinggian titik, sama dengan koordinat sistem koordinat Kartesius di ruang angkasa.
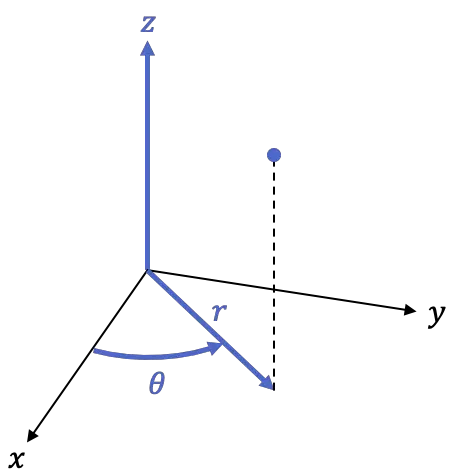
Rumus berikut digunakan untuk mengubah sistem koordinat kartesius menjadi koordinat silinder:
Ubah koordinat silinder menjadi koordinat kartesius
![]()
![]()
![]()
Ubah koordinat kartesius menjadi koordinat silinder
![]()
![]()
![]()
Sistem koordinat bola
Terakhir, kita memiliki sistem koordinat bola. Sistem koordinat jenis ini juga sangat mirip dengan koordinat kutub dan koordinat silinder, meskipun jelas terdapat beberapa perbedaan dari keduanya.
Sistem koordinat bola merupakan suatu sistem untuk menggambarkan ruang Euclidean tiga dimensi, oleh karena itu mempunyai tiga koordinat:
-

adalah jarak (dalam R3) dari titik asal ke titik.
-

adalah sudut yang dibentuk bagian positif sumbu X terhadap garis

diproyeksikan ke bidang XY.
-
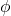
adalah sudut antara bagian positif sumbu Z dan garis

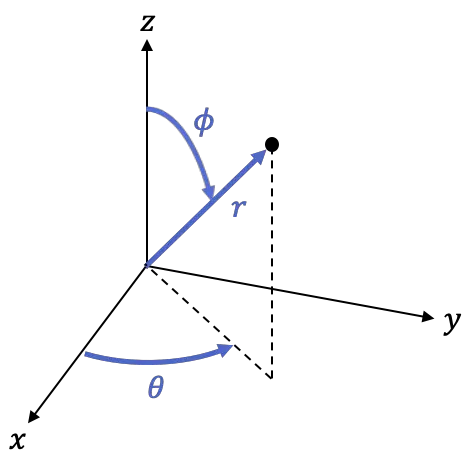
Anda dapat beralih antara koordinat bola dan kartesius menggunakan rumus berikut:
Mengubah koordinat bola menjadi koordinat kartesius
![]()
![]()
![]()
Mengubah koordinat kartesius menjadi koordinat bola
![]()
![]()
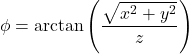
Aplikasi sistem koordinat di dunia nyata
Sistem koordinat sangat penting dalam matematika karena juga digunakan dalam kehidupan nyata. Misalnya, berguna untuk menemukan lokasi objek, orang, atau bahkan tempat di peta. Faktanya, GPS ada karena sistem koordinat, karena itulah yang digunakan untuk mengetahui posisi Anda di Bumi.
Lebih tepatnya, koordinat geografis GPS terdiri dari dua elemen: lintang dan bujur. Lintang (utara atau selatan) dan bujur (timur atau barat) adalah dua koordinat sudut yang mengukur sudut antara pusat bumi dan lokasi Anda. Keduanya dinyatakan dalam derajat, baik dalam koordinat desimal maupun sexagesimal.