Metode kuadrat terkecil adalah alat matematika untuk menemukan garis lurus terbaik yang bersesuaian dengan sekumpulan titik . Kami menjelaskannya kepada Anda dengan cara yang sederhana:
Bayangkan Anda memiliki sekumpulan titik pada grafik yang tersebar di sana-sini. Anda ingin mencari garis lurus yang paling “sesuai” dengan titik-titik tersebut, sehingga dapat memperkecil jarak antara garis dan titik-titik tersebut . Inilah ide dibalik metode kuadrat terkecil.
Metode tersebut menggunakan rumus untuk menghitung persamaan garis yang meminimalkan jumlah kuadrat selisih antara titik dan garis. Artinya, mencari garis yang mempunyai “deviasi” terkecil dari titik-titiknya.
Secara sederhana, metode kuadrat terkecil berguna untuk menganalisis data yang diperoleh selama penyelidikan, dengan tujuan mengekspresikan perilaku mereka secara linier, mengurangi kesalahan informasi yang dicuri.
Siapa yang menciptakan metode kuadrat terkecil?
Metode kuadrat terkecil, alat fundamental dalam statistik dan analisis data, dikaitkan dengan matematikawan Jerman Carl Friedrich Gauss , yang mengusulkannya pada tahun 1794. Namun, Gauss baru mempublikasikannya pada tahun 1809 .
Menariknya, matematikawan Perancis Andrien-Marie Legendre menerbitkan versi serupa pada tahun 1805 , mengembangkannya secara mandiri.
Kedua ahli matematika tersebut membantu menciptakan metode yang telah banyak digunakan di berbagai disiplin ilmu untuk menyesuaikan model dengan data yang diamati dan membuat prediksi yang akurat.
Rumus kuadrat terkecil
Tidak diragukan lagi, untuk memahami apa saja yang tercakup dalam metode ini, penting untuk menjelaskan rumusan dan proses penerapannya. Berikut penjelasan detail mengenai rumus kuadrat terkecil:
mendefinisikan masalahnya
Katakanlah Anda memiliki kumpulan data dengan dua variabel, variabel independen (x) dan variabel dependen (y), dan Anda ingin memasukkan garis lurus ke data ini.
Tujuannya adalah untuk mencari nilai koefisien persamaan garis (titik potong dan kemiringan) yang meminimalkan jumlah kuadrat selisih antara nilai riil y, dan nilai prediksi dari garis yang dipasang.
Hitung persamaan garisnya
Persamaan garis berbentuk y = mx + b, dengan m adalah kemiringan dan b adalah titik potong y. Rumus kuadrat terkecil untuk menghitung nilai myb adalah:
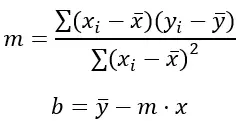
Emas:
Σ mewakili jumlah nilai.
x i dan y i masing-masing merupakan nilai variabel x dan y untuk setiap titik data.
x̄ dan ȳ masing-masing merupakan rata-rata dari nilai x dan y.
( xi – x̄) dan (y i – ȳ) adalah selisih antara nilai x dan y serta meannya masing-masing.
( xi – x̄) 2 adalah kuadrat selisih antara nilai x dan meannya.
menafsirkan hasilnya
Setelah Anda menghitung nilai m dan b menggunakan rumus tersebut, Anda dapat menggunakannya untuk mendapatkan persamaan garis pas. Misalnya, jika Anda memiliki m = 2 dan b = 3, maka persamaan garis yang dipasang adalah y = 2x + 3. Hal ini memungkinkan Anda membuat prediksi atau perkiraan nilai y untuk nilai x yang berbeda berdasarkan hak yang disesuaikan.
Kapan metode kuadrat terkecil digunakan?
Anda mungkin akan bertanya pada diri sendiri, kapan metode ini digunakan? Ini sangat berguna dalam berbagai situasi! Misalnya ketika Anda ingin menganalisis data eksperimen atau penelitian untuk menemukan hubungan atau tren .
Misalkan Anda sedang menyelidiki hubungan antara harga sebuah rumah dan ukurannya dalam meter persegi. Anda dapat menggunakan metode kuadrat terkecil untuk menemukan garis lurus yang paling sesuai dengan data dan memberi Anda gambaran yang jelas tentang hubungan ini.
Ini juga digunakan dalam ilmu ekonomi untuk memodelkan dan memprediksi variabel seperti permintaan produk atau perilaku harga . Selain itu, dalam bidang teknik, metode kuadrat terkecil diterapkan untuk menyesuaikan model matematika dengan data pengujian atau simulasi.
Metode kuadrat terkecil adalah alat yang ampuh dan serbaguna yang digunakan di banyak bidang studi dan pekerjaan untuk menganalisis data dan menemukan hubungan penting.
Penerapan metode kuadrat terkecil pada teorema lain
Selain penggunaannya sendiri, metode kuadrat terkecil sangat berguna dalam teorema lain. Mari kita lihat lebih banyak tentang subjek ini di bawah.
Teorema regresi
Ini banyak digunakan dalam teorema regresi untuk menemukan garis terbaik yang sesuai dengan sekumpulan data . Misalnya, Anda dapat menggunakannya untuk menganalisis hubungan antara tinggi tanaman dan jumlah cahaya yang diterimanya untuk menentukan bagaimana tanaman akan tumbuh dalam kondisi pencahayaan berbeda.
Interpolasi teorema
Dalam hal ini, metode kuadrat terkecil juga diterapkan pada teorema interpolasi untuk mencari fungsi polinomial yang paling sesuai dengan sekumpulan titik. Misalnya, Anda dapat menggunakannya untuk memperkirakan lintasan suatu benda bergerak berdasarkan data posisi dan waktu.
Teorema kesesuaian kurva
Ini digunakan dalam teorema pemasangan kurva untuk menemukan kurva yang sesuai dengan sekumpulan data . Hal ini berguna dalam aplikasi seperti pemodelan data iklim untuk memprediksi perubahan iklim atau memprediksi lintasan proyektil.
Teorema analisis Fourier
Dalam teorema analisis Fourier, metode kuadrat terkecil digunakan untuk memperkirakan fungsi periodik dari serangkaian data diskrit . Ini berlaku untuk pensinyalan data dan kompresi gambar dan suara.
Teorema Regresi Nonlinier
Terakhir, metode kuadrat terkecil juga diterapkan dalam teorema regresi nonlinier untuk mencari kurva terbaik yang sesuai dengan kumpulan data yang tidak mengikuti hubungan linier . Misalnya, Anda dapat menggunakannya untuk menganalisis bagaimana konsentrasi suatu bahan kimia mempengaruhi laju reaksi.
Contoh metode kuadrat terkecil
Untuk lebih memahami bagaimana Anda dapat menerapkan metode kuadrat terkecil, mari kita lihat contoh di bawah ini.
Misalkan Anda memiliki data tinggi tanaman berikut (dalam sentimeter) pada minggu yang berbeda:
| Pekan | tinggi dalam sentimeter |
| 1 | sepuluh |
| 2 | 12 |
| 3 | 14 |
| 4 | 16 |
| 5 | 18 |
| 6 | dua puluh |
Anda ingin menemukan garis lurus terbaik yang sesuai dengan data ini untuk membuat prediksi tinggi tanaman di masa depan.
Langkah 1 : Buat grafik datanya
Hal pertama yang harus dilakukan adalah memplot data pada plot sebar. Sumbu x mewakili minggu dan sumbu y mewakili tinggi badan dalam sentimeter. Berikut grafiknya:
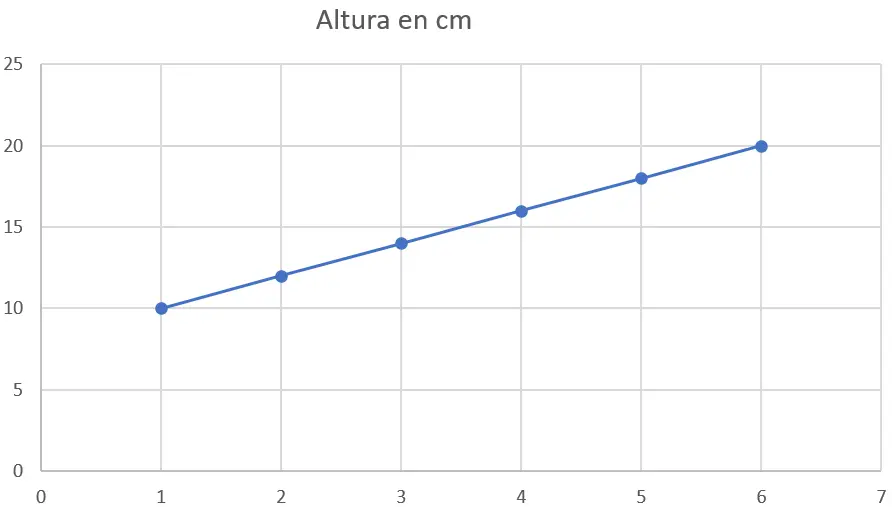
Langkah 2 : Terapkan metode kuadrat terkecil
Metode kuadrat terkecil berupaya mencari garis yang meminimalkan jumlah kuadrat selisih antara data aktual dan nilai prediksi garis tersebut. Dalam hal ini, garis dinyatakan dengan persamaan garis: y = mx + b, dimana “y” adalah tinggi, “x” adalah minggu, “m” adalah kemiringan garis dan “b” adalah perpotongan y.
Untuk mencari nilai “m” dan “b” yang meminimalkan jumlah kuadrat selisihnya, digunakan rumus sebagai berikut:
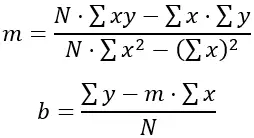
Dimana N adalah jumlah titik data (dalam hal ini, 6), Σxy adalah jumlah minggu dikalikan tinggi badan, Σx adalah jumlah minggu, Σy adalah jumlah tinggi badan, dan Σx 2 adalah jumlah kuadrat minggu .
Menerapkan rumus ini pada data tinggi badan, kita memperoleh:
Σxy = 1 10 + 2 12 + 3 14 + 4 16 + 5 18 + 6 20 = 630
Σx = 1 + 2 + 3 + 4 + 5 + 6 = 21
Σy = 10 + 12 + 14 + 16 + 18 + 20 = 90
Σx 2 = 1 2 + 2 2 + 3 2 + 4 2 + 5 2 + 6 2 = 91
Substitusikan nilai-nilai ini ke dalam rumus “m” dan “b”:
m = (6 · 630 – 21 · 90) − (6 · 91 – 21 2 ) ≈ 2,07
b = (90 – 2,07 · 21) − 6 ≈ 3,24
Oleh karena itu, persamaan garis lurus yang sesuai dengan data ketinggian adalah: y.