Regresi linier adalah metode statistik yang digunakan untuk mempelajari hubungan antara dua variabel kontinu . Ide utama dari regresi linier adalah menemukan garis lurus yang paling sesuai dengan data. Selain itu, ini memungkinkan Anda memprediksi nilai satu variabel berdasarkan nilai variabel lainnya.
Garis lurus ini disebut “regresi” dan digunakan untuk memprediksi nilai yang tidak diketahui atau untuk memahami hubungan antar variabel. Singkatnya, regresi linier adalah alat untuk menganalisis dan memodelkan hubungan antara dua variabel kontinu.
Mengapa regresi linier penting?
Regresi linier penting karena memungkinkan Anda memodelkan dan menganalisis hubungan antara dua variabel kontinu , yang berguna untuk memprediksi nilai masa depan dan mengidentifikasi pola dan tren data.
Selain itu, regresi linier adalah alat mendasar dalam statistik dan sebagian besar bidang penelitian ilmiah dan sosial, termasuk ekonomi, psikologi, kedokteran, teknik, dan fisika. Ini juga digunakan dalam pengambilan keputusan bisnis dan optimalisasi proses di industri dan bisnis.
Singkatnya, regresi linier adalah alat yang ampuh dan serbaguna yang memungkinkan analisis dan pemahaman yang lebih baik tentang data dan hubungan antar variabel di berbagai bidang penelitian dan praktik.
Apa saja jenis-jenis regresi linier?
Ada beberapa jenis regresi linier, beberapa di antaranya adalah:
regresi linier sederhana
Analisis regresi linier sederhana merupakan alat yang banyak digunakan untuk mempelajari pengaruh suatu variabel bebas terhadap satu variabel terikat , yang dianggap terdapat hubungan linier di antara keduanya. Persamaan regresi linier sederhana memungkinkan kita memperkirakan nilai variabel terikat berdasarkan nilai variabel bebas.
Rumus regresi linier sederhana adalah:
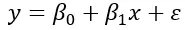
Dimana, β 0 merupakan nilai variabel terikat ketika variabel bebas bernilai nol. β 1 mewakili perubahan variabel terikat per satuan perubahan variabel bebas dan ε mewakili sisa atau kesalahan. Artinya, variabilitas data yang tidak dapat dijelaskan oleh hubungan linier rumusnya.
Regresi linier berganda
Regresi linier berganda digunakan apabila terdapat lebih dari satu variabel bebas yang dapat mempengaruhi variabel terikat yang diteliti.
Rumus regresi linier berganda adalah:
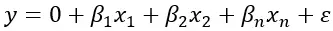
Dimana Y mewakili variabel terikat , β 1 , β 2 , β n merupakan variabel bebas yang dapat mempengaruhi nilai Y, regresi dan ε mewakili kemungkinan kesalahan yang ada. Rumus ini memungkinkan kita memperkirakan nilai Y berdasarkan nilai variabel independen.
Apa rumus regresi linier?
Rumus regresi liniernya adalah:
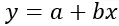
Emas:
y adalah variabel terikat (atau respon) yang akan diprediksi
x adalah variabel independen (atau prediktor) yang digunakan untuk membuat prediksi
a adalah titik potong (atau titik perpotongan garis regresi dengan sumbu Y ketika x=0)
b adalah kemiringan garis regresi (menunjukkan laju perubahan y untuk setiap perubahan x)
Untuk mencari nilai a dan b, kita menggunakan metode kuadrat terkecil yang berupaya meminimalkan jumlah kesalahan kuadrat antara nilai yang diamati dan nilai yang diprediksi oleh garis regresi.
Berikut rumusnya:
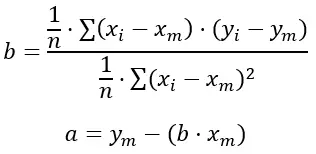
Emas:
n adalah jumlah total dataset yang kita miliki.
x i dan y i adalah nilai yang kita ambil dalam penjumlahannya.
x m dan y m adalah nilai rata-rata dari masing-masing variabel.
Bagaimana cara menerapkan metode regresi linier?
Metode regresi linier dapat diterapkan dengan mengikuti langkah-langkah di bawah ini:
- Kumpulkan data : Hal pertama yang harus dilakukan adalah mengumpulkan data yang Anda minati. Misalnya, jika Anda ingin mempelajari hubungan antara gaji dan usia sekelompok orang, Anda perlu mengumpulkan informasi tentang gaji dan usia masing-masing orang.
- Plot data – Selanjutnya, Anda perlu memplot data pada bidang Kartesius, di mana variabel independen (dalam hal ini usia) ditempatkan pada sumbu horizontal dan variabel dependen (gaji) ditempatkan pada sumbu vertikal.
- Tentukan garis regresi : Garis regresi yang paling sesuai dengan data harus ditentukan. Garis ini diperoleh dari rumus regresi linier yang dihitung menggunakan data statistik sampel .
- Menilai Kesesuaian – Penting untuk menilai seberapa cocok garis regresi dengan data. Hal ini dapat dilakukan dengan menggunakan pengukuran statistik.
- Buat prediksi – Terakhir, prediksi dapat dibuat menggunakan garis regresi yang dihasilkan. Misalnya, jika Anda ingin memprediksi gaji seseorang berusia 30 tahun, Anda akan menggunakan rumus regresi linier dan mengganti nilai usia ke dalamnya.
Penting untuk diperhatikan bahwa langkah-langkah ini mungkin sedikit berbeda tergantung pada jenis regresi linier yang digunakan dan perangkat lunak statistik yang digunakan.
Untuk apa regresi linier digunakan?
Regresi linier digunakan ketika ingin menganalisis hubungan antara dua variabel , dimana variabel yang satu dapat mempengaruhi nilai variabel lainnya. Oleh karena itu, regresi linier dapat digunakan untuk memahami bagaimana suatu variabel independen mempengaruhi variabel dependen dan untuk memprediksi nilai variabel dependen berdasarkan variabel independen.
Perlu diperhatikan bahwa regresi linier mengasumsikan hubungan kedua variabel bersifat linier , artinya perubahan variabel terikat sebanding dengan perubahan variabel bebas.
Oleh karena itu, regresi linier sebaiknya digunakan bila diduga ada hubungan linier antara kedua variabel. Jika kondisi ini tidak terpenuhi, mungkin lebih tepat menggunakan model regresi nonlinier lain atau metode statistik yang berbeda.
Apa saja penerapan regresi linier?
Regresi linier digunakan dalam berbagai aplikasi di berbagai bidang seperti statistik, ekonomi, teknik, ilmu sosial, biologi, dan lain-lain. Berikut beberapa penerapan regresi linier yang paling umum:
- Analisis Tren – Untuk menganalisis tren dalam data historis dan memprediksi tren masa depan.
- Peramalan – Memprediksi nilai masa depan suatu variabel berdasarkan nilai masa lalu dari satu atau lebih variabel.
- Riset pasar : studi tentang hubungan antara permintaan suatu produk dan harganya.
- Analisis Keuangan – Mempelajari hubungan antara pendapatan dan pengeluaran perusahaan dan memperkirakan hasil keuangan di masa depan.
- Studi epidemiologi : mempelajari hubungan antara paparan faktor risiko dan kemungkinan berkembangnya suatu penyakit.
- Ilmu Sosial – Mempelajari hubungan antara dua variabel atau lebih dalam bidang seperti psikologi, sosiologi, dan ilmu politik.
- Riset Operasi – Regresi linier digunakan untuk memodelkan dan mengoptimalkan sistem yang kompleks di berbagai bidang seperti teknik industri dan logistik.
- Ilmu Lingkungan – Digunakan untuk mempelajari hubungan antara faktor lingkungan dan pengaruhnya terhadap ekosistem.
Apa yang dimaksud dengan residu dalam regresi linier?
Residual dalam regresi linier adalah selisih antara nilai observasi variabel terikat dengan nilai yang diprediksi oleh model regresi linier . Dengan kata lain, ini adalah jarak vertikal antara titik data aktual dan garis regresi.
Ide di balik residu adalah jika garis regresi cocok dengan data, maka residunya harus kecil dan acak. Jika residunya besar atau mengikuti pola tertentu, hal ini mungkin merupakan tanda bahwa hubungan antar variabel tidak linier atau model regresi linier tidak sesuai dengan data.
Residual juga digunakan untuk mengevaluasi keakuratan model regresi linier dan untuk mengidentifikasi outlier atau titik data berpengaruh yang dapat mempengaruhi kualitas model.
Bisakah saya menjalankan regresi linier dengan lebih dari satu variabel terikat?
Dalam regresi linier, variabel terikat selalu berupa variabel tunggal. Namun, Anda dapat memiliki lebih dari satu variabel independen. Dalam hal ini, kita akan berbicara tentang regresi linier berganda .
Dalam regresi linier berganda, tujuannya adalah untuk mempelajari pengaruh beberapa variabel independen terhadap satu variabel dependen.
Bagaimana cara menafsirkan koefisien dalam regresi linier?
Dalam regresi linier, koefisien mewakili kemiringan dan titik potong garis regresi . Kemiringan menunjukkan perubahan variabel terikat per satuan perubahan variabel bebas, sedangkan titik potong menyatakan nilai variabel terikat ketika variabel bebas sama dengan nol.
Contoh Numerik Regresi Linier
Contoh sederhananya mungkin sebagai berikut:
Misalkan kita memiliki data usia dan tinggi badan berikut untuk sekelompok orang:
| usia tahun) | tinggi (cm) |
| 25 | 170 |
| 30 | 175 |
| 35 | 180 |
| 40 | 185 |
| Empat lima | 190 |
Kami ingin mengetahui apakah ada hubungan antara usia dan tinggi badan orang-orang ini. Untuk melakukan ini, kita akan menggunakan regresi linier.
Pertama, kita dapat menggambar grafik statistik dengan datanya (dalam hal ini kami menyarankan menggunakan plot sebar):
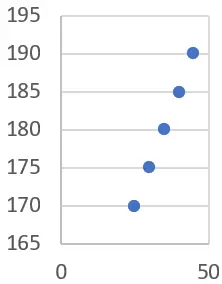
Kita dapat melihat bahwa ada kecenderungan yang jelas bahwa seiring bertambahnya usia, tinggi badan juga meningkat. Hal ini dapat kita pastikan dengan menghitung garis regresi linier.
Dengan menghitung koefisien garis regresi linier dengan rumus yang telah kita lihat sebelumnya, diperoleh:
pada = 145
b = 1
Oleh karena itu, persamaan garis regresi liniernya adalah:
Tinggi Badan = 145 + 1 Umur
Kita bisa menggunakan persamaan ini untuk memprediksi tinggi badan seseorang berdasarkan usianya. Misalnya, jika seseorang berumur 32 tahun, kita dapat memperkirakan tinggi badannya adalah:
Tinggi = 145 + 1 32 = 177 cm