Bilangan Euler (juga dikenal sebagai konstanta Euler) adalah bilangan matematika yang penting dan esensial dalam berbagai bidang matematika, termasuk teori bilangan, topologi, teori grup, dan teori fungsi. Dilambangkan dengan huruf Yunani “e” dan nilai perkiraannya adalah 2,71828.
Bilangan e mengikuti rumus fungsi eksponensial dan merupakan bilangan dasar dalam teori bilangan kompleks.
Ini juga merupakan bilangan asli yang muncul dalam menyelesaikan banyak masalah matematika, termasuk menghitung probabilitas dan memodelkan proses pertumbuhan dan peluruhan.
Apa asal usul bilangan Euler?
Nama bilangan Euler diambil dari nama ahli matematika Swiss Leonhard Euler (1707-1783), yang merupakan salah satu ahli matematika terhebat sepanjang masa dan dianggap sebagai bapak matematika modern.
Euler memberikan kontribusi berharga pada banyak bidang matematika, termasuk teori bilangan, geometri, kalkulus, fisika, dan astronomi.
Dialah yang pertama kali mendefinisikan dan menggunakan bilangan e (disebut bilangan Euler) dalam karyanya tentang perhitungan dan teori logaritma. Rumus Euler untuk bilangan kompleks juga merupakan salah satu kontribusinya yang paling menonjol pada matematika.
Bagaimana nilai ini diperoleh?
Sebenarnya ada beberapa metode untuk menghitung bilangan Euler. Namun, perlu disebutkan bahwa tidak ada metode yang memberikan hasil pasti. Oleh karena itu, penomorannya bersifat kontinu dan tidak terbatas, tetapi tidak berulang.
Faktanya, saat ini diketahui lebih dari 1 triliun angka yang membentuk angka e. Deret tak hingga yang mendefinisikan bilangan Euler adalah:

Emas “!” adalah faktorial, yang didefinisikan sebagai hasil kali semua bilangan asli sampai bilangan tersebut. Misalnya:
5! = 5 4 3 2 1 = 120
Kita dapat melihat deret ini secara grafis sebagai jumlah deret persegi panjang yang tingginya 1 dan lebarnya diperkecil, dengan lebar setiap persegi panjang adalah 1/n!, dengan n adalah banyaknya faktorial.
Jika kita menambah jumlah persegi panjang, perkiraan luas di bawah kurva fungsi eksponensial semakin mendekati bilangan Euler.
Ringkasnya, bilangan Euler adalah bilangan yang dihasilkan dari penjumlahan deret tak hingga dan merupakan dasar dalam banyak bidang matematika. Meskipun merupakan bilangan irasional , nilai perkiraannya adalah 2,71828.
Penting untuk diingat bahwa Euler sendiri menerapkan metode ini untuk menghitung e hingga 18 tempat desimal.
Cara lain untuk menghitungnya:
Kita dapat menghitung perkiraan nilai bilangan Euler pada suatu garis menggunakan serangkaian suku berhingga . Misalnya, jika kita mengambil deret tak hingga pertama yang didefinisikan di atas:

Kita dapat menghitung nilai perkiraannya dengan menjumlahkan suku-suku pertama deret tersebut. Misalnya, jika kita menambahkan 6 suku pertama:
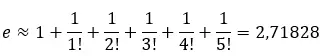
Kita dapat memplot deret ini pada sebuah garis untuk melihat bagaimana deret tersebut mendekati nilai perkiraan 2,71828 .
Secara grafis, garis yang mewakili bilangan Euler dapat digambarkan sebagai rangkaian persegi panjang yang tingginya 1 dan lebarnya diperkecil, dengan lebar setiap persegi panjang adalah 1/n!, dengan n adalah banyaknya faktorial.
Jika kita menambah jumlah persegi panjang, perkiraan luas di bawah kurva fungsi eksponensial semakin mendekati bilangan Euler.
Persamaan eksponensial dengan bilangan Euler
Persamaan eksponensial dengan bilangan Euler dapat digunakan untuk memodelkan berbagai macam fenomena dalam sains seperti fisika, biologi, ekonomi, dan lain-lain. Berikut beberapa contohnya:
Pertumbuhan dan pembusukan yang eksponensial
Model ini menggambarkan laju pertumbuhan atau penurunan populasi, atau laju penguraian zat beracun.
Misalnya, jika suatu populasi tumbuh dengan laju 5% per tahun, maka besarnya populasi dapat dijelaskan dengan rumus:
P(t) = P0 · e 0,05t , dimana P0 adalah jumlah populasi awal.
Model peluruhan radioaktif
Model ini menggambarkan laju peluruhan atom radioaktif seiring waktu.
Rumusnya adalah sebagai berikut:
N(t) = N0 e -λt
dimana N0 adalah jumlah atom awal, λ adalah konstanta yang bergantung pada bahan radioaktif dan t adalah waktu.
Ini hanyalah beberapa contoh bagaimana persamaan eksponensial dengan bilangan Euler dapat digunakan dalam praktik. Ada banyak bidang lain di mana persamaan eksponensial berguna dan relevan.
Apa penerapan bilangan Euler?
Bilangan Euler memiliki penerapan yang luas di berbagai bidang matematika dan sains. Beberapa bidang yang menggunakan angka e adalah:
- Perhitungan dan analisis matematis : digunakan dalam studi fungsi eksponensial dan logaritma, dan dalam penyelesaian persamaan diferensial.
- Teori bilangan – digunakan dalam studi distribusi bilangan prima dan dalam memecahkan masalah yang berkaitan dengan teori bilangan.
- Probabilitas dan Statistik : Digunakan dalam memecahkan masalah yang berkaitan dengan distribusi probabilitas dan memperkirakan nilai yang diharapkan.
- Kriptografi – Digunakan dalam studi algoritma enkripsi dan dekripsi.
- Fisika – digunakan untuk memecahkan masalah yang berkaitan dengan termodinamika, mekanika kuantum, dan fisika statistik.
- Kimia : digunakan dalam memecahkan masalah yang berkaitan dengan termodinamika kimia dan kinetika kimia.
Rumus Euler untuk bilangan kompleks
Rumus Euler untuk bilangan kompleks menetapkan hubungan antara fungsi trigonometri dan eksponensial. Rumusnya tertulis:

Dimana “e” adalah basis logaritma natural, “i” adalah satuan imajiner, “x” adalah bilangan real, dan “cos” dan “sin” masing-masing adalah fungsi trigonometri kosinus dan sinus.
Rumus ini sangat berguna dalam banyak bidang matematika, termasuk teori bilangan, teori fungsi, dan teori kompleksitas, serta memiliki beragam penerapan dalam bidang teknik, fisika, dan ekonomi.
Contoh praktis penggunaannya adalah dalam representasi sinyal dan sistem dalam analisis Fourier, di mana sinyal periodik direpresentasikan sebagai jumlah sinyal sinusoidal kompleks.
Rumus Euler digunakan untuk menggambarkan bagaimana sinyal kompleks ini berhubungan dengan fungsi trigonometri sebenarnya yang menggambarkan sinyal sinusoidal individu.
Bilangan Euler dan bunga majemuk
Bunga majemuk adalah konsep keuangan yang menggambarkan proses dimana sejumlah uang, yang disebut pokok, menghasilkan bunga atas bunga yang meningkat seiring waktu.
Dengan kata lain, bunga yang diperoleh dari suatu investasi tidak hanya berasal dari modal awal, tetapi juga dari bunga yang diperoleh pada periode-periode sebelumnya.
Bilangan Euler dan bunga majemuk saling berkaitan karena rumus menghitung bunga majemuk menggunakan bilangan Euler. Rumus bunga majemuk adalah:
A = P e rt
Dimana A adalah jumlah akhir, P adalah pokok, r adalah tingkat bunga, t adalah waktu dan e adalah bilangan Euler. Dengan cara ini, bilangan Euler merupakan faktor penting dalam rumusan matematika untuk menghitung bunga majemuk.
Contoh penghitungan bunga majemuk dengan angka konkrit adalah:
Asumsikan kita memiliki investasi sebesar €1.000 dengan tingkat bunga 5% per tahun selama 2 tahun. Rumus untuk menghitung bunga majemuk adalah:
A = P e rt = 1000 e 0,05 2 = 1000 1,1025 = €1102,5.
Ini berarti bahwa setelah 2 tahun, modal awal kami sebesar €1.000 akan meningkat menjadi €1.102,5 berkat bunga majemuk yang dihasilkan.
Contoh latihan matematika dengan bilangan Euler
Berikut dua contoh penyelesaian soal matematika yang melibatkan bilangan Euler:
1. Tentukan nilai “e ix ” dimana x adalah bilangan real:
Identitas Euler menyatakan bahwa e ix = cos(x) + i · sin(x). Oleh karena itu, jika kita mengetahui nilai x, kita dapat menghitung nilai e ix menggunakan fungsi trigonometri.
2. Hitung e^(x 2 ) untuk nilai x tertentu:
Kita dapat menggunakan deret Taylor untuk menghitung nilai e^(x 2 ). Deret Taylor e x adalah perluasan tak terhingga yang memungkinkan penghitungan perkiraan nilai e x yang berurutan, bergantung pada suku yang digunakan.

Jika kita mengganti x 2 dengan x pada deret ini, kita memperoleh deret Taylor untuk e^(x 2 ).