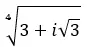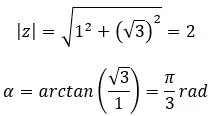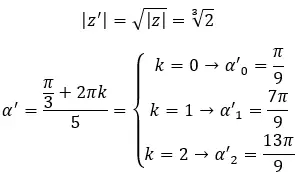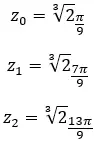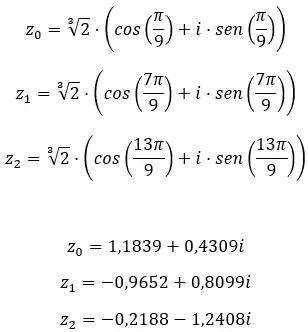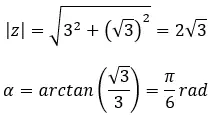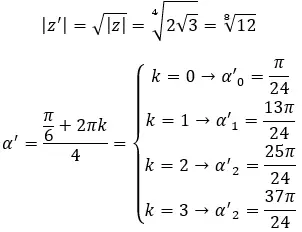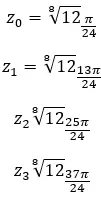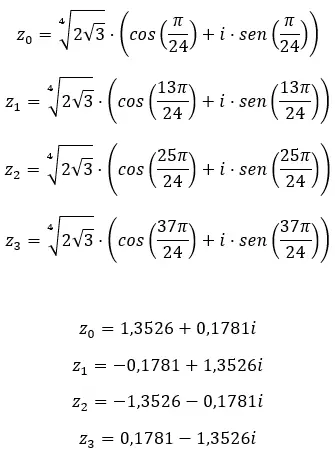Menghitung akar bilangan kompleks cukup sederhana. Nah, setelah Anda memahami prosedurnya, itu cukup berulang. Selanjutnya akan kami jelaskan dan kami berikan contohnya, sehingga Anda dapat mempelajari cara menerapkannya dalam latihan nyata.
akar ke-n bilangan kompleks
Konsep akar ke-n setara dengan akar orde n, oleh karena itu, metode yang sama digunakan untuk menghitung akar kuadrat dan akar kelima suatu bilangan kompleks. Tentu saja, jumlah solusi akan berubah bergantung pada urutan ini.
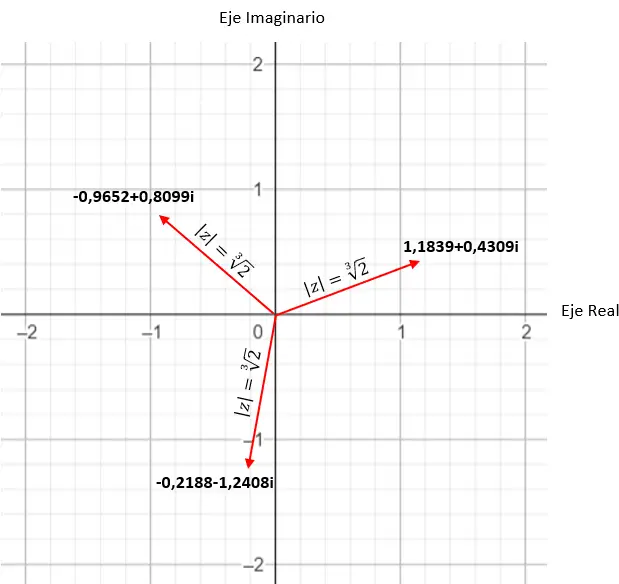
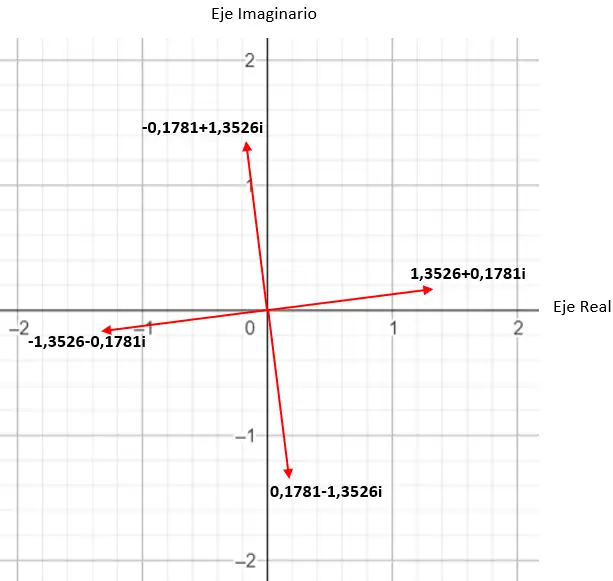
Misalnya, jika kita menghitung akar keempat suatu kompleks, kita memperoleh 4 solusi berbeda. Dan jika kita nyatakan dalam bidang kompleks , kita melihat bahwa terbentuk poligon beraturan dengan 4 sisi, berpusat pada titik asal bidang. Ini adalah properti yang sangat menarik, yang akan kita lihat secara detail nanti (di bagian contoh).
Sekarang setelah kita memperjelas konsep ini, kita akan melihat cara menghitung akar bilangan kompleks dalam bentuk polar (menggunakan notasi ini adalah cara yang paling nyaman untuk menyelesaikan akar.). Sederhananya, Anda perlu menghitung akar modulus dan menyatakan argumennya dalam bentuk n. Dengan kata lain, akar bilangan kompleks berikut (z):
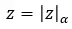
Jumlah ini untuk dihitung:
- Modul: Akar ke-n dari modul awal.
- Argumen: Tambahkan 2πk dalam radian atau 360k dalam derajat ke argumen, dan bagi dengan n.
Secara matematis, untuk menghitung modul dan argumen kita menggunakan dua rumus berikut:
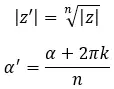
Dimana, k = 0, 1, 2,…, n-1.
Oleh karena itu, kami nyatakan hasilnya sebagai berikut:
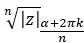
Jelasnya, n solusi yang diperoleh dengan menyelesaikan akar ini akan dibentuk oleh modul yang sama dan n argumen berbeda.
Contoh penghitungan akar kompleks ke-n
Sekarang kita akan melihat beberapa contoh penghitungan akar ke-n bilangan kompleks. Kami menyarankan Anda mencoba menyelesaikannya sendiri dan setelah selesai, lihat perbaikannya. Jangan lupa caranya sudah dijelaskan di atas.
Temukan akar ketiga bilangan kompleks: 1 + i √3 .
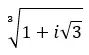
Temukan akar keempat bilangan kompleks: 3+i √ 3 .