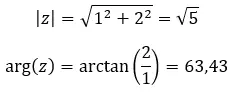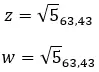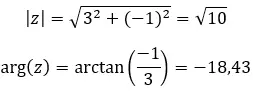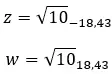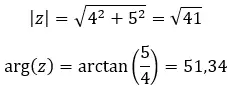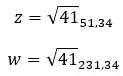Pada artikel ini, kita akan membahas sifat-sifat bilangan kompleks , yang dapat berguna saat menyelesaikan perhitungan dan menyederhanakan ekspresi. Mari langsung ke properti ini.
Modulus dan argumen bilangan kompleks
Sifat pertama bilangan kompleks adalah modulus dan argumen bilangan kompleks. Cara menghitungnya sangat mudah, karena Anda hanya perlu menerapkan beberapa rumus.
Rumus untuk menghitung modul:

Rumus untuk menghitung argumen:

Nah, jika bilangan tersebut dinyatakan dalam bentuk polar atau trigonometri, tidak perlu melakukan perhitungan apa pun. Karena, dalam ekspresi yang sama, modul dan argumen dicantumkan.
Pada gambar di bawah ini Anda dapat melihat rumus bilangan dalam bentuk polar, dimana |z| adalah modulusnya dan α adalah argumennya.

Dan pada gambar lainnya ini Anda dapat melihat struktur suatu bilangan yang dinyatakan dalam bentuk trigonometri, dimana |z| adalah modulusnya dan α adalah argumennya.

bilangan kompleks yang sama
Bilangan kompleks yang sama adalah bilangan yang berbagi modulus dan argumen. Jadi, dari dua nilai ini:

Hal ini sama jika sifat berikut terpenuhi.
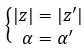
Di sisi lain, jika kita memiliki kedua bilangan dalam bentuk binomial, kita dapat melakukan pemeriksaan dengan cepat dan mudah untuk melihat apakah keduanya merupakan bilangan kompleks yang sama. Sederhananya, ungkapan berikut harus dipenuhi:
a + bi = a + bi
Mari kita lihat contohnya, tentukan apakah dua bilangan kompleks berikut sama:
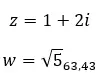
Konjugasi bilangan kompleks
Sekarang mari kita beralih ke salah satu sifat terpenting bilangan kompleks, karena mengetahui cara menghitung konjugasi suatu kompleks sangat membantu kita dalam menyelesaikan pembagian kompleks dan melakukan penyederhanaan.
Jadi, dari dua nilai ini:

Kami mengatakan bahwa mereka terkonjugasi jika mereka berbagi modul dan memiliki argumen yang berlawanan. Oleh karena itu, hal ini harus diselesaikan:
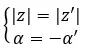
Di sisi lain, jika kita memiliki kedua bilangan dalam bentuk binomial, kita dapat melakukan pemeriksaan dengan cepat dan mudah untuk melihat apakah keduanya merupakan dua bilangan konjugasi kompleks. Sederhananya, ungkapan berikut harus dipenuhi:
un + bi = un – bi
Mari kita lihat contohnya, tentukan apakah dua bilangan kompleks berikut terkonjugasi:
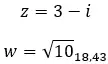
Berlawanan dengan bilangan kompleks
Selanjutnya, kita beralih melihat sifat-sifat bilangan kompleks yang berlawanan. Dari dua nilai ini:

Kita dapat mengatakan bahwa keduanya berlawanan jika mereka mempunyai modulus yang sama dan argumennya berbeda 180 derajat atau π radian:
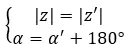
Di sisi lain, jika kita memiliki kedua bilangan dalam bentuk binomial, kita dapat menggunakan metode lain yang lebih cepat dan sederhana untuk mengetahui apakah keduanya merupakan bilangan kompleks yang berlawanan. Sederhananya, ungkapan berikut harus dipenuhi:
a + dua = -a – dua
Mari kita lihat contohnya, tentukan apakah dua bilangan kompleks berikut berlawanan:
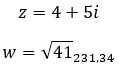
properti lainnya
Tentunya himpunan bilangan ini memiliki sifat lain, seperti bilangan kompleks invers dan beberapa sifat lain yang berhubungan langsung dengan operasi aritmatika dasar. Meskipun semua ini tercakup dalam artikel lain, yang dapat Anda lihat pada daftar di bawah.