Rumus Euler merupakan konsep matematika yang menghubungkan dua konsep dasar matematika: bilangan kompleks dan trigonometri. Hal ini menjadikannya salah satu konseptualisasi yang paling penting dan paling banyak diterapkan dalam semua matematika. Sepanjang artikel ini kita akan melihat seperti apa rumus ini dan semua kegunaannya.
Apa rumus Euler?
Rumus Euler adalah persamaan matematika dasar berdasarkan bilangan Euler , yang menghubungkan bilangan kompleks dengan trigonometri. Ia ditemukan oleh ahli matematika Swiss Leonhard Euler pada abad ke-18 dan sejak itu telah digunakan di berbagai bidang, mulai dari fisika hingga ilmu komputer.
Rumus Euler ditulis sebagai e ix = cos(x) + i sin(x) , dengan e adalah basis logaritma natural, i adalah satuan imajiner (didefinisikan sebagai akar kuadrat dari -1), dan x adalah bilangan real nomor. Persamaan ini menetapkan bahwa bilangan kompleks e ix sama dengan jumlah bilangan real cos(x) dan hasil kali bilangan imajiner i dengan bilangan real sin(x).

Pentingnya rumus Euler terletak pada kenyataan bahwa rumus ini memungkinkan bilangan kompleks dinyatakan dalam bilangan real dan trigonometri, sehingga lebih mudah untuk dimanipulasi dan dihitung.
Bukti rumus Euler
Pembuktian rumus Euler didasarkan pada penggunaan deret Taylor untuk fungsi eksponensial dan identitas trigonometri untuk kosinus dan sinus.
Pertama, kita perhatikan deret Taylor untuk fungsi eksponensial:

Selanjutnya, kita ganti x dengan ix pada persamaan di atas, dimana i adalah satuan imajiner (akar kuadrat dari -1):
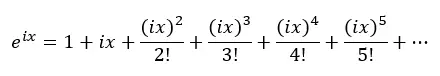
Jadi, kita terapkan pangkat i dan substitusikan ke persamaan sebelumnya:
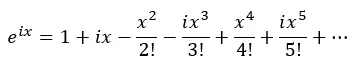
Sekarang kita kelompokkan suku sebenarnya dan suku dengan i:
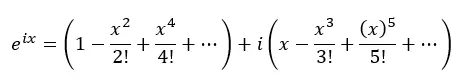
Faktanya, masing-masing tanda kurung di atas adalah deret Taylor untuk kosinus dan sinus:
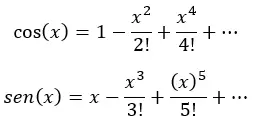
Akhirnya, kita sederhanakan (dengan mengganti setiap ekspresi dalam tanda kurung dengan cosinus dan sinus dari x) dan kita memperoleh:

Contoh rumus Euler
Sekarang setelah Anda mengetahui cara kerja rumus matematika ini, kami sarankan untuk mencoba menyelesaikan contoh praktis berikut: Nyatakan bilangan kompleks e 2i (dalam radian) dalam bentuk binomial:
Penerapan utama rumus Euler adalah mengubah bilangan kompleks yang dinyatakan dalam bentuk eksponensial menjadi bentuk binomial. Oleh karena itu kita akan menggunakan rumus : e ix = cos(x) + i sin(x)
e 2i = cos(2) + saya dosa(2)
e2i = -0,416 + 0,909i
Dan kita sudah memiliki bilangan tersebut dalam bentuk binomial. Dari sana kita dapat membuat representasi grafis dalam bidang kompleks . Untuk melakukan ini, perlu dipahami bahwa suatu bilangan kompleks direpresentasikan dalam bidang kompleks dengan menggunakan koordinat bagian nyata pada absis (sumbu x) dan bagian imajiner pada sumbu y (y).
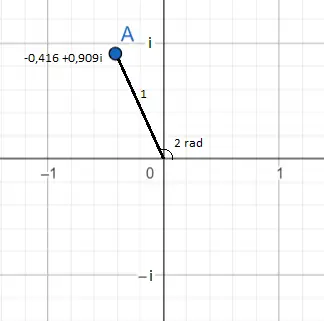
Pada gambar sebelumnya ditampilkan bilangan kompleks e 2i yang sama dengan -0,416 + 0,909i. Hal ini dapat dilihat sebagai titik berwarna biru. Letaknya di pesawat bisa dilihat dari dua sudut .
Yang pertama dan paling jelas adalah dengan representasi bilangan dalam bentuk binomial : -0,416 (pada absis) dan 0,909 (pada komputer). Dan yang kedua berbentuk eksponensial : modul e 2i sama dengan 1, karena itu bilangan yang ada di depan e (karena tidak ada bilangan di depan e, maka kita bayangkan ada 1) dan di eksponennya ada 2, maka argumen atau sudutnya setara dengan dua radian.
Jika Anda kurang memahami paragraf terakhir ini , kami sarankan Anda membaca artikel kami tentang bilangan kompleks. Nah, berikut ini kami akan memberikan penjelasan yang sangat mendalam tentang berbagai cara penulisan bilangan kompleks dan semua sifat-sifatnya.
Representasi grafis dari rumus Euler
Pada contoh sebelumnya, Anda dapat melihat bagaimana rumus Euler diterapkan dan bagaimana rumus tersebut direpresentasikan secara grafis dalam bidang kompleks. Namun, jika kita melangkah lebih jauh dan mencoba merepresentasikan fungsi yang ekuivalen dengan rumus Euler, kita akan menemukan sesuatu yang sangat aneh: fungsi tersebut menghasilkan lingkaran berjari-jari 1 :
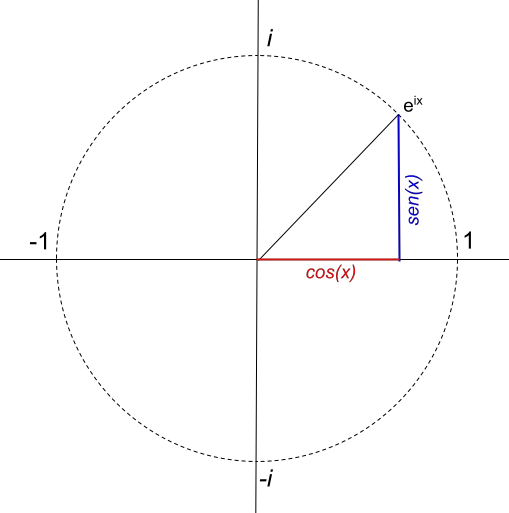
Namun, jari-jari lingkaran secara langsung bergantung pada nilai modulus bilangan kompleks. Misalnya, jika kita ingin merepresentasikan lingkaran dengan jari-jari 4, fungsinya adalah 4e ix . Jadi, fungsinya 4e ix , direpresentasikan seperti ini:
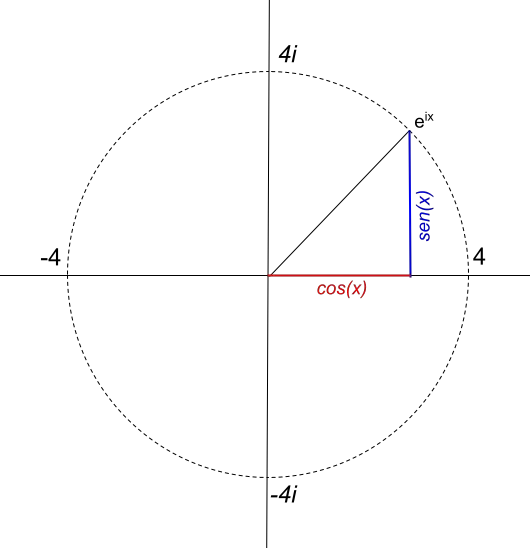
Kembali ke lingkaran berjari-jari 1, jika kita memutuskan untuk menyatakan e iπ (dalam radian), kita harus menghitung terlebih dahulu:
e πi = cos(π) + saya sin(π)
eπi = -1 + saya 0
eπi = -1
Kita memperoleh e πi = -1, yang merupakan identitas Euler yang terkenal.
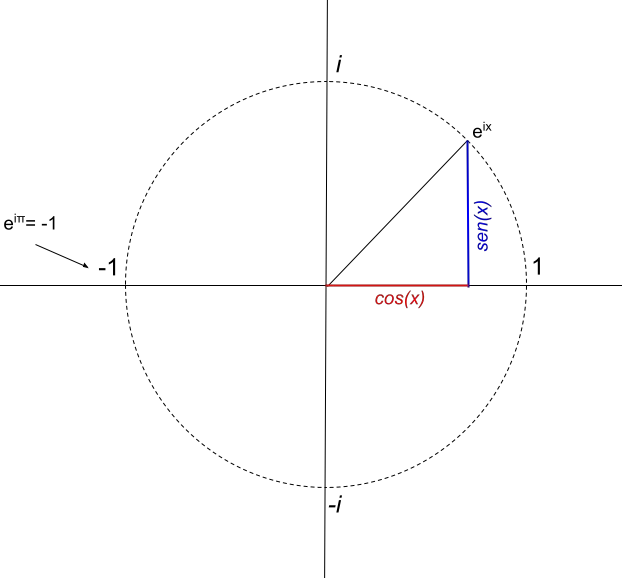
Dari sini kita menyimpulkan bahwa bilangan kompleks e πi hanya mempunyai satu bagian real, yaitu sama dengan -1. Oleh karena itu, representasinya akan sedemikian rupa sehingga:
Penerapan rumus Euler
- Bilangan kompleks: Rumus Euler adalah hubungan antara fungsi trigonometri dan bilangan kompleks. Dari rumus ini, kita dapat menyatakan bilangan kompleks dengan berbagai cara: binomial, eksponensial, dan polar.
- Deret Taylor: Rumus Euler digunakan untuk memperluas fungsi deret Taylor.
- Aljabar Linier: Rumus Euler digunakan dalam diagonalisasi matriks, yang merupakan teknik dasar dalam aljabar linier.
- Kalkulus Diferensial dan Integral: Rumus Euler digunakan dalam penyelesaian persamaan diferensial, yang merupakan teknik yang relevan dalam kalkulus.
Selain itu, ia mempunyai penerapan dalam banyak teori matematika dan bahkan dalam konsep di luar domain matematika, seperti teorema fisika.
kesimpulan
Seperti yang Anda lihat di artikel ini, penerapan rumus Euler yang paling banyak adalah pada bilangan kompleks : dalam ekspresi numerik dan representasinya. Memang benar bahwa ini memiliki beberapa penerapan dalam aljabar, tetapi pada dasarnya Anda bekerja dengan bilangan kompleks. Oleh karena itu, penting untuk memahaminya dengan baik.
Karena itu, kami harap kami dapat membantu Anda memahami konsep ini dengan lebih baik. Dan jika Anda memiliki pertanyaan atau tidak tahu cara melakukan latihan, jangan ragu untuk menulis kepada kami di komentar.