Bilangan desimal sangat penting dalam dunia matematika, tetapi apakah kita benar-benar mengetahui apa itu bilangan desimal dan cara kerjanya? Pada artikel ini kami akan menjelaskan semuanya kepada Anda.
Apa itu bilangan desimal?
Bilangan desimal adalah bilangan bukan bilangan bulat (tidak tercakup dalam himpunan bilangan bulat ), yang mempunyai bagian bilangan bulat dan bagian desimal. Bagian desimal ini ditulis setelah koma dan memungkinkan nilai yang kurang dari satu untuk dinyatakan.
Bilangan desimal adalah cara merepresentasikan bilangan campuran . Memang benar konsep pecahan sangat mirip dengan nilai desimal. Kita dapat melihatnya pada contoh berikut: 7/2 sama dengan 3.5 . Mereka mempertahankan kesetaraan numerik, hanya saja penulisannya berbeda.
Bilangan “3,5” adalah bilangan desimal yang dibaca “tiga koma lima”, bagian bilangan bulatnya adalah 3 dan bagian desimalnya sama dengan 5. Karena bilangan desimal dinyatakan dengan sistem notasi desimal, kita dapat menguraikan bilangan tersebut seperti ini :
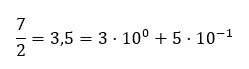
tata nama desimal
Dalam penulisan angka-angka ini, dua jenis notasi yang umum digunakan: notasi standar (atau notasi desimal) dan notasi ilmiah . Yang pertama ini adalah yang paling umum dan yang kami gunakan sejauh ini.
Sedangkan notasi ilmiah merupakan bentuk singkatan dari notasi baku. Dalam notasi ilmiah, bilangan desimal ditulis sebagai bilangan bulat dikalikan pangkat 10 . Misalnya besaran 0,0054 dapat ditulis dalam notasi ilmiah sebagai 5.4 · 10 -3 .
Sedangkan untuk penulisan desimal nonnumerik, kami menggunakan notasi yang mengacu pada posisi yang ditempati setiap angka desimal. Ya, seperti halnya bagian bilangan bulat: satuan, sepuluh, seratus… Bagian desimal memiliki: sepersepuluh, seperseratus, seperseribu…
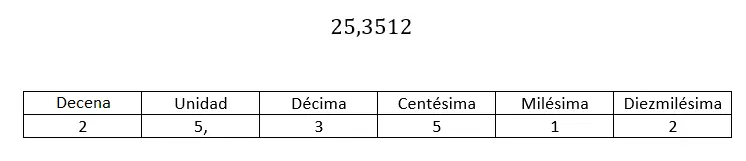
Yang menandai nama setiap digit adalah posisinya dalam kaitannya dengan koma desimal . Dengan cara ini, jika Anda memiliki bilangan desimal dan ingin mengetahui nilai per seratus, Anda harus melihat digit kedua (dari koma desimal, ke kanan). Dalam kasus di atas, seperseratus sama dengan 5.
jenis desimal
Bilangan desimal dapat diklasifikasikan sebagai berikut:
- Desimal tepat: memiliki jumlah tempat desimal yang ditentukan dan terbatas. Misalnya: 9.263.
- Desimal berulang: memiliki jumlah tempat desimal yang tak terhingga.
- Desimal berulang murni: bagian desimal terdiri dari bilangan yang berulang tanpa batas. Misal: 2.1515151515… Sejak 15 berulang tanpa batas waktu.
- Desimal berulang campuran: bagian desimal terdiri dari suatu nilai, diikuti oleh angka lain yang berulang tanpa batas. Misal: 2.4615151515… Karena 46 tidak terulang.
- Desimal tidak berulang: memiliki bagian desimal tak terhingga yang tidak berulang. Di bagian ini kita menemukan beberapa konstanta matematika , akar kuadrat dari dua…

Sifat-sifat bilangan desimal
Bilangan desimal mempunyai beberapa sifat, antara lain:
- Desimal tidak berubah jika angka nol dijumlahkan di sebelah kanannya, sehingga angka 0,25 setara dengan 0,250 dan 0,2500. Pada dasarnya, karena mereka menyatakan jumlah yang sama.
- Desimal setara dengan pecahan, misalnya setengah satuan (1/2) dilambangkan dengan 0,5.
- Jika kita mengalikan atau membagi suatu bilangan desimal dengan pangkat sepuluh, kita harus memindahkan koma desimalnya: ke kanan jika kita mengalikan dan ke kiri jika kita membagi.
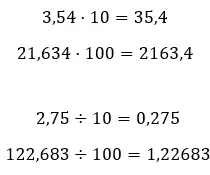
- Anda dapat menyederhanakan suatu bilangan desimal, caranya dengan membulatkan bilangan desimal tersebut . Metode ini terdiri dari menyatakan angka desimal lebih sedikit, memodifikasi nilai angka sesedikit mungkin. Jika Anda ingin mempelajari cara menggunakan sistem penyederhanaan ini, kami menyarankan Anda memasukkan tautan terakhir ini.
Representasi angka desimal
Himpunan desimal dapat direpresentasikan pada garis bilangan seperti himpunan lainnya.
Berangkat dari fakta bahwa desimal memiliki bagian bilangan bulat dan tempat desimal (kurang dari satu), kita dapat menyimpulkan bahwa desimal direpresentasikan di antara bilangan bulat . Misalnya, antara angka 0 dan 1, terdapat angka desimal yang tak terhingga. Di bawah ini Anda dapat melihatnya terwakili dalam baris:
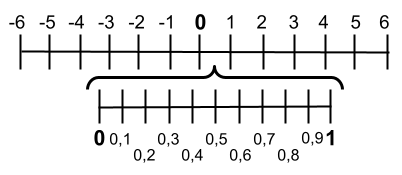
Seperti yang Anda lihat pada gambar, kami telah menulis persepuluhan antara 0 dan 1. Meskipun di antara kedua angka ini terdapat tempat desimal tak terhingga , representasi yang sangat kompleks dapat dibuat. Terlebih lagi, hal ini tidak hanya terjadi antara 0 dan 1, namun terjadi di antara semua bilangan bulat.
Operasi pada bilangan desimal
Pengoperasian bilangan desimal mirip dengan bilangan bulat. Satu-satunya perbedaan adalah posisi digit desimal harus diperhitungkan. Oleh karena itu, sebelum menyelesaikan suatu operasi, Anda harus memastikan bahwa Anda selalu mengerjakan bilangan yang sama : persepuluhan dengan persepuluhan, perseratus dengan perseratus…
Selanjutnya, kita akan melakukan tinjauan singkat tentang empat operasi aritmatika dasar dengan desimal:
- Penambahan desimal:

- Pengurangan angka desimal:

- Perkalian desimal:

- Pembagian desimal:

Penggunaan dan penerapan angka desimal
Bilangan desimal banyak digunakan dalam kehidupan sehari-hari dan matematika. Misalnya, ketika Anda membeli sesuatu di toko, Anda perlu mengetahui harga barang yang Anda beli, dan harga tersebut akan dinyatakan dalam angka desimal. Selain itu, mereka digunakan untuk mengukur jarak, berat dan aspek kehidupan sehari-hari lainnya.
Dalam matematika, bilangan desimal memungkinkan kita dengan mudah menyatakan besaran yang sangat kecil atau sangat besar. Dan mereka juga memungkinkan kita membuat perhitungan dengan lebih presisi . Misalnya, jika kita ingin menghitung setengah dari 3 satuan, kita dapat membaginya menjadi dua bagian yang sama besar dan mendapatkan 1,5 satuan.