Pada artikel ini kami akan menjelaskan apa itu fungsi invers (atau timbal balik) dan cara menghitung invers suatu fungsi. Anda juga akan menemukan cara mudah mengetahui apakah suatu fungsi memiliki invers atau tidak dan sifat-sifat dari jenis fungsi tersebut. Terakhir, Anda dapat berlatih dengan latihan langkah demi langkah tentang fungsi invers.
Apa fungsi inversnya?
Fungsi invers, disebut juga fungsi timbal balik, adalah fungsi yang domainnya merupakan rentang fungsi lain (fungsi asal) dan rentangnya merupakan domain fungsi asal. Fungsi invers dari fungsi f dinyatakan dengan simbol f -1 .
Oleh karena itu, fungsi invers dari f(x) adalah fungsi yang memenuhi kondisi berikut:
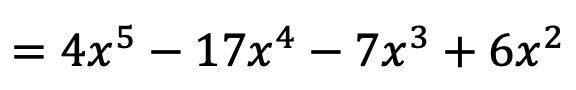
Emas
![]()
adalah fungsi kebalikan dari
![]()
Konsep fungsi invers juga dapat didefinisikan dengan menggunakan komposisi fungsi, karena setiap fungsi yang tersusun dengan fungsi inversnya sama dengan fungsi identitas:
![]()
➤ Lihat: apa itu komposisi fungsi?
Jadi kalau persamaan sebelumnya terpenuhi berarti demikian
![]()
adalah fungsi invers (atau fungsi timbal balik) dari
![]()
Contoh fungsi invers
Mengingat definisi fungsi invers, mari kita selesaikan sebuah contoh untuk lebih memahami maknanya.
- Tentukan apakah fungsi-fungsi berikut merupakan invers satu sama lain:
![]()
Jika kedua fungsi tersebut saling invers, maka terpenuhi 2 syarat berikut:
![]()
Jadi mari kita periksa apakah kedua persamaan terpenuhi. Kita periksa dulu
![]()
![Rendered by QuickLaTeX.com \begin{aligned} \displaystyle\left(f \circ g\right)(x)& = f\Big(g(x)\Big)\\[2ex]&= f\left( \frac{x-1}{2} \right)\\[2ex]& = 2\left( \frac{x-1}{2} \right)+1\\[2ex]& =x-1+1\\[2ex]&=\bm{x} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-36f7d5f4d815a58f808114ae471c31dd_l3.png)
➤ Jika Anda belum memahami perhitungan yang baru saja kami lakukan, Anda perlu membuka tautan di atas untuk mengetahui komposisi fungsinya? , kami menjelaskan cara menyelesaikan jenis operasi ini dengan fungsi.
Sehingga
![]()
ya, itu tercapai. ✅
Sekarang mari kita periksa kesetaraannya
![]()
![Rendered by QuickLaTeX.com \begin{aligned} \left(g \circ f\right)(x)&= g\Big(f(x)\Big)\\[2ex]&= g\Big(2x +1 \Big)\\[2ex]&=\cfrac{(2x+1)-1}{2}\\[2ex]&= \cfrac{2x}{2}\\[2ex]&=\bm{x} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-83423fe7deab472f1a7e9575ec7af8c4_l3.png)
Dan kondisi invertibilitas
![]()
itu juga tercapai. ✅
Kesimpulannya, karena kedua persamaan tersebut berlaku, kedua fungsi tersebut merupakan invers satu sama lain.
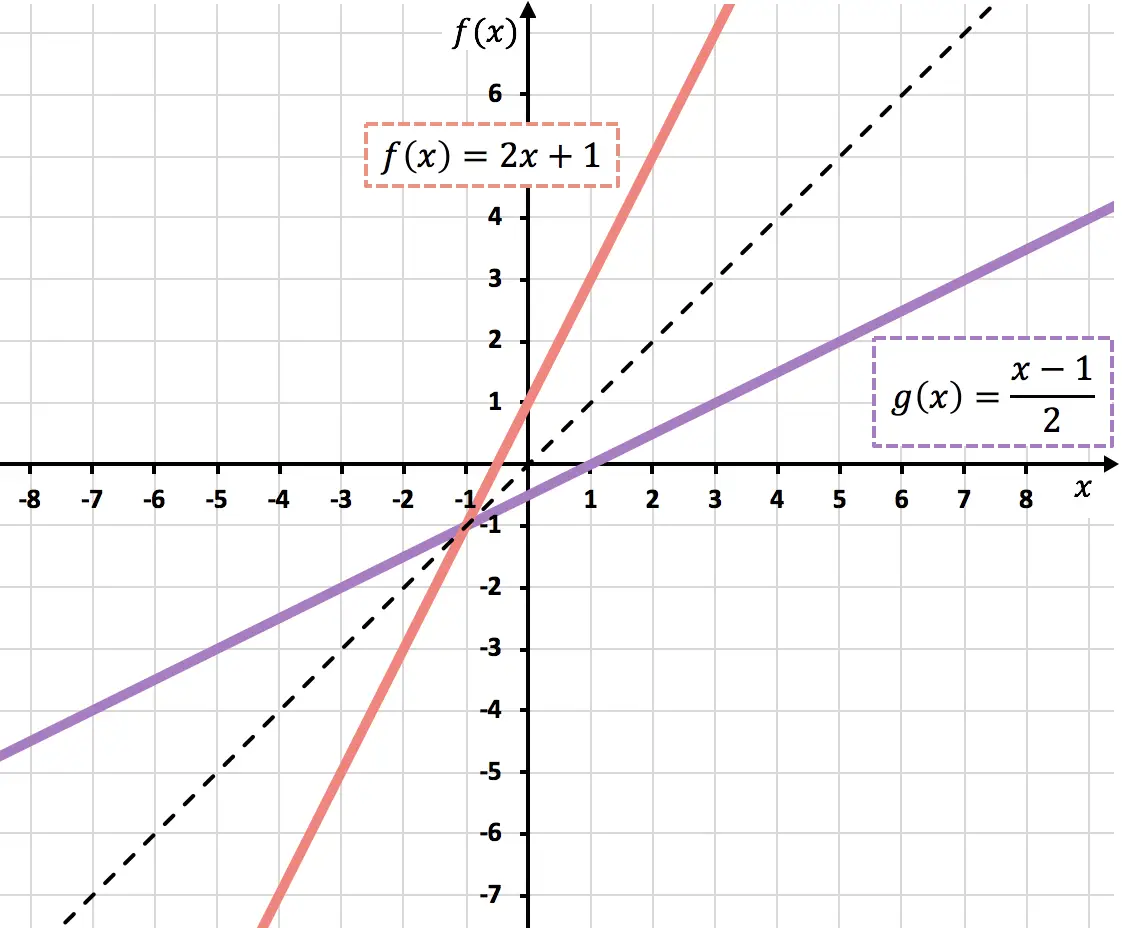
Di bawah ini Anda dapat melihat kedua fungsi tersebut dalam grafik. Perhatikan bahwa grafik dua fungsi invers adalah simetris terhadap garis bagi kuadran pertama dan ketiga:
Bagaimana cara mengetahui apakah suatu fungsi mempunyai invers
Suatu fungsi memiliki fungsi invers jika merupakan fungsi injektif , yaitu jika setiap nilai di seluruh domainnya berkorespondensi dengan satu nilai dalam intervalnya.
Fungsi eksponensial dengan fungsi invers

Fungsi kuadrat tanpa fungsi invers

Misalnya, fungsi eksponensial kiri memiliki fungsi invers karena setiap x berhubungan dengan satu nilai f(x) . Sebaliknya, fungsi kuadrat siku-siku tidak memiliki fungsi invers karena memiliki beberapa nilai x yang bayangannya sama (misalnya f(1)=f(3)=2) .
Demikian pula fungsi bijektif terdiri dari fungsi injektif dan dugaan, oleh karena itu setiap fungsi bijektif juga mempunyai fungsi invers.
Di sisi lain, perlu diingat bahwa invers fungsi tidak sama dengan invers perkalian suatu fungsi , melainkan dua konsep yang berbeda. Untuk mencari invers perkalian suatu fungsi, cukup hitung 1 korespondensi dengan fungsi tersebut.
![]()
Pada bagian selanjutnya kita akan melihat cara menentukan fungsi invers.
Cara mencari fungsi invers
Untuk menghitung invers suatu fungsi, langkah-langkah berikut harus dilakukan:
- Gantikan f(x) dengan y .
- Ubah semua x menjadi y , dan sebaliknya.
- Hapus variabel y .
- Gantikan variabel y dengan f -1 (x) . Fungsi invers adalah ekspresi yang ditemukan untuk f -1 (x) .
Agar Anda dapat melihat secara pasti bagaimana cara menghitung invers fungsi, kita akan menentukan invers fungsi berikut sebagai contoh:
![]()
Pertama-tama, kita perlu menggantinya
![]()
Untuk
![]()
:
![]()
Sekarang kami mengubah segalanya
![]()
dari fungsi oleh
![]()
, dan sebaliknya:
![]()
Kemudian kita menghapus variabelnya
![]()
![]()
![]()
![]()
![]()
Dan terakhir, fungsi kebalikan dari
![]()
adalah ekspresi aljabar yang kita peroleh dengan mengisolasi
![]()
![]()
Soal latihan fungsi invers
Di bawah ini kami telah menyiapkan beberapa latihan langkah demi langkah tentang fungsi invers agar Anda dapat berlatih.
👉 Ingatlah bahwa jika Anda tidak memahami cara menyelesaikan suatu latihan atau ingin kami menyelesaikan masalah untuk Anda, Anda dapat menulis kepada kami di komentar!
Latihan 1
Periksa apakah dua fungsi berikut invers (atau timbal balik) atau tidak:
![]()
Agar kedua fungsi tersebut invers satu sama lain, hal berikut ini harus benar:
![]()
Oleh karena itu perlu dilakukan pengecekan apakah kedua syarat tersebut terpenuhi. Kita periksa dulu
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle\left(f \circ g\right)(x)&= f\Big(g(x)\Big)\\[2ex]&= f\left( \frac{x+7}{3} \right)\\[2ex]&= 3 \left(\frac{x +7}{3} \right) - 7 \\[2ex] & =x + 7 - 7 \\[2ex]&= \bm{x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fbbdf5bb2c308a1973c5f2d99e822ad5_l3.png)
Belum,
![]()
ya, itu tercapai. ✅
Sekarang mari kita periksa komposisi fungsi lainnya
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\left(g \circ f\right)(x)&= g\Big(f(x)\Big)\\[2ex]&= g\left(3x-7\right)\\[2ex]&=\cfrac{(3x-7)+7}{3}\\[2ex]&=\cfrac{3x}{3}\\[2ex]&=\bm{x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ac5819584c8358b812c8214a902e4f08_l3.png)
Dimana
![]()
itu juga tercapai. ✅
Bagaimana hal itu bisa terjadi
![]()
Dan
![]()
, kedua fungsi tersebut berbanding terbalik satu sama lain.
Latihan 2
Hitung invers (atau fungsi timbal balik) dari fungsi polinomial derajat pertama berikut:
![]()
Hal pertama yang harus dilakukan untuk membalikkan fungsi adalah dengan mengganti sukunya
![]()
Untuk
![]()
![]()
Sekarang kita mengubah
![]()
oleh
![]()
, dan sebaliknya:
![]()
Dan kemudian kami melepaskannya
![]()
![]()
![]()
![]()
![]()
Kami sudah berhasil merilisnya
![]()
. Oleh karena itu, kebalikan dari fungsi
![]()
Timur:
![]()
Latihan 3
Balikkan fungsi polinomial kuadrat berikut:
![]()
Untuk mencari fungsi invers kita akan mengikuti prosedur yang kita lihat di atas. Jadi kami akan menelepon
![]()
ke fungsinya
![]()
![]()
Kedua, kami memodifikasi
![]()
Untuk
![]()
, dan sebaliknya:
![]()
Dan terakhir, kami mengisolasi variabelnya
![]()
![]()
![]()
![]()
![]()
Namun dalam hal ini fungsi yang diperoleh memiliki dua citra untuk setiap elemen domainnya (citra positif dan citra negatif). Oleh karena itu, tidak ada fungsi invers dari fungsi masalah.
Latihan 4
Tentukan fungsi invers (atau fungsi timbal balik) dari fungsi rasional berikut:
![]()
Pertama, kita ganti
![]()
Untuk
![]()
![]()
Sekarang kita mengubah
![]()
pembilang dan penyebut
![]()
, dan sebaliknya:
![]()
Dan kemudian kami melepaskannya
![]()
![]()
Ekspresi
![]()
membagi seluruh ruas kanan persamaan, sehingga kita dapat mengalikannya dengan mengalikan seluruh ruas kiri persamaan:
![]()
![]()
Kami menyetujui semua persyaratan
![]()
di satu sisi persamaan, dan suku lain di sisi lain:
![]()
Untuk membersihkan
![]()
, kita mengekstrak faktor persekutuan dari ruas kiri persamaan:
![]()
Dan sebagai tukang pos
![]()
adalah mengalikan seluruh ruas kiri persamaan, kita dapat melakukannya dengan membagi seluruh ruas kanan:
![]()
Kami sudah berhasil merilisnya
![]()
. Jadi fungsi invers dari
![]()
Timur:
![]()
Sifat-sifat fungsi invers
Fungsi invers mempunyai ciri-ciri sebagai berikut:
- Fungsi invers bersifat unik, yaitu jika suatu fungsi dapat dibalik, maka untuk fungsi tersebut hanya terdapat satu fungsi invers.
- Domain dari fungsi invers adalah jangkauan (atau jangkauan) dari fungsi aslinya.
- Demikian pula, jalur fungsi invers ekuivalen dengan domain fungsi aslinya.
- Setiap fungsi yang tersusun dari fungsi inversnya menghasilkan fungsi identitas (x).
![]()
- Grafik suatu fungsi dan grafik invers fungsi tersebut simetris terhadap garis bagi kuadran pertama dan ketiga.
- Invers dari fungsi invers sama dengan fungsi aslinya:
![]()
- Membalik fungsi komposit sama dengan menghitung invers setiap fungsi secara terpisah dan kemudian menyusun fungsi inversnya.
![]()
- Suatu fungsi kontinu secara simultan dengan fungsi inversnya, atau dengan kata lain jika suatu fungsi kontinu maka invers fungsi tersebut juga demikian.
- Jika suatu fungsi terdiferensiasi dan turunannya tidak hilang sewaktu-waktu
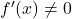
, fungsi inversnya juga akan terdiferensiasi.
Selain itu, turunan fungsi invers dapat dihitung dengan menerapkan teorema fungsi invers , yang rumusnya adalah:
![]()