Notasi matematika adalah cara mengkomunikasikan ide dan perhitungan melalui penggunaan simbol. Meski sekilas terlihat membingungkan, namun dengan sedikit latihan Anda akan bisa menafsirkannya dengan mudah. Pada artikel ini kami akan menunjukkan kepada Anda arti dari semua simbol yang digunakan dalam notasi ini dan beberapa contoh penerapannya.
Apa itu notasi matematika?
Notasi matematika adalah cara penulisan nilai dan ekspresi yang digunakan dalam matematika. Teknik ini memungkinkan matematikawan menyatakan gagasan secara ringkas dan tepat . Notasi matematika juga memungkinkan mereka yang berlatih atau mempelajari matematika untuk lebih memahami konsep.
Bahasa matematika tidak sama dengan notasi ilmiah, yaitu cara penulisan nilai numerik. Sedangkan notasi matematika lebih merupakan sekumpulan simbol yang memungkinkan Anda menulis ekspresi kompleks, seperti halnya bahasa. Kami akan kembali ke topik ini secara lebih rinci nanti.
Bagaimana cara membaca notasi matematika?
Belajar menafsirkan notasi matematika lebih mudah dari yang terlihat, Anda hanya perlu mempelajari arti setiap simbol dan setelah melakukannya, Anda akan dapat membaca apa pun yang ditulis dalam notasi matematika. Sesederhana itu, meski jelas membutuhkan latihan dan banyak waktu belajar.
Ekspresi matematika sangat logis dan selalu mengikuti pola, oleh karena itu, Anda hanya perlu menghafal aturannya dan kemudian Anda akan tahu cara mengekstrapolasinya ke situasi apa pun. Kita bahkan dapat mendeskripsikan perhitungan yang sangat rumit, inilah keajaiban bahasa matematika, yang memungkinkan pesan yang sangat rumit dikomunikasikan dengan cara yang metodis.
Komponen Notasi Matematika
Notasi matematika terdiri dari serangkaian simbol yang mewakili bilangan, operasi, dan hubungan di antara keduanya. Simbol-simbol ini mungkin tampak rumit pada awalnya, namun dengan sedikit latihan dan pemahaman, menafsirkan notasi matematika akan menjadi permainan anak-anak.
Selanjutnya akan dijelaskan secara detail keempat jenis unsur yang terdapat dalam bahasa matematika. Dimulai dari yang paling dasar dan diakhiri dengan yang paling kompleks dan abstrak. Dan setelah penjelasan teoritis selesai, kita akan membahas tentang jenis-jenis notasi numerik yang ada.
Angka dan kumpulan angka
Pertama-tama, kita harus mendefinisikan bilangan matematika , itu adalah konsep matematika yang menunjukkan besaran yang berhubungan dengan suatu satuan. Kita dapat mendeskripsikan nilai numerik apa pun, mengikuti sistem penomoran desimal dan menggabungkan simbol-simbol berikut: 0, 1, 2, 3, 4, 5, 6, 7, 8, dan 9.
Jika kita mengurutkan bilangan menurut sifat yang berbeda, kita mendapatkan beberapa kategori bilangan, yang disebut himpunan bilangan. Dan kelompok nilai ini juga mempunyai simbol tersendiri yang melambangkannya, pada daftar berikut ini kami sajikan semuanya dengan nama kelompok yang bersangkutan:
- ℙ: bilangan prima
- ℕ: bilangan asli
- ℤ: Utuh
- ℚ: bilangan rasional
- ℝ: Bilangan real
- 𝕀 : bilangan imajiner
- ℂ: bilangan kompleks
- ℍ: Angka empat
Simbol-simbol ini umumnya digunakan dalam perhitungan kita, untuk menentukan rentang angka yang luas, sekaligus. Misalnya, jika kita memiliki ekspresi yang menerima banyak nilai, daripada menuliskan angka satu per satu, akan lebih mudah bagi kita untuk menentukan nilai tersebut melalui simbol yang sesuai dengan grup numeriknya .
Operator dan pembilang
Sekarang kita telah membahas bilangan yang merupakan inti dari matematika, kita perlu membahas tentang operator dan bilangan . Yang pertama adalah simbol-simbol yang memungkinkan kita merepresentasikan suatu operasi: penjumlahan (+), pengurangan (-), perkalian (x atau ·), pembagian (ulir), dan lain-lain.
Namun, kami juga memiliki dua jenis operator lainnya, yaitu operator logika dan operator relasional. Yang pertama menyatakan konjungsi, disjungsi dan negasi. Mereka membantu kita mengusulkan operasi logika , yang, tidak seperti operasi aritmatika, tidak bekerja dengan angka, tetapi dengan proposisi matematika.
Sedangkan yang kedua memungkinkan kita membangun kesetaraan dan hubungan antar nilai atau ekspresi matematika. Simbol-simbol ini dapat digunakan dalam perhitungan aritmatika (untuk mengurutkan angka), tetapi simbol-simbol ini lebih penting dalam aljabar, ketika kita memiliki variabel (lebih lanjut tentang ini dalam dua bagian).
Dalam daftar berikut Anda dapat menemukan definisi semua operator yang telah kita bahas sejauh ini:
| Simbol | Definisi | Baik |
| + | Tambahan | operator aritmatika |
| – | Pengurangan | operator aritmatika |
| X, *, · | Perkalian | operator aritmatika |
| − | Divisi | operator aritmatika |
| x² | Pemberdayaan | operator aritmatika |
| √ | menyetorkan | operator aritmatika |
| DAN | Konjungsi | operator logis |
| SALAH SATU | Pemisahan | operator logis |
| TIDAK | Penyangkalan | operator logis |
| = | Sama dengan | operator relasi |
| > | Lebih besar dari | operator relasi |
| < | Lebih kecil dari | operator relasi |
| >= | Lebih baik dari atau sama | operator relasi |
| <= | kurang dari atau sama dengan | operator relasi |
| ≠ | tidak sama dengan | operator relasi |
| ≡ | Persis sama | operator relasi |
| ≈ | hampir sama | operator relasi |
| ≃ | Setara dengan | operator relasi |
| ∝ | Sebanding | operator relasi |
Meskipun ada juga lima operator logika lainnya yang digunakan untuk menjelaskan logika matematika dari teori himpunan. Yang merupakan cabang yang menerapkan logika himpunan , yang digunakan dalam perhitungan, geometri, statistik… Kemudian, kami tunjukkan simbol-simbol yang digunakan dan definisinya.
| Simbol | Definisi |
| x ∈ A | x milik A |
| x ∉ A | x bukan milik A |
| ∪ | Persatuan |
| ∩ | Persimpangan |
| ⊂ | Penyertaan |
Sedangkan untuk bilangan, kita dapat mendefinisikannya sebagai simbol yang menunjukkan banyaknya elemen suatu himpunan yang memenuhi kondisi tertentu (kesetaraan, keteraturan, keanggotaan, dll.). Ada berbagai macam operator, tetapi di antara yang paling banyak digunakan, kami dapat menyoroti:
| Simbol | Definisi | Baik |
| ∀x | untuk semua x | mengukur |
| ∃x | Setidaknya ada satu x | mengukur |
| ∄x | tidak ada x | mengukur |
| ∃!x | Hanya ada satu x | mengukur |
| | | Seperti | mengukur |
| ∴ | JADI | mengukur |
Ekspresi matematika dan hubungannya
Dengan simbol-simbol yang telah kita bahas sejauh ini, Anda dapat memahami banyak hal matematika, namun kami belum menjelaskan penerapan atau hubungannya dalam ekspresi kompleks, seperti operasi gabungan atau perhitungan aljabar. Ditambah lagi, masih ada simbol hubungan yang perlu dibicarakan. Inilah yang akan kita lihat di bagian ini.
Mulai dari simbol pengelompokannya yaitu tanda kurung, tanda kurung siku, dan kurung kurawal. Elemen-elemen ini penting dalam penunjukan rumus yang kompleks. Fungsi utamanya adalah memberikan prioritas pada perhitungan tertentu, dalam ekspresi global. Dan terdapat tingkat prioritas yang berbeda di antara ketiga jenis tersebut. Pada ungkapan ini terlihat urutan penulisan 3 {[2 + (3 – 2) · 2] – 4}.
| simbol | Definisi | Prioritas |
| “(“Dan”)” | Kurung | Prioritas maksimum |
| “[“Dan”]” | Kurung | prioritas kedua |
| “{” Dan “}” | Kunci | prioritas ketiga |
Dan untuk menyelesaikan kategori ini, kita akan membahas tentang penjumlahan (Σ) dan hasil kali (∏) , yang merupakan elemen yang memungkinkan kita mendeskripsikan penjumlahan dan perkalian berulang. Penjumlahannya sama dengan mengatakan: “jumlah Xi, dimana i mengambil nilai dari 1 sampai an”. Dan hasil perkaliannya sama, tetapi alih-alih menjumlahkan, kita mengalikannya.
analisis aljabar
Hal pertama yang dibahas tentang simbol aljabar adalah variabel yang diwakili oleh huruf alfabet. Fungsinya untuk meniru suatu bilangan , tetapi tidak mempunyai nilai tetap seperti konstanta matematika , sehingga dapat mengambil nilai baru. Ini berlaku untuk persamaan, limit, turunan, integral, matriks…
Terakhir, kita ingin membahas tentang representasi semua operasi aljabar yang baru saja kita bahas di paragraf terakhir ini. Sejak itu, mereka menjadi dasar aljabar dan Anda perlu mengetahui apa simbologinya. Selanjutnya, kami tunjukkan tabel dengan simbol berbeda dan definisi singkat:
| Simbol | Definisi |
| lim x → b | Limit (ketika x cenderung ke arah b) |
| y’, ƒ’ (x), dy/dx | turunan |
| ∫ | Menyelesaikan |
| Ke mxn | Matriks dimensi mxn |
Kesimpulan tentang simbol-simbol bahasa matematika
Sejauh ini Anda telah melihat semua simbol penting yang dibahas dalam matematika, masih banyak lagi yang perlu didiskusikan. Namun, ini lebih spesifik untuk setiap subkategori matematika: geometri, statistik, aljabar… Oleh karena itu, kami akan menutup subjek ini dan membahas tentang notasi numerik.
Jenis notasi numerik
Di bagian ini kita akan melihat semua cara untuk menyatakan bilangan matematika, karena terdapat notasi berbeda untuk melakukannya. Pada awalnya, kami telah menyebutkan sistem bilangan desimal di atas, yang paling banyak digunakan oleh ahli matematika. Selanjutnya kami akan menjelaskannya lebih detail dan menunjukkan jenis notasi matematika lainnya:
notasi desimal
Sistem bilangan desimal adalah sistem bilangan posisi (sistem di mana posisi setiap digit akan menentukan nilainya) didasarkan pada kelipatan dan subkelipatan dari angka 10. Karena sepuluh adalah angka yang digunakan sebagai basis numerik . Oleh karena itu, sepuluh simbol angka yang akan kita gunakan adalah: 1, 2, 3, 4, 5, 6, 7, 8, 9 dan 0.
Nilai angka-angka ini ditentukan dari penjumlahan angka-angka tersebut dikalikan dengan pangkat pada basis sepuluh, yang ditetapkan menurut kedudukannya . Dan penting sekali untuk Anda ingat bahwa untuk menulis angka kurang dari satu, Anda harus menggunakan koma desimal. Di bawah ini contohnya:
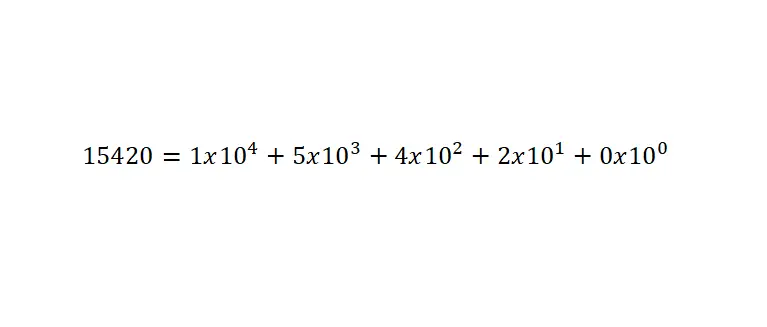
Notasi ilmiah
Notasi bentuk eksponensial atau notasi ilmiah jelas merupakan salah satu jenis tulisan yang paling banyak digunakan dalam ilmu pengetahuan dan teknologi. Memang, ini memungkinkan kita untuk menyatakan bilangan yang sangat besar dan sangat kecil dengan cara yang sederhana. Untuk memahami pengertian notasi ilmiah, kami akan menjelaskan cara meneruskan bilangan bulat ke notasi ini:
- Memindahkan koma desimal: Anda harus memindahkan koma desimal sebanyak yang diperlukan hingga Anda mencapai digit pertama (ke kiri jika Anda memiliki bilangan yang sangat besar dan ke kanan jika Anda memiliki bilangan yang sangat kecil).
- Tetapkan basisnya: tulis bilangan terakhir ini dikalikan sepuluh, jadi, di samping nilai yang Anda peroleh dengan memindahkan koma desimal ke satu sisi, Anda harus menulis perkalian dengan sepuluh: “x 10”.
- Tambahkan eksponen: dengan nilai yang sama dengan berapa kali Anda memindahkan koma desimal. Untuk bilangan besar, eksponennya dibiarkan positif, tetapi untuk bilangan kecil, eksponennya harus ditulis dengan tanda negatif.
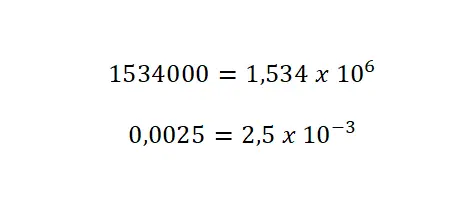
notasi heksadesimal
Sistem heksadesimal didasarkan pada 16, artinya menggunakan enam belas simbol berbeda: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E dan F Sebisa mungkin lihat, sistem penomoran ini terdiri dari angka sistem desimal dan enam huruf. Notasi ini umumnya digunakan khususnya di bidang IT dan segala sesuatu yang berhubungan dengan IT.
Penting untuk diperjelas bahwa karena memiliki simbol yang sama dengan jenis notasi lainnya, kita harus selalu menunjukkan bahwa notasi tersebut ditulis dalam heksadesimal melalui tanda kurung dan indeks 16 . Dalam contoh berikut, Anda dapat melihat contoh yang sangat jelas tentang konversi bilangan heksadesimal ke notasi desimal:
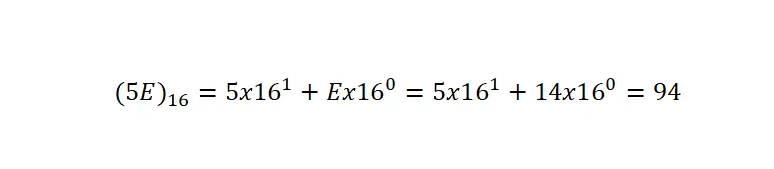
Untuk mengonversi bilangan heksadesimal menjadi ekspresi desimal, kita perlu memecah bilangan tersebut menjadi perkalian basisnya, seperti yang kita lakukan pada notasi desimal, namun mengubah basisnya menjadi 16 . Selanjutnya, kita akan mengalikan setiap digit dengan enam belas yang dipangkatkan ke posisi dimana digit tersebut menempati minus satu.
notasi oktal
Sistem terakhir yang akan kita bahas adalah notasi oktal yang mempunyai basis 8. Artinya hanya menggunakan delapan simbol atau angka: 0, 1, 2, 3, 4, 5, 6, dan 7. adalah yang paling sedikit digunakan sistem penomoran dari semua yang telah kami jelaskan. Perlu dicatat bahwa konversi notasi ini dilakukan dengan prosedur yang sama seperti prosedur sebelumnya.
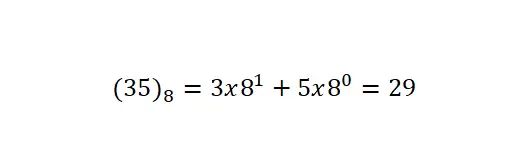
notasi baru
Terakhir, kita dapat berbicara tentang sistem angka Romawi , yang tidak banyak digunakan saat ini, tetapi pada masa lalu sangat penting dalam bidang matematika. Karena itu adalah salah satu notasi yang menghidupkan matematika.
Tulisan anda dibatasi 7 simbol : I (1), V (5), X (10), L (50), C (100), D (500) dan M (1000). Dan dengan menggabungkan huruf-huruf ini, semua angkanya ditulis. Jika Anda ingin mengetahui bagaimana gabungannya sehingga menghasilkan angka lain yang lebih besar, kami sarankan membaca artikel kami tentangnya, mengakses melalui tautan terakhir.
Bagaimana cara meningkatkan kinerja membaca dalam notasi matematika?
Ada beberapa cara untuk meningkatkan kinerja dalam membaca notasi matematika. Salah satu caranya adalah dengan membaca simbol dan angka dengan lantang. Cara lainnya adalah dengan mengenal simbol dan maknanya. Anda juga dapat berlatih membaca notasi matematika menggunakan latihan dan soal.
Kami harap kami membantu Anda dengan panduan ini, jika Anda memiliki pertanyaan, jangan ragu untuk menuliskannya di komentar . Atau jika Anda ingin memberikan kontribusi mengenai topik ini, kami berharap dapat melihatnya di komentar juga. Oleh karena itu, kami meninggalkan artikel untuk Anda tentang cara belajar matematika , jika Anda ingin terus membaca.