Halaman ini menjelaskan apa itu transformasi fungsi dan cara menemukannya. Ada tiga jenis transformasi: translasi (atau perpindahan), simetri, dan ekspansi (atau kontraksi). Anda juga akan menemukan latihan diselesaikan langkah demi langkah sehingga Anda dapat berlatih dan memahami konsep tanpa meninggalkan keraguan.
Apa yang dimaksud dengan transformasi fungsi?
Terkadang kita mungkin diminta untuk membuat grafik fungsi dasar yang sangat mirip dengan fungsi lain yang sudah kita ketahui. Nah, daripada merepresentasikan fungsi serupa lagi, teknik dapat digunakan untuk beralih dari merepresentasikan satu fungsi ke fungsi lainnya dengan mudah dan cepat.
Jadi, transformasi fungsi adalah teknik yang memungkinkan perpindahan dari representasi grafis suatu fungsi ke representasi grafis dari fungsi lain yang sangat mirip melalui operasi dasar.
Pada dasarnya ada tiga jenis transformasi fungsi dasar:
- Terjemahan atau pergerakan : suatu fungsi dapat dipindahkan secara vertikal dan horizontal.
- Pemantulan atau kesimetrian : Suatu fungsi dapat dicerminkan dengan menggunakan sumbu X atau sumbu Y sebagai sumbu simetrinya.
- Ekspansi dan kompresi : Suatu fungsi dapat diperbesar atau diperkecil.
Setelah kita melihat konsep transformasi suatu fungsi, kita akan mempelajari lebih dalam setiap jenis modifikasinya.
Terjemahan atau perpindahan fungsi
Kita akan mulai dengan peralihan fungsi. Ada dua jenis: terjemahan vertikal dan terjemahan horizontal.
Terjemahan atau pergerakan vertikal suatu fungsi
Untuk menerjemahkan atau memindahkan suatu fungsi secara vertikal (sepanjang sumbu Y), Anda harus menambah atau mengurangi konstanta ke fungsi tersebut:
Kita menaikkan fungsi k satuan dengan menambahkan ka ke fungsi tersebut:
![]()
Kita menggeser suatu fungsi k satuan ke bawah dengan mengurangkan ka dari fungsi tersebut:
![]()
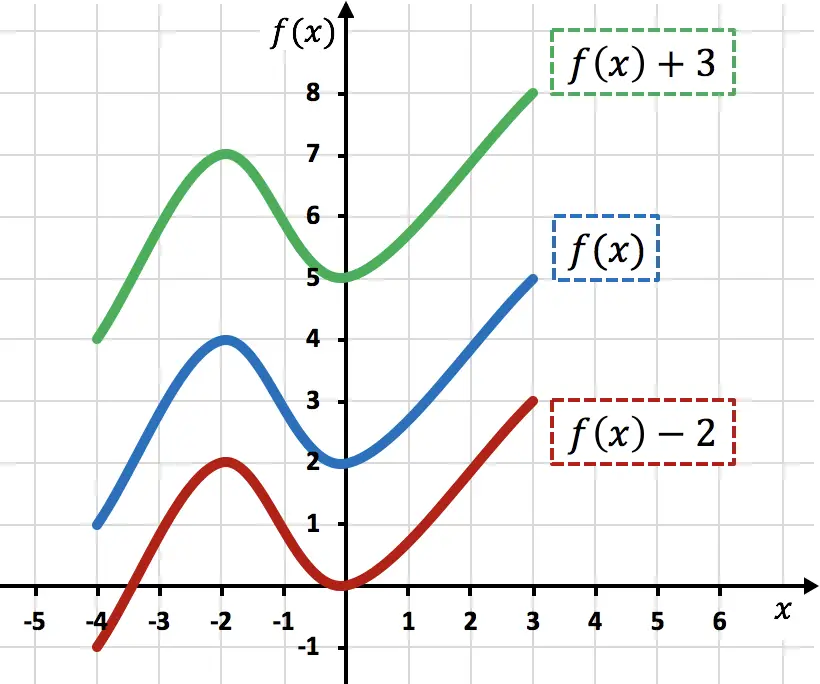
Seperti yang Anda lihat dari grafik, menambahkan konstanta ke fungsi apa pun akan menggeser unit yang ditambahkan ke atas (fungsi hijau). Sebaliknya, saat mengurangkan suatu bilangan dari suatu fungsi, satuan yang dikurangi akan dipindahkan ke bawah (fungsi merah).
Perhatikan bahwa dalam jenis pergerakan ini hanya koordinat Y dari titik-titik fungsi yang diubah, sedangkan koordinat X tetap sama.
Terjemahan atau perpindahan fungsi secara horizontal
Untuk menerjemahkan atau menggeser suatu fungsi secara horizontal (sepanjang sumbu X), Anda harus menambah atau mengurangi sebuah konstanta pada variabel bebas x :
Grafik dari
![]()
adalah grafik dari
![]()
memindahkan k unit ke kiri.
Grafik dari
![]()
adalah grafik dari
![]()
menggeser k satuan ke kanan.
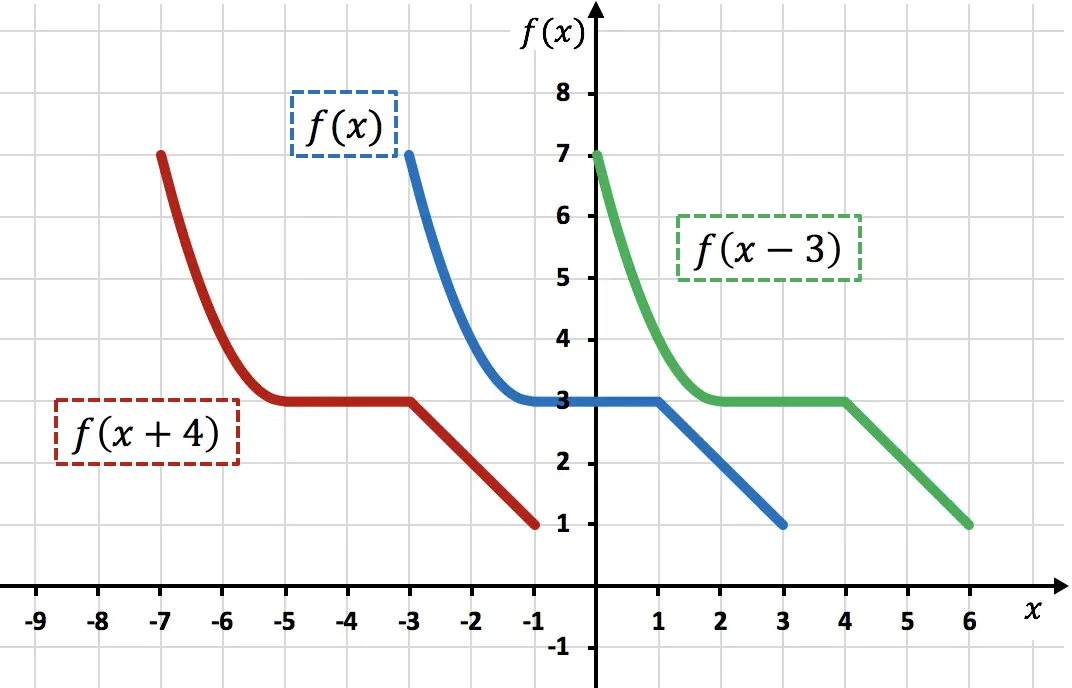
Seperti yang Anda lihat dari grafik, saat menambahkan konstanta langsung ke variabel x , fungsi tersebut menggeser unit yang ditambahkan ke kiri (fungsi merah). Sebaliknya, saat mengurangkan suatu bilangan dari variabel x , fungsinya akan menggeser satuan yang dikurangi ke kanan (fungsi hijau).
Perhatikan bahwa pada jenis pergerakan ini, hanya koordinat X dari titik fungsi yang diubah, sedangkan koordinat Y tetap dengan nilai yang sama.
Contoh menerjemahkan atau memindahkan suatu fungsi
- Pindahkan fungsi berikut 4 satuan ke atas dan 3 satuan ke kanan:
![]()
Untuk menaikkan fungsi tersebut sebanyak 4 satuan, kita perlu menambahkan 4 satuan pada fungsi tersebut:
![]()
Dan untuk juga memindahkan fungsi tersebut sebanyak 3 satuan ke kanan kita harus menghitungnya
![]()
. Oleh karena itu, dimana terdapat a
![]()
kita dapat
![]()
![]()
Fungsinya bergeser 4 satuan ke atas dan 3 satuan ke kanan adalah:
![]()
Di bawah ini Anda memiliki grafik fungsi asli dan fungsi yang diubah sehingga Anda dapat melihat perbedaan di antara keduanya:
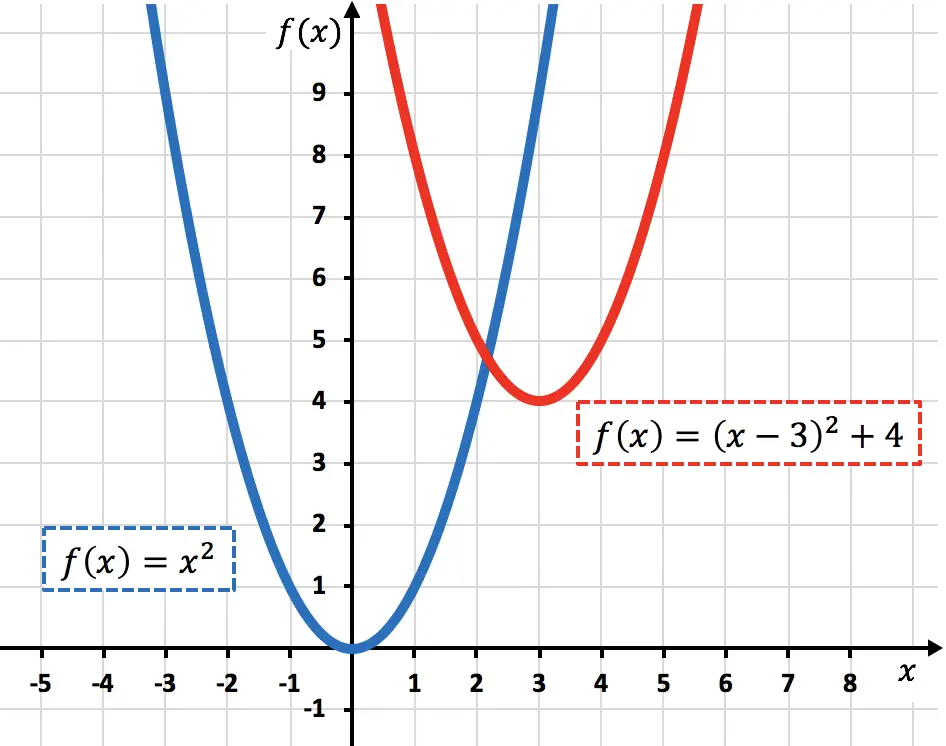
Beberapa ahli matematika menyebut perpindahan miring atau translasi ketika kedua jenis gerak terjadi pada waktu yang bersamaan.
Refleksi atau simetri suatu fungsi terhadap sumbu koordinat
Kita dapat merepresentasikan fungsi simetris terhadap sembarang sumbu kartesius dengan cara berikut:
Untuk merefleksikan suatu fungsi terhadap sumbu x, kita perlu mengubah tanda fungsi tersebut, yaitu kita perlu menghitung
![]()
Untuk merefleksikan suatu fungsi terhadap sumbu y, kita harus meniadakan variabel bebas x , yaitu kita harus menghitung
![]()

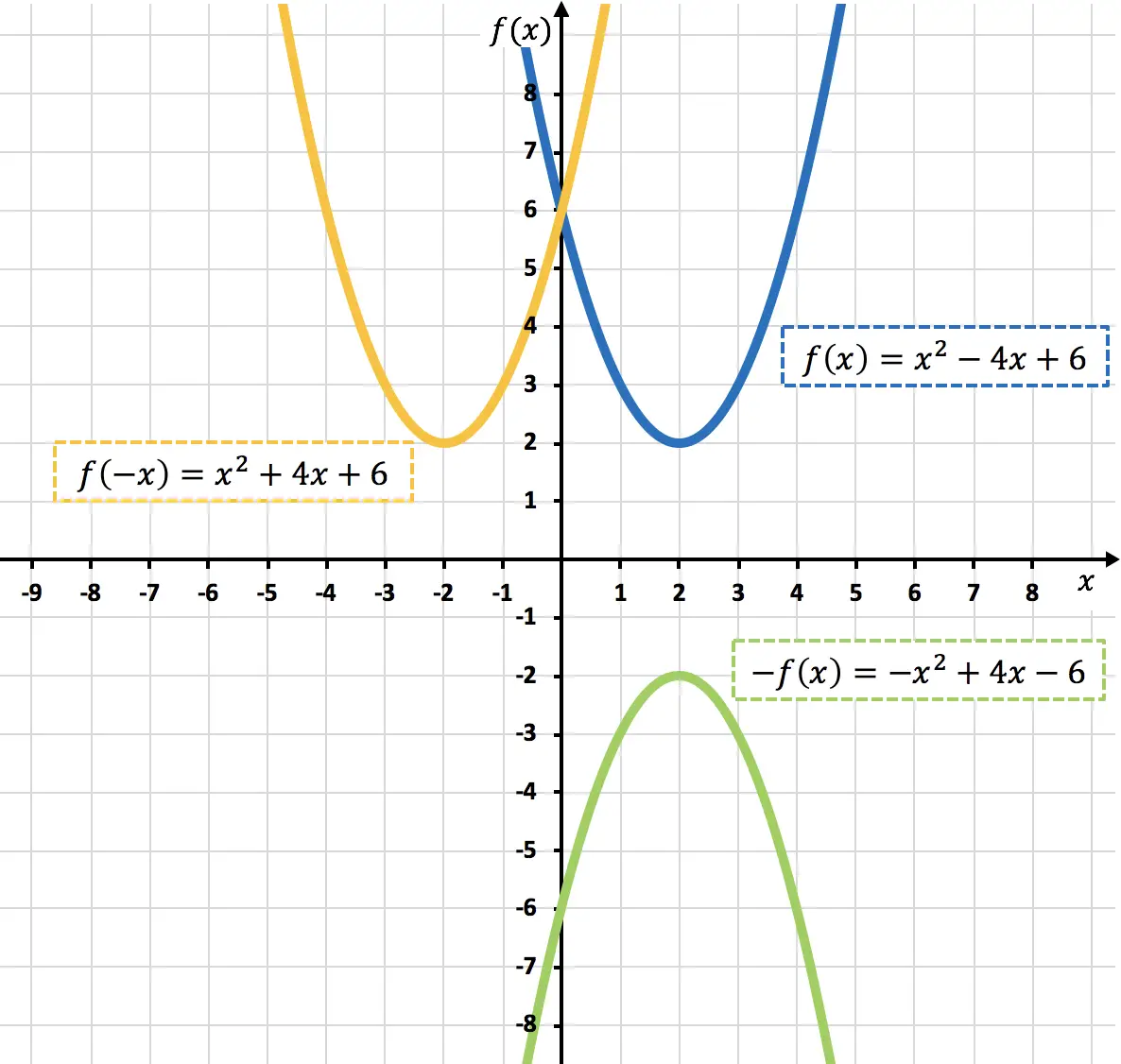
Seperti yang Anda lihat pada grafik sebelumnya, dengan mengalikan suatu fungsi dengan -1, kita membalikkannya secara grafis (fungsi oranye), atau dengan kata lain, kita mencerminkannya relatif terhadap sumbu X.
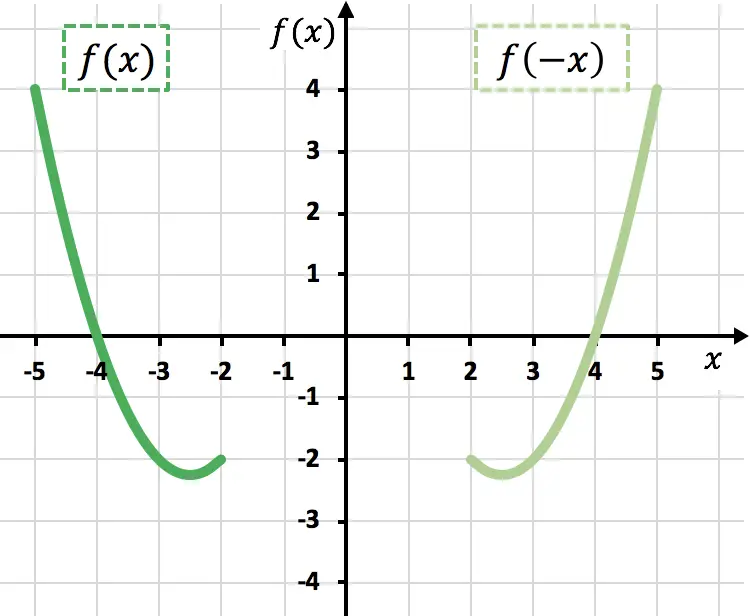
Seperti dapat dilihat pada grafik sebelumnya, dengan meniadakan variabel x , kita mencerminkan fungsi tersebut terhadap sumbu Y (fungsi hijau muda).
Contoh mencerminkan suatu fungsi
- Hitung fungsi simetris terhadap sumbu OX dan fungsi simetris terhadap sumbu OY dari fungsi kuadrat berikut:
![]()
Untuk mencari fungsi yang simetris terhadap sumbu X, kita harus melakukannya
![]()
:
![]()
![]()
Dan untuk mencari fungsi yang simetris terhadap sumbu Y harus kita lakukan
![]()
. Oleh karena itu, kami mengganti jika ada a
![]()
dalam fungsi aslinya dengan istilah tersebut
![]()
![]()
![]()
![]()
![]()
Di bawah ini Anda telah mewakili fungsi asli dan fungsi simetris yang ditemukan:
Fungsi ekspansi dan kontraksi
Seperti halnya terjemahan, ada dua jenis perluasan atau kontraksi: vertikal dan horizontal.
Ekspansi dan kontraksi vertikal suatu fungsi
Dengan mengalikan fungsi bilangan bulat dengan koefisien, kita dapat membuatnya mengembang atau menyusut:
Untuk memperluas (atau melebarkan) suatu fungsi pada sumbu Y, kita perlu mengalikannya dengan angka yang lebih besar dari 1:
 Untuk mereduksi suatu fungsi pada sumbu Y, kita perlu mengalikannya dengan bilangan positif yang kurang dari 1:
Untuk mereduksi suatu fungsi pada sumbu Y, kita perlu mengalikannya dengan bilangan positif yang kurang dari 1:
 Untuk mereduksi fungsi pada sumbu X, kita perlu mengalikan semua x dengan angka yang lebih besar dari 1:
Untuk mereduksi fungsi pada sumbu X, kita perlu mengalikan semua x dengan angka yang lebih besar dari 1:

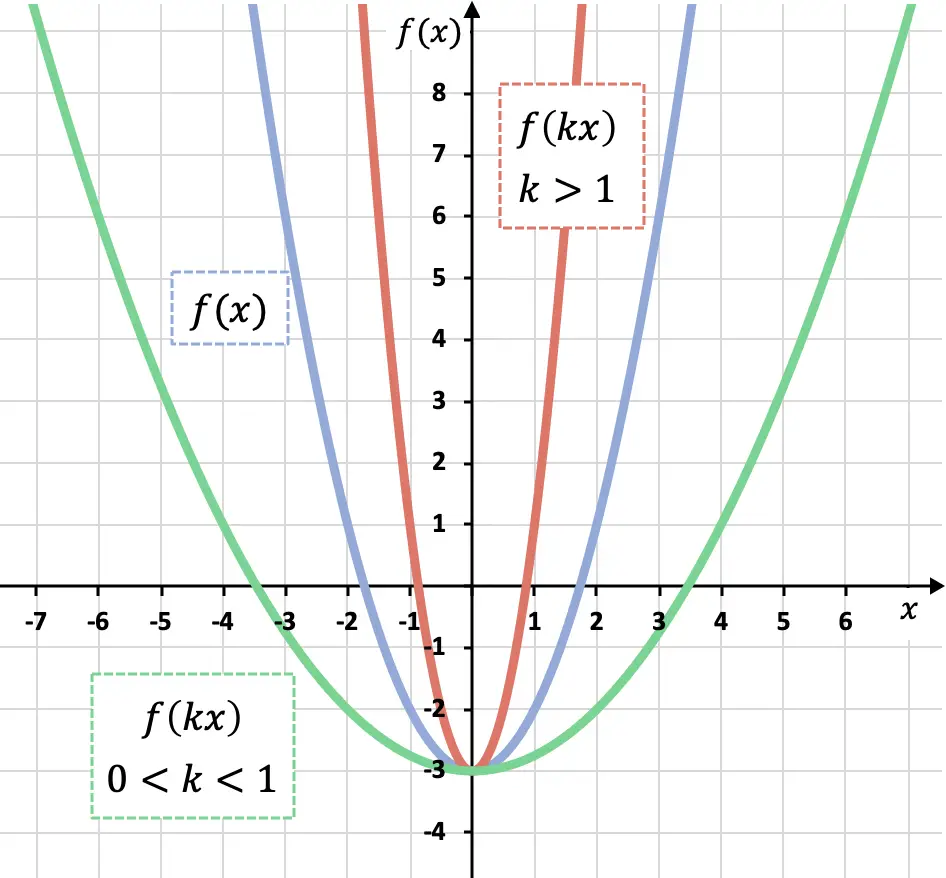
Seperti yang Anda lihat pada grafik sebelumnya, jika kita mengalikan semua x suatu fungsi dengan koefisien yang lebih besar dari 0 tetapi kurang dari 1 (fungsi hijau), kita memperbesarnya sepanjang sumbu OX, sebaliknya jika kita mengalikannya fungsi dengan koefisien lebih besar dari 1 (fungsi merah) kita kurangi sepanjang sumbu OX.
Contoh cara memperluas atau menciutkan suatu fungsi
- Gandakan fungsi irasional berikut secara vertikal dan horizontal:
![]()
Untuk memperluas fungsi pada sumbu y dengan dua, kita harus mengalikan seluruh fungsi dengan 2:
![]()
Dan untuk memperluas fungsi tersebut dengan dua pada sumbu x, kita harus mengalikan semua x dari fungsi tersebut dengan
![]()
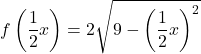
Oleh karena itu, fungsi yang diduplikasi pada dua sumbu koordinat adalah:
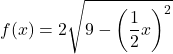
Di bawah ini Anda memiliki fungsi asli dan fungsi yang diubah direpresentasikan secara grafis sehingga Anda dapat melihat perbedaan di antara keduanya:
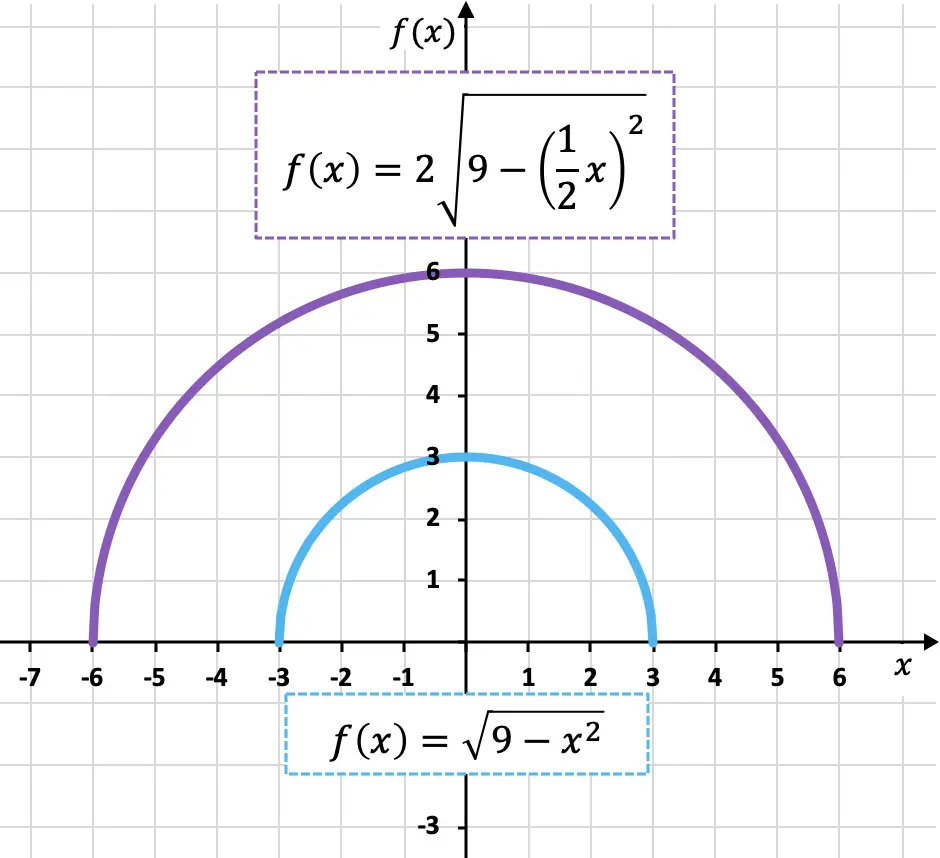
Seperti yang Anda lihat, fitur baru (warna ungu) berukuran dua kali lebih besar dari fitur asli (warna biru) baik secara vertikal maupun horizontal, oleh karena itu fitur tersebut diperluas.
Latihan soal transformasi fungsi
Latihan 1
Pindahkan fungsi derajat ketiga berikut ini ke atas sebanyak 5 satuan:
![]()
Untuk menaikkan fungsi sebanyak 5 satuan, tambahkan 5 ke fungsi tersebut:
![Rendered by QuickLaTeX.com \begin{aligned} f(x) + 5 & = 4x^3-9x-2 + 5 \\[2ex] & = 4x^3-9x+3 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d29d1537293d975f7fbda8871622660f_l3.png)
Maka fungsi yang digeser sebanyak 5 satuan adalah:
![]()
Latihan 2
Temukan fungsi simetris terhadap sumbu Y dari fungsi kuadrat berikut:
![]()
Untuk mencari fungsi yang simetris terhadap sumbu Y perlu dilakukan perhitungan
![]()
, artinya, kita perlu menggantinya
![]()
Untuk
![]()
dalam fungsi:
![]()
![]()
Oleh karena itu, fungsi simetris terhadap sumbu OY adalah:
![]()
Latihan 3
Lakukan kompresi horizontal fungsi berikut hingga sepertiga representasinya:
![]()
Untuk mengurangi suatu fungsi melalui
![]()
![]()
![]()
Oleh karena itu, fungsi tereduksinya adalah:
![]()
Latihan 4
Hitung fungsi simetris terhadap sumbu OX dari fungsi berikut yang diterjemahkan 4 satuan ke kanan:
![]()
Sebelum menghitung fungsi simetris, terlebih dahulu kita harus memindahkan fungsi tersebut 4 satuan ke kanan, maka:
![]()
![]()
![]()
Dan setelah kita memindahkan fungsinya, kita menghitung fungsi simetris terhadap sumbu X. Untuk melakukan ini, kita harus meniadakan fungsi yang diperoleh:
![]()
![]()
Singkatnya, fungsi setelah menerapkan semua operasi dasar adalah:
![]()
Latihan 5
Geser fungsi berikut 2 satuan ke kiri, lalu perluas secara vertikal sebanyak 4 kali:
![]()
Pertama, kita pindahkan fungsinya dua satuan ke kiri:
![]()
![]()
![]()
Dan kemudian kita perluas fungsinya sepanjang sumbu Y dengan faktor 4:
![]()
![]()
Kesimpulannya, fungsi setelah menerapkan semua transformasi dasar adalah:
![]()
Latihan 6
Dari fungsinya
![]()
tentukan representasi mana pada grafik yang sesuai dengan fungsi tersebut
![]()
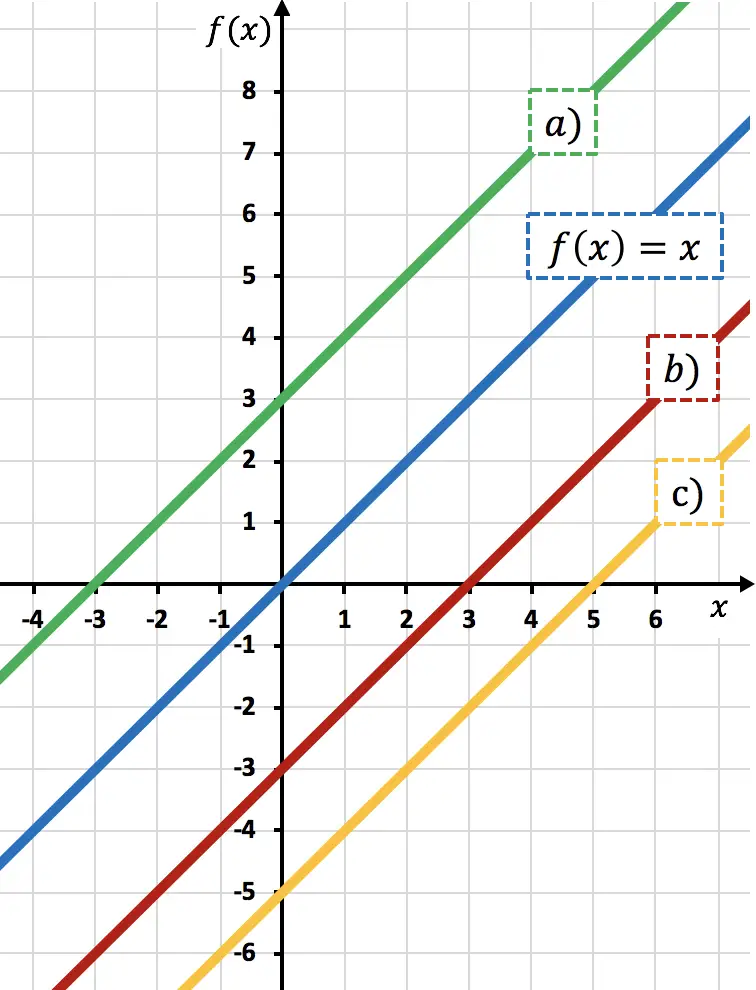
Fungsi
![]()
adalah fungsinya
![]()
turun 3 unit. Karena dengan mengurangkan suatu bilangan dari suatu fungsi, Anda menurunkan fungsi tersebut.
Oleh karena itu, representasi dari
![]()
sesuai dengan garis b) , karena digeser ke bawah sebanyak 3 satuan dibandingkan dengan
![]()
Hal ini dapat dilihat dengan melihat sumbu vertikal: kapan
![]()
melewati 0, garis merah melewati -3, sehingga digeser ke bawah 3 satuan.
Latihan 7
Dari fungsinya
![]()
tentukan parabola mana yang merupakan representasi fungsi tersebut
![]()
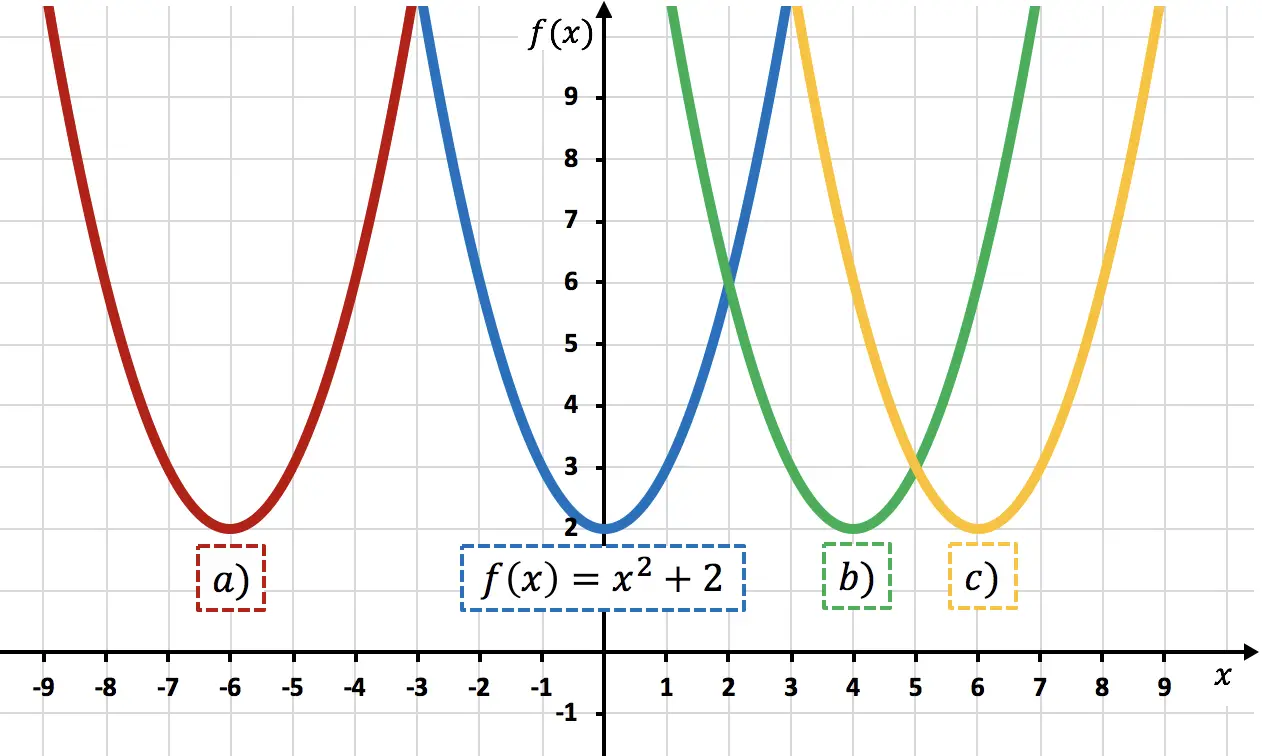
Fungsi
![]()
adalah fungsinya
![]()
berpindah 6 unit ke kanan. Kita dapat memverifikasi ini dengan menghitung
![]()
![]()
![]()
Oleh karena itu, representasi dari
![]()
sesuai dengan parabola c) , karena digeser 6 satuan ke kanan dibandingkan dengan
![]()
.
Hal ini dapat dilihat dengan melihat titik sudut parabola: jarak antara titik sudut parabola
![]()
dan titik puncak parabola c) berjumlah 6 satuan, maka titik puncak parabola c) digeser ke kanan sebanyak 6 satuan dibandingkan yang pertama.