Perbandingan trigonometri suatu sudut adalah perbandingan yang diperoleh dari ketiga sisi suatu segitiga siku-siku. Dengan kata lain, ini adalah nilai yang dihasilkan dari perbandingan ketiga sisinya dengan menggunakan hasil bagi (pembagian). Meskipun perlu diperhatikan bahwa alasan tersebut hanya ada pada segitiga siku-siku (segitiga yang sudutnya 90º).
Perbandingan trigonometri pada segitiga siku-siku
Enam perbandingan trigonometri yang paling penting adalah: sinus, kosinus, tangen, kosekan, garis potong, dan kotangen. Selanjutnya, kami akan menjelaskan secara rinci bagaimana masing-masing alasan ini didefinisikan dan kami akan membahas rumus yang menjadi cirinya. Untuk memahami penjelasan berikut ini kita akan memperhatikan segitiga siku-siku berikut ini:

Dada
Sinus suatu sudut (sin atau sin) sama dengan hasil bagi kaki yang berhadapan (a) antara sisi miring (c), maka rumus sinusnya adalah: sin (α) = a / c . Sangat penting untuk mengetahui definisi sinus ini, karena ini adalah dasar dari semua trigonometri, beserta alasan lainnya yang akan kita bahas di bagian ini.
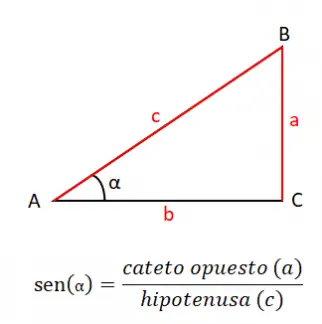
Trav Dari teorema sinus, kita dapat menghitung sisi mana pun dari segitiga , kita dapat melakukannya dengan menghubungkan hasil bagi suatu sudut tertentu antara sisi-sisi yang bersesuaian. Misalnya kita ingin menghitung sisi a dan kita mempunyai nilai sisi sudut A dan B, kita dapat melakukannya dengan menggunakan rumus: a / sin (A) = b / sin (B) . Dengan menyelesaikan persamaan sederhana ini, kita memperoleh nilai yang sesuai dengan variabel yang ingin kita hitung.
Kosinus
Kosinus suatu sudut (cos) sama dengan hasil bagi kaki yang berdekatan (b) antara sisi miring (c), sehingga rumus kosinusnya adalah: cos (α) = b / c . Dalam hal ini rumusnya terdiri dari dua sisi segitiga yang bersentuhan dengan sudut yang ingin kita pelajari, dalam contoh ini sudut A atau α.
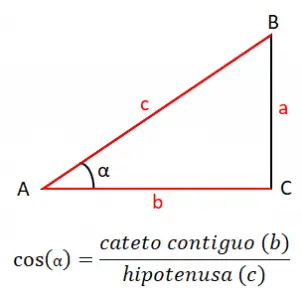
Dengan kosinus, kita juga punya cara menghitung sisi-sisi segitiga , yang berasal dari teorema kosinus. Hal ini memungkinkan kita untuk menghubungkan sisi ke sudut dan memberi kita tiga ekspresi berikut:
a² = b² + c² – 2bc cos (A)
b² = a² + c² – 2ac cos (B)
c² = a² + b² – 2ab cos (C)
Garis singgung
Alasan terpenting ketiga, yang dengannya kita akan menutup rangkaian alasan awal, adalah garis singgung (tan atau tg). Dihitung dengan membagi antara kaki yang berhadapan (a) dan kaki yang bersebelahan (b), maka rumus tangennya adalah: tan (α) = a / b . Anda dapat melihatnya secara grafis di bawah ini:
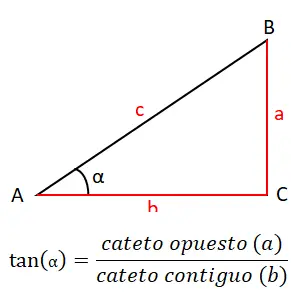
Garis singgung juga mempunyai teorema tersendiri yang disebut teorema tangen. Hal ini memungkinkan kita untuk menghubungkan panjang dua sisi segitiga dengan garis singgung sudutnya . Pernyataannya sebagai berikut: “hasil bagi jumlah dua sisi yang dikurangi sama dengan hasil bagi antara garis singgung rata-rata dua sudut yang berhadapan dengan sisi-sisi tersebut dan garis singgung setengah selisih kedua sudut tersebut”.
Rasio trigonometri yang diturunkan
Dari ketiga perbandingan trigonometri yang baru saja kita bahas, kita dapat memperoleh turunan perbandingan trigonometri lainnya. Ini diperoleh dengan mengambil rasio terbalik terhadap sinus, kosinus dan tangen.
- Cosecant: merupakan perbandingan kebalikan dari sinus dan dihitung dengan rumus: cosec (α) = c / a dan cosec (α) = 1 / sin (α).
- Garis potong: merupakan perbandingan kebalikan dari cosinus dan dihitung dengan rumus: sec (α) = c / b dan sec (α) = 1 / cos (α).
- Kotangen : merupakan perbandingan kebalikan dari garis singgung dan dihitung dengan rumus: cotg (α) = b / a dan cotg (α) = 1 / tan (α).
Tabel perbandingan trigonometri
Di bawah ini Anda dapat melihat tabel yang merangkum semua alasan yang telah dijelaskan sejauh ini. Dengan tabel ini Anda akan dapat menghafal semua rumus secara efektif, karena memungkinkan Anda dengan mudah membedakan perbedaan setiap ekspresi matematika.
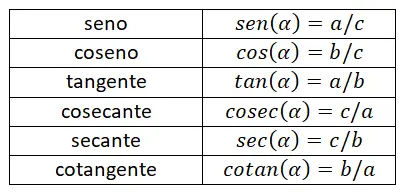
Perbandingan trigonometri dalam lingkaran
Cara lain untuk mempelajari trigonometri adalah melalui keliling goniometri atau lingkaran satuan , keliling ini mempunyai jari-jari sama dengan 1 dan titik asal adalah titik (0, 0). Gambarnya terdiri dari lingkaran dan segitiga siku-siku yang digambarkan di dalam lingkaran, lebih tepatnya sudut yang akan kita pelajari harus menyentuh titik semula.
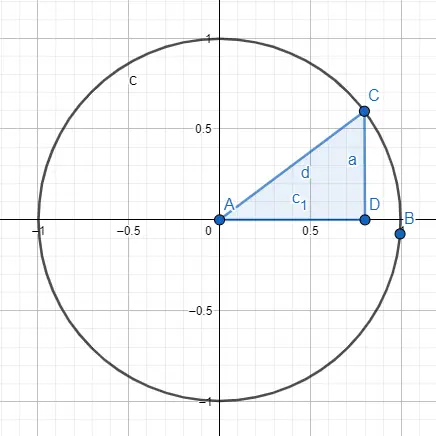
Jika kita mempunyai gambar ini, kita mengetahui bahwa jari-jarinya sama dengan sisi miringnya, yaitu sama dengan 1. Jadi jika kita ingin menghitung sinus dan cosinusnya, kita akan menggunakan nilai jari-jari dan nilai sisi lain dari gambar tersebut. segitiga. Untuk menghitung sinus, kita lakukan perhitungan sebagai berikut: sin (A) = CD / AC = CD / radius = CD / 1 = CD , jadi sinus dari A adalah a. Sedangkan untuk menghitung cosinus kita akan melakukan perhitungan: cos (A) = AD / AC = AD / radius = AD / 1 = AD , maka cosinus dari A adalah c1.
Sangat penting untuk mengingat dua hal. Yang pertama adalah penggunaan lingkaran ini dalam studi perbandingan trigonometri karena adanya kebutuhan untuk menangani sudut yang lebih besar dari sudut yang dapat dipelajari dengan segitiga. Misalnya sudut 150º tidak dapat dipelajari melalui segitiga sederhana, karena terlalu besar. Dan hal kedua yang perlu diingat adalah sinus dan cosinus tidak pernah bisa mengambil nilai lebih besar dari 1 dan kurang dari -1.
Tanda perbandingan trigonometri
Seperti yang telah kami katakan sebelumnya, untuk menangani sudut yang lebih besar dari yang dapat ditangani oleh segitiga, kami menggunakan keliling goniometri. Untuk melakukan ini kita mewakili sebuah segitiga di dalam lingkaran tepat di salah satu dari empat kuadran yang membagi keliling, pada gambar berikut Anda dapat melihat empat kuadran yang diwakili.
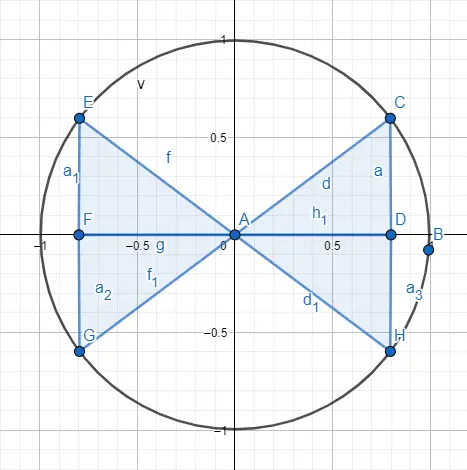
Nah, untuk membedakan sudut 30 dan salah satu sudut 210, yang menjadi sama mengenai distribusi di dalam segitiga , kita akan menggunakan sebaran tanda menurut kuadran dimana segitiga itu berada. Di bawah ini Anda dapat melihat tanda-tanda yang sesuai dengan setiap kuadran dan contoh yang digambar.
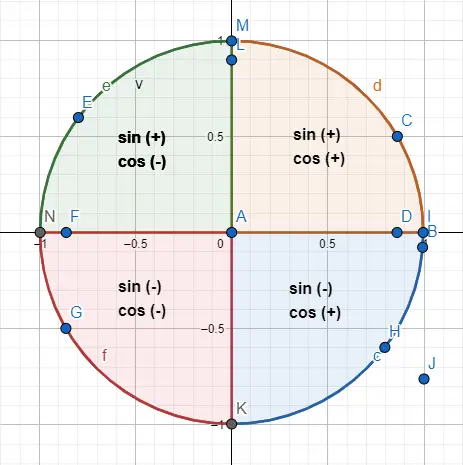
Misalnya, sudut 30º dan 210º mempunyai nilai numerik yang sama , tetapi sinus dan cosinusnya mempunyai tanda yang berlawanan. Jadi: sin(30) = 1/2 dan cos(30) = √3/2, sedangkan sin(210) = -1/2 dan cos(210) = -√3/2. Untuk mencapai hasil ini kami mewakili dua sudut pada keliling (gambar di bawah) dan kami mengikuti indikasi tandanya.
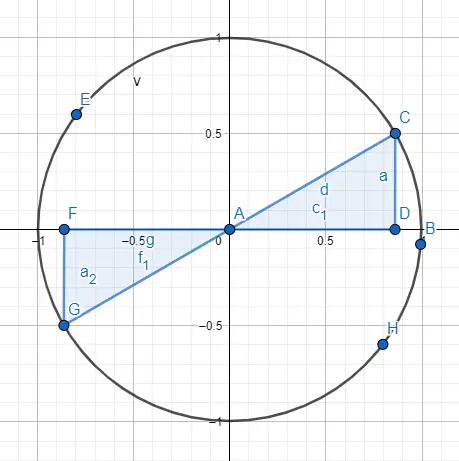
Terakhir, bagaimana mungkin sudutnya lebih besar dari 360º , meskipun kelihatannya tidak seperti itu karena kelilingnya hanya 360º. Namun, jika kita ingin mencari sudut 750º, kita bisa menguranginya menjadi sudut antara 0º dan 360º. Cukup kita bagi 750 dengan 360 dan sisanya adalah sudut yang tersisa, dalam kasus 750º kita mendapatkan sudut 30º.
Jenis sudut tergantung pada kuadrannya
Ada hubungan antara sudut yang berbeda, yang memungkinkan kita menghitung rasionya nilai trigonometri semua sudut yang termasuk dalam lingkaran. Mari kita cari tahu alasannya pengurangan ke kuadran pertama . Artinya kita membuat penyederhanaan dari sudut tertentu ke kuadran pertama lalu menerapkan tanda-tanda yang sesuai. Di bawah ini Anda akan menemukan berbagai prosedur yang dijelaskan (tergantung pada kuadran):
kuadran pertama
Pada kuadran pertama ini (0º – 90º), kita hanya perlu menyelesaikan perbandingan trigonometri dengan sudut yang diberikan. Dan jika kita lihat pada gambar yang telah kita jelaskan sebelumnya tentang simbol, sinus dan cosinus mempunyai nilai positif di depannya (hasil yang kita peroleh tidak akan terpengaruh oleh tanda).
Pengurangan dari kuadran kedua ke kuadran pertama
Pada kuadran kedua (90º – 180º) kita berhadapan dengan sudut bersuplemen, artinya kedua sudut tersebut berjumlah 180º. Oleh karena itu, kita perlu melakukan pengurangan dari kuadran kedua ke kuadran pertama dan kita lakukan dengan rumus 180 – α = β , dimana α adalah sudut kuadran pertama dan β adalah sudut asal.
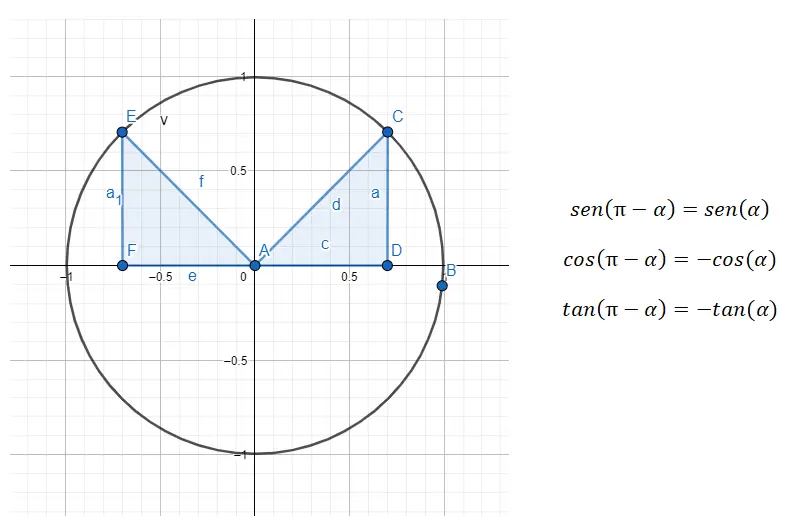
Misalnya, jika kita diberi sudut 135º (termasuk kuadran kedua), kita perlu mencari sudut dari kuadran pertama yang berhubungan dengan kuadran pertama. Pada contoh ini, sudut (α) yang kita cari adalah 45º, karena 180 – 45 = 135. Jadi, benar: sin (135) = sin (180 – 45) = sin (45), cos (135 ) = cos (180 – 45) = -cos (45) dan tan (135) = tan (180 – 45) = -tan (45).
Pengurangan kuadran ketiga menjadi kuadran pertama
Pada kuadran ketiga (180º – 270º) , kita berhadapan dengan sudut-sudut yang berbeda sebesar 80º, artinya jarak kedua sudut tersebut adalah 180º. Jadi jika kita ingin mengurangi dari kuadran ketiga ke kuadran pertama, kita perlu menggunakan rumus 180 + α = β , dimana α adalah sudut kuadran pertama dan β adalah sudut aslinya.
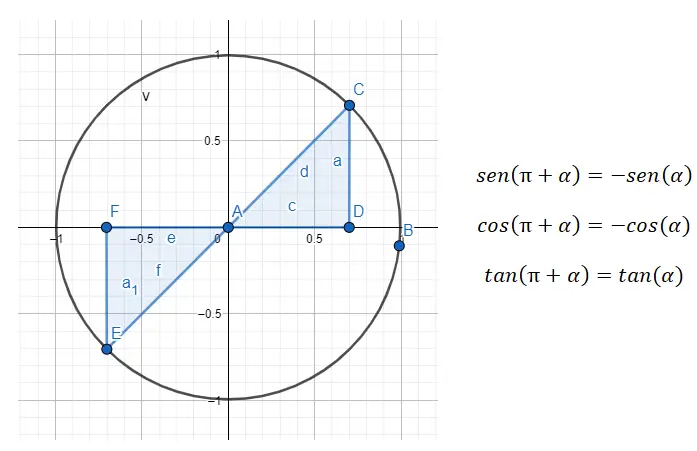
Misalnya, jika kita diberi sudut 225º (yang termasuk dalam kuadran ketiga), kita perlu mencari sudut kuadran pertama yang sesuai dengan sudut tersebut. Dalam kasus 225º, sudut (α) yang kita cari adalah 45º lagi, karena 180 + 45 = 225. Jadi, sin (225) = sin (180 + 45) = -sin (45), cos (225) = cos (180 + 45) = -cos (45) dan tan (225) = tan (180 + 45) = tan (45) terpenuhi. ).
Pengurangan kuadran keempat menjadi kuadran pertama
Di kuadran keempat (270º – 360º) kita berhadapan dengan sudut yang berlawanan, yang berarti sudut-sudutnya sama besar, tetapi berlawanan tanda , seperti 30º dan -30º (setara dengan 330º, karena 360º – 30º = 330º) . Penting untuk diingat bahwa sudut yang berhadapan dapat ditulis sebagai sudut positif dan sudut negatif atau sebagai dua sudut positif (pada contoh yang baru saja kita bahas, kami telah menjelaskan perbedaannya).
Jadi jika kita ingin melakukan pengurangan dari kuadran keempat ke kuadran pertama, kita perlu menggunakan rumus 360 – α = β , dimana α adalah sudut kuadran pertama dan β adalah sudut asal.
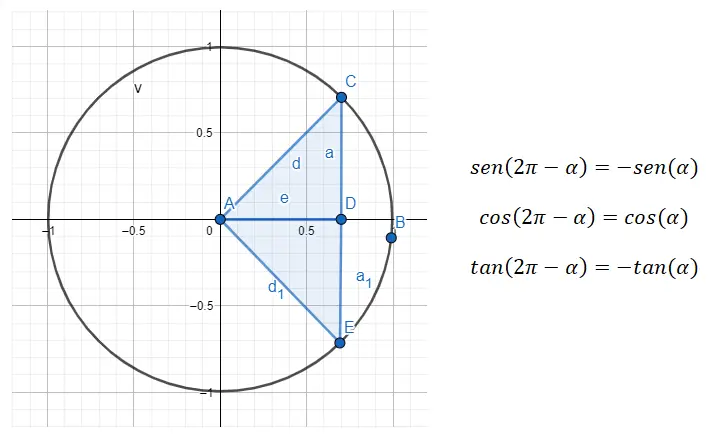
Misalnya, jika kita diberi sudut 315º (termasuk kuadran keempat), kita perlu mencari sudut kuadran pertama yang berhubungan dengan kuadran pertama. Kalau sudut (α) yang kita cari masih 45º, karena 360 – 45 = 315. Jadi sin (315) = sin (360 – 45) = -sin (45), cos ( 315 ) = cos (360 – 45) = cos (45) dan tan (315) = tan (360 – 45) = -tan (45). Kesimpulannya, kita telah melihat sudut yang berasal dari 45º dari semua kuadran.
Perbandingan trigonometri sudut terpenting
Ada sejumlah sudut, yang disebut sudut penting , yang paling umum digunakan dalam trigonometri. Mengetahui rasio trigonometri Anda dengan hati sangat dianjurkan. Oleh karena itu, di bawah ini kami telah membuat tabel yang berisi perbandingan trigonometri sudut-sudut tersebut dan turunannya (sudut yang sama, tetapi dengan perbedaan 90, 180 atau 270 derajat):
| Sudut (°) | Sudut (rad) | Dada | Kosinus | Garis singgung |
| 0º | 0 rad | 0 | 1 | 0 |
| 30º | 1/6 rad | 1/2 | √3/2 | √3/3 |
| 45º | 1/4 rad | √2/2 | √2/2 | 1 |
| 60º | 1/3 rad | √3/2 | 1/2 | √3 |
| 90º | 1/2πrad | 1 | 0 | ∞ |
| 120º | 5/8πrad | √3/2 | -1/2 | -√3 |
| 135º | 3/4 rad | √2/2 | -√2/2 | -1 |
| 150º | 5/8πrad | 1/2 | -√3/2 | -√3/3 |
| 180º | πrad | 0 | -1 | 0 |
| 225º | 5/4 rad | -√2/2 | -√2/2 | 1 |
| 270º | 3/2πrad | -1 | 0 | ∞ |
| 315º | 7/4 rad | -√2/2 | √2/2 | -1 |
Hubungan antara perbandingan trigonometri
Ada beberapa cara untuk menghubungkan berbagai perbandingan trigonometri. Dari hubungan tersebut kita memperoleh semacam persamaan antara berbagai fungsi trigonometri, yang kita sebut identitas trigonometri. Berkat jenis identitas ini kami dapat menghitung rasio berdasarkan identitas lainnya. Perlu diperhatikan bahwa ada banyak jenis identitas trigonometri, yang diklasifikasikan berdasarkan jenis hubungan yang mendukung ekspresi itu sendiri.
Rasio Trigonometri Soal Terpecahkan
Selanjutnya, kami menawarkan kepada Anda serangkaian latihan yang dapat Anda gunakan untuk mempraktikkan semua teori yang dijelaskan dalam artikel ini. Ingatlah bahwa jika suatu saat Anda mengalami kebuntuan atau memiliki pertanyaan, Anda dapat membaca ulang artikel tersebut dan tentunya, dengan membaca kedua kali , Anda akan memahami segalanya dengan lebih baik. Meskipun demikian, Anda dapat mulai berlatih:
Latihan 1
Hitung enam perbandingan trigonometri sudut 225º:
Kita mulai dengan menghitung sudut (α) yang sama dengan: 180 + α = 225º, maka α = 45º.
sin(225) = sin(180 + 45) = -sin(45) = -√2/2
cos(225) = cos(180 + 45) = -cos(45) = -√2/2
tan(225) = tan(180 + 45) = tan(45) = 1
Latihan 2
Hitung enam perbandingan trigonometri sudut 120º:
Kita mulai dengan menghitung sudut (α) yang sama dengan: 180 – α = 120º, maka α = 60º.
dosa(120) = dosa(180 – 60) = dosa(60) = √3/2
cos(120) = cos(180 – 60) = -cos(60) = -1/2
tan(120) = tan(180 – 60) = -tan(60) = -√3
Latihan 3
Hitung enam perbandingan trigonometri sudut 510º:
Sebelum memulai, Anda harus melakukan pengurangan sudut: 510/360 = 1 putaran dan sisa sudut 150. Selanjutnya kita hitung sudut (α) yang sama dengan: 180 – α = 150, maka α = 30º.
dosa(150) = dosa(180 – 30) = dosa(30) = 1/2
cos(150) = cos(180 – 30) = -cos(30) = -√3/2
tan(150) = tan(180 – 30) = -tan(30) = -√3/3