Kotak Ajaib adalah permainan puzzle matematika yang melatih kemampuan berhitung kita dengan cara yang menyenangkan dan mengasyikkan. Itulah mengapa ini adalah salah satu sumber terbaik untuk mengajarkan matematika kepada siswa muda.
Apa itu array ajaib dan bagaimana cara mengatasinya?
Kotak ajaib adalah sejenis tabel atau matriks yang terdiri dari kotak-kotak berbeda, yang di dalamnya ditulis bilangan bulat . Namun, dalam keadaan apa pun mereka tidak dapat dipasang; serangkaian aturan harus dihormati:
- Semua jumlah ajaib (jumlah semua nilai garis horizontal, vertikal, atau diagonal) harus selalu memberikan nilai yang setara dengan konstanta ajaib (itu adalah nilai tunggal).
- Tidak ada angka yang dapat diulang dua kali.
- Anda hanya dapat menggunakan angka berurutan (misalnya 1 sampai 9) atau angka yang mengikuti deret tertentu, misalnya: angka ganjil, kelipatan 5, dan lain-lain.
Selain itu, penting untuk ditekankan bahwa kita dapat membuat klasifikasi persegi yang berbeda-beda bergantung pada strukturnya. Yang pertama menurut derajat persegi , yaitu setara dengan jumlah sel yang ada dalam satu baris atau kolom. Dan yang kedua sesuai dengan jenis derajat tabelnya ( bilangan genap atau bilangan ganjil). Dari perbedaan ini kita dapat mengatur semua kotak ke dalam kategori yang berbeda, walaupun kita akan merincinya nanti.
Bagaimana cara menyelesaikan kotak ajaib?
Untuk menyelesaikan permainan matematika ini, kita dapat menggunakan dua metode berbeda: menggunakan geometri atau menghitung konstanta ajaib. Kedua prosedur tersebut sama-sama valid, meskipun prosedur yang satu memungkinkan Anda mencapai hasil lebih cepat, sedangkan prosedur lainnya memerlukan lebih banyak waktu dan alasan . Selanjutnya kami akan menjelaskan kedua metode tersebut, sehingga Anda dapat memilih salah satu yang Anda sukai dan dapat lebih beradaptasi dengan setiap situasi.
Apa rumus persegi ajaib?
Metode pertama terdiri dari menghitung konstanta ajaib , yang mana kita harus menggunakan rumus berikut: n(n 2 +1)/2, di mana n adalah derajat kuadrat. Dan begitu kita mendapatkan nilai ini, yang tersisa hanyalah mencoba berbagai kombinasi angka, yang memungkinkan kita menyamakan jumlah ajaib seluruh kuadrat dengan konstanta. Dengan kata lain, kita perlu membentuk kombinasi angka-angka yang menjumlahkan nilai konstanta, sehingga gambaran keseluruhannya seimbang.
Bagaimana cara menyelesaikan kotak ajaib menggunakan geometri?
Kedua, kita bisa menyelesaikan kotak ajaib menggunakan geometri . Meskipun perlu dicatat bahwa metode ini sangat sederhana dan tidak mengharuskan Anda melatih keterampilan berhitung, karena ini murni metodis. Oleh karena itu, kami akan menjelaskan prosedur penyelesaian kuadrat genap dan kuadrat ganjil.
Bagaimana cara menyelesaikan kotak ajaib dengan bilangan ganjil?
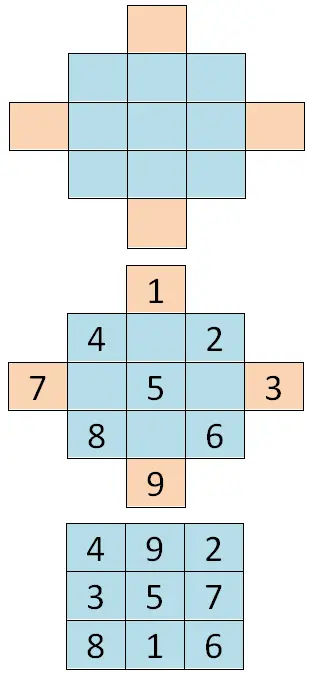
Untuk mengatasi kasus pertama ini, Anda harus menambahkan sel ke tabel awal sehingga memiliki semacam berlian. Kemudian kita harus menulis semua angka berurutan dimulai dengan digit pertama dari rangkaian tersebut (dalam kasus kita 1) dan kita akan mengikuti diagonal berlian . Terakhir, kita perlu “menggandakan” angkanya, sehingga nilai sel terluarnya mengarah ke sisi yang berlawanan. Jadi sel-sel terluar dari sumbu vertikal berpotongan, kemudian hal yang sama terjadi pada sel-sel sumbu horizontal, di bawah ini Anda dapat melihat contohnya:
Bagaimana cara menyelesaikan kotak ajaib yang berorde genap?
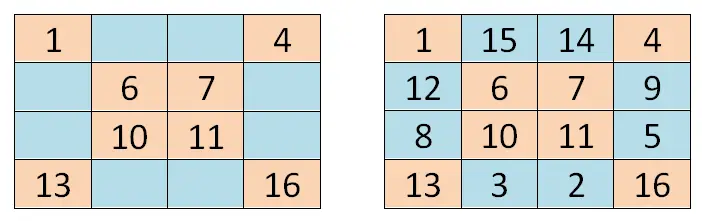
Untuk menyelesaikan persegi ajaib berorde genap (kotak ajaib yang jumlah baris dan kolomnya genap), kita dapat menggunakan metode yang agak berbeda dari metode sebelumnya, tetapi juga didasarkan pada geometri. Kita akan mulai dengan menulis angka pertama dari rangkaian tersebut (dalam kasus kita 1) di sudut kiri atas. Kemudian kita akan melintasi dua diagonal utama dan kita akan menuliskan nilai yang sesuai dengan posisi masing-masing kotak.
Setelah kita menulis dua diagonal utama, kita harus menempatkan diri kita di kotak kosong pertama mulai dari pojok kanan bawah (kotak 15 dalam kasus kita). Di sana kita akan menulis nilai kedua dari rangkaian tersebut dan kita akan menulis nilai yang tersisa secara berurutan (dari terkecil ke terbesar), melengkapi sel dari kanan ke kiri dan dari bawah ke atas . Agar lebih jelas, Anda dapat mengarahkan diri Anda dengan gambar yang kami tunjukkan di bawah ini:
Bagaimana cara membuat kotak ajaib?
Untuk membuat kotak ajaib sendiri, kita dapat mengikuti beberapa prosedur, di antaranya akan kami soroti dua. Perlu dicatat bahwa masing-masing metode akan digunakan untuk membuat kotak dengan tipe berbeda, jadi Anda harus memilih metode dengan hati-hati tergantung pada kotak yang ingin Anda hasilkan:
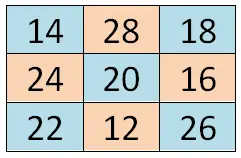
Metode siam
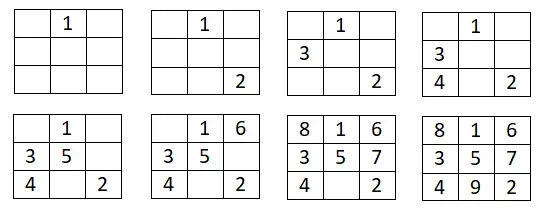
Metode pertama ini cukup sederhana dan secara khusus membantu kita membuat kotak ajaib ganjil dengan ukuran berapa pun. Prosedur yang harus diikuti sangat sederhana, pada dasarnya kita akan menulis bilangan pertama dari rangkaian tersebut di kotak tengah baris pertama. Dari sana, kita akan kembali mengurutkan barisan aritmatika yang telah kita pilih, menulis angka berikutnya ke atas dan ke kanan . Namun, jika posisinya berada di luar kotak yang digambar, kita harus berpindah ke baris atau kolom terakhir. Dan jika kita mendapatkan kotak penuh, kita harus turun satu kotak dari kotak angka terakhir yang kita masukkan dan kemudian kita akan melanjutkan dengan cara yang sama.
Di bawah ini Anda dapat melihat contoh 3×3:
Metode Strachey untuk kotak ajaib
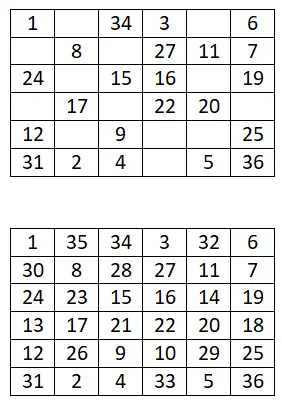
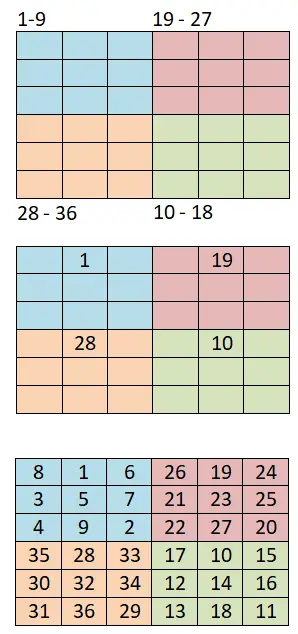
Untuk menghasilkan kotak ajaib berorde 4k + 2 pasang , kita akan menggunakan metode lain ini, yang didasarkan pada metode sebelumnya (metode Siam) dan juga sangat sederhana. Di bawah ini Anda dapat melihat langkah-langkah yang harus diikuti dan contoh kerja persegi ajaib 6×6:
- Membagi menjadi beberapa kuadran yang lebih kecil: Hal pertama yang perlu kita lakukan adalah membagi papan menjadi beberapa kotak yang lebih kecil, misalnya jika kita memiliki papan berukuran 6×6 kita perlu membuat empat kuadran yang sama besar yaitu kotak berukuran 3×3.
- Gunakan metode Siam: maka kita akan menetapkan rentang angka untuk setiap kuadran kecil, misalnya jika kita memulai barisan dengan 1, rentangnya adalah: 1-9 (pertama), 10-18 (keempat), 19-27 (kedua) dan 28-36 (ketiga).
Metode LUX Conway untuk kotak ajaib
Kita akan menggunakan sistem terakhir ketika kita ingin menghasilkan kuadrat ajaib berorde 4n + 2 , di mana n adalah bilangan asli. Jadi, prosedur yang akan kita ikuti untuk membuat kotak dengan gaya ini adalah sebagai berikut:
- Membuat tabel atau matriks: kita akan mulai dengan membuat matriks berderajat 2n + 1, dimana n adalah bilangan asli. Dengan ini kita akan dapat mendesain meja dan memikirkan derajatnya dan kemudian mulai dengan desainnya.
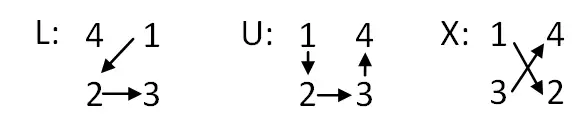
- Penempatan huruf: setelah tabel dibuat, Anda harus menulis dari atas ke bawah: n + 1 baris L, 1 baris U dan n – 1 baris X. Dan kemudian, Anda harus menukar U di tengah dengan huruf L di atas.
- Tukar huruf dengan nilai numerik: Sekarang kita perlu mengganti huruf dengan kelompok empat angka berurutan. Tergantung pada hurufnya, kami akan memberikan satu urutan atau lainnya pada nomor tersebut. Dijelaskan di bawah ini:
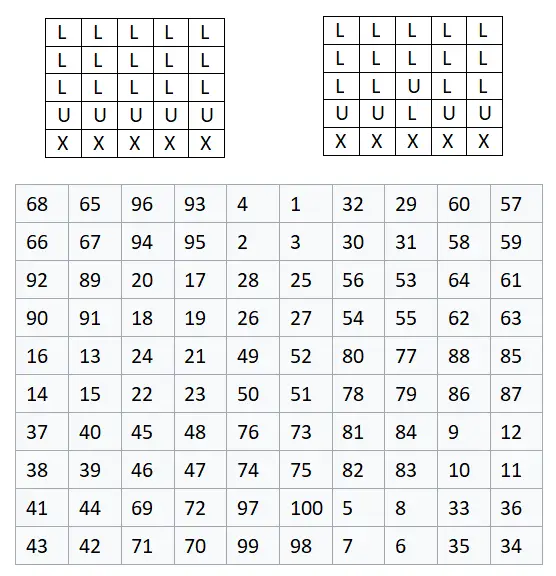
Kita akan mulai dengan membuat matriks berukuran 5×5 , jadi n = 2, karena: 2n + 1 = 2 · 2 + 1 = 5. Artinya matriks tersebut akan berukuran 10×10, karena seperti yang kita lakukan telah kita katakan, setiap sel yang berisi satu huruf setara dengan kelompok empat bilangan, yaitu matriks 2×2. Di bawah ini Anda dapat melihat contoh yang sudah selesai, di mana kami mengganti setiap huruf dengan sekelompok empat angka dalam urutan yang ditunjukkan pada gambar:
latihan kotak ajaib
Selanjutnya, kami menawarkan kepada Anda beberapa kotak ajaib yang tidak lengkap dan Anda harus mengisinya sendiri, berkat konsep yang telah kami jelaskan di artikel ini. Ingatlah bahwa Anda dapat menggunakan salah satu metode yang diajarkan. Selain itu, perlu diingat bahwa 1 mungkin bukan angka pertama dalam rangkaian tersebut, meskipun akan dimasukkan ke dalam deklarasi. Dan ketika Anda menyelesaikan salah satu latihan, Anda akan dapat melihat solusinya di bawah pernyataan tersebut.
persegi ajaib 3×3
Buatlah persegi ajaib 3×3 yang hanya berisi bilangan ganjil:
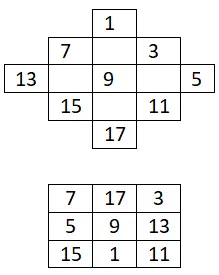
Kotak ajaib 4×4
Selesaikan persegi ajaib 4×4 berikut:
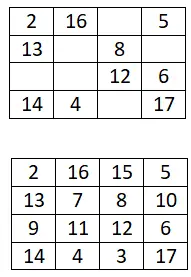
kotak ajaib 5×5
Selesaikan persegi ajaib 5×5 berikut:
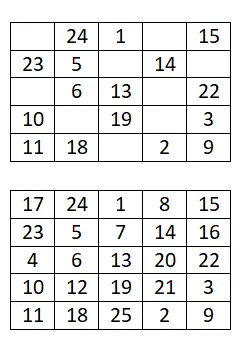
kotak ajaib 6×6
Selesaikan persegi ajaib 6×6 berikut: