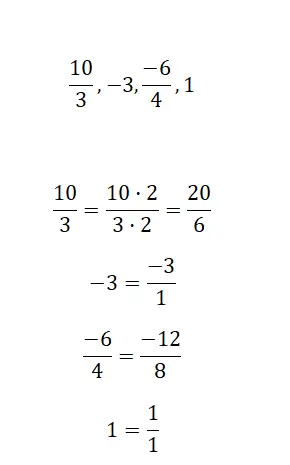Pada artikel ini Anda akan menemukan penjelasan tentang pecahan senilai atau pecahan senilai yang sangat lengkap dan mudah dipahami. Lebih khusus lagi, kita akan membahas tentang definisinya, cara menghitungnya, dan cara mengetahui apakah dua pecahan setara. Dengan cara ini Anda akan mengetahui semua yang Anda perlukan untuk menyelesaikan latihan pecahan senilai seperti yang akan kami sajikan di bagian akhir. Karena itu, mari kita mulai dengan topiknya.
Kalkulator Pecahan Setara
Dengan bantuan kalkulator pecahan senilai ini, Anda akan dapat memeriksa apakah dua pecahan sama, tanpa perlu melakukan perhitungan apa pun. Pengoperasiannya sangat sederhana, pada dasarnya Anda harus memasukkan nilai yang sesuai dengan dua pembilang dan dua penyebut dan tekan tombol “Hitung”.
Apa yang dimaksud dengan pecahan senilai?
Pecahan senilai adalah pecahan yang menyatakan nilai numerik yang sama , oleh karena itu, pecahan tersebut adalah pecahan yang ekuivalen dengan hasil yang sama, meskipun pembilang dan penyebutnya berbeda. Artinya, keduanya mempunyai hubungan proporsional, yang dapat terdiri dari dua jenis: diperkuat atau disederhanakan. Selanjutnya kami tunjukkan contoh grafik pecahan senilai agar konsepnya lebih mudah dipahami.
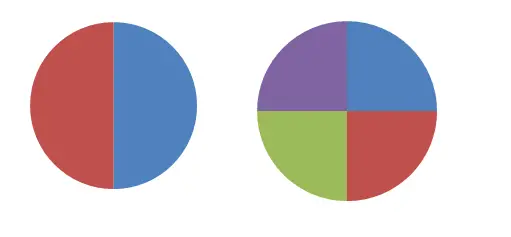
Pada gambar sebelumnya Anda dapat melihat dua lingkaran dibagi menjadi dua dan empat bagian. Jika kita mencoba mendefinisikan bilangan pertama dengan pecahan, kita akan mengatakan bahwa setiap bagian sama dengan 1/2 dari keseluruhan, sedangkan pada gambar kedua kita akan menggunakan pecahan 1/4. Jelasnya, kedua pecahan ini tidak ekuivalen , karena keduanya mewakili besaran yang berbeda. Namun, jika kita mengambil dua buah lingkaran kedua (2/4), persamaan ini setara dengan 1/2.
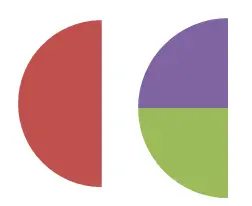
Pada gambar kedua ini Anda dapat melihat kesetaraan antara 1/2 dan 2/4 , juga dapat diverifikasi secara numerik. Karena 1/2 = 0,5 dan 2/4 = 0,5. Berdasarkan definisi yang telah kita bahas sebelumnya, jika kedua pecahan menyatakan nilai numerik yang sama, maka keduanya merupakan pecahan senilai.
Contoh pecahan senilai
Sekarang kami akan menunjukkan kepada Anda 5 contoh pecahan senilai. Dan jika Anda ingin memahami cara kami menghitungnya, kami menyarankan Anda terus membaca.
- Pecahan yang setara dengan setengah: 2/4, 3/6, 4/8, dst.
- Pecahan setara dengan sepertiga: 2/6, 3/9, 4/12, dst.
- Pecahan yang setara dengan seperempat: 2/8, 3/12, 16/4, dst.
- Pecahan yang sama dengan kesatuan: 4/4, 7/7, 15/15, dst.
- Pecahan yang setara dengan seperlima: 2/10, 15/3, 20/4, dst.
Bagaimana cara menghitung pecahan senilai?
Untuk mendapatkan pecahan senilai, kita perlu mengalikan atau membagi pembilang dan penyebutnya dengan angka yang sama. Karena jika kita memodifikasi kedua bagian pecahan dengan cara yang sama, kita mempertahankan hubungan proporsional. Oleh karena itu, kita dapat menggunakan dua metode: amplifikasi dan reduksi.
Menemukan pecahan senilai dengan amplifikasi
Dalam kasus pertama ini, kita perlu mengalikan pecahan awal dengan nilai numerik tertentu. Artinya kita perlu mengalikan pembilang dan penyebutnya dengan bilangan tersebut. Agar Anda dapat melihatnya dengan contoh, di bawah ini kami tunjukkan dua pecahan senilai, yang diperoleh setelah melakukan perkalian:
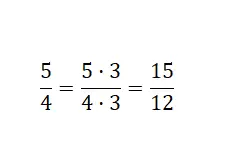
Yang kita lakukan adalah mengalikan kedua bagian pecahan dengan tiga: 5 x 3 = 15 dan 4 x 3 = 12 . Dengan demikian kita memperoleh pecahan ekuivalen yang diperkuat, karena pecahan tersebut lebih besar. Kesimpulannya, kami menemukan pecahan yang terdiri dari nilai numerik berbeda, yang menyatakan besaran yang sama dengan pecahan aslinya.
Mencari pecahan senilai dengan penyederhanaan
Kedua, kita dapat memilih untuk menyederhanakan suatu pecahan dengan membagi pembilang dan penyebut suatu pecahan tertentu. Dengan cara ini kita akan memperoleh pecahan ekuivalen lainnya , bahkan lebih sederhana dari pecahan pertama. Namun, perlu disebutkan bahwa metode ini hanya berfungsi jika ekspresi awalnya bukan pecahan tak tereduksi , karena pecahan tak tereduksi tidak dapat direduksi lebih jauh. Di bawah ini adalah contoh penghitungan pecahan senilai dengan cara reduksi (penyederhanaan).
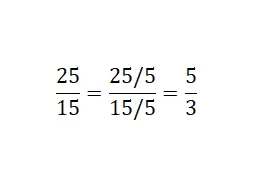
Seperti yang Anda lihat pada gambar, yang kita lakukan adalah membagi pembilang dan penyebut pecahan dengan pembagi persekutuan . Dalam contoh ini, kita menggunakan lima: 25/5 = 5 dan 15/5 = 3. Akhirnya, kita memperoleh pecahan ekuivalen tak tersederhanakan yaitu 25/15.
Bagaimana cara mengetahui dua pecahan setara?
Untuk mengidentifikasi pecahan senilai, kita harus mengikuti salah satu dari tiga prosedur yang akan kami jelaskan di bawah. Perlu diperhatikan bahwa yang kedua terkait dengan penyederhanaan pecahan yang telah kita bahas pada bagian sebelumnya.
Mengalikan pembilang dengan penyebut
Jika Anda ingin memeriksa kesetaraan antara dua pecahan, Anda dapat menggunakan prosedur pertama ini. Pada dasarnya, Anda harus mengalikan pembilang pecahan pertama dengan penyebut pecahan kedua. Selanjutnya, Anda perlu mengalikan pembilang pecahan kedua dengan penyebut pecahan pertama. Jika kedua hasil memberikan hasil yang sama , maka pecahan tersebut akan setara. Lihatlah contoh berikut:
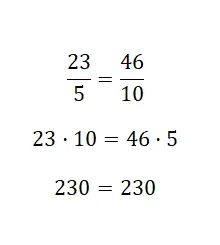
Dalam contoh terakhir ini, kami memverifikasi bahwa kedua pecahan itu ekuivalen. Contoh ini mudah dilihat, karena pecahan kedua adalah dua kali lipat pecahan pertama, artinya pecahan tersebut mempunyai hubungan ekuivalensi yang diperkuat . Perlu dicatat bahwa prosedur ini cukup nyaman digunakan, cukup memperbanyak tanda silang saja. Namun kami juga menyarankan Anda mempelajari cara menggunakan dua sistem lainnya, karena ini akan memberi Anda lebih banyak sumber daya matematika yang dapat Anda gunakan.
Sederhanakan pecahan
Untuk pecahan yang tidak dapat direduksi , kita dapat menggunakan metode lain yang terdiri dari mereduksi sebanyak mungkin pecahan yang terdiri dari bilangan terbesar. Jika, dalam melakukan reduksi ini, kita menemukan bahwa pecahan yang lebih kecil merupakan pecahan yang tidak dapat direduksi terhadap pecahan yang lain, maka kita dapat berasumsi bahwa pecahan tersebut ekuivalen.
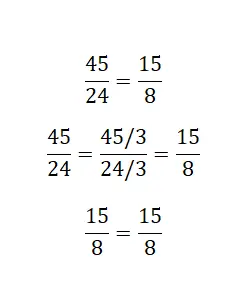
Menyelesaikan dan menyamakan perpecahan
Terakhir, Anda dapat menggunakan solusi hasil bagi yang dihasilkan oleh pecahan, karena bilangan campuran selalu merupakan pembagian. Pada dasarnya, Anda perlu menghitung nilai numerik ekuivalen kedua pecahan, dan jika angkanya sama, maka keduanya akan ekuivalen. Pada gambar berikut Anda dapat melihat contoh yang sangat jelas:
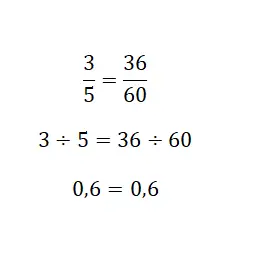
Latihan pecahan senilai
Sekarang setelah Anda membaca keseluruhan teorinya, Anda dapat mencoba menyelesaikan latihan berikut, yang akan memungkinkan Anda menyelesaikan pemahaman penjelasannya. Kami menyarankan Anda mencoba menyelesaikannya sendiri dan setelah Anda memilikinya, bandingkan hasil Anda dengan yang kami tawarkan kepada Anda. Oleh karena itu, kami mengizinkan Anda berlatih:
Latihan 1
Temukan pecahan senilai dengan menyederhanakan setiap pecahan yang kami tawarkan:
Untuk menyelesaikan latihan ini, cukup terapkan penyederhanaan pecahan, sehingga diperoleh pecahan tak tersederhanakan yang setara. Keempat contoh tersebut sangat mirip, sehingga tidak banyak kesulitan dalam menyelesaikannya.
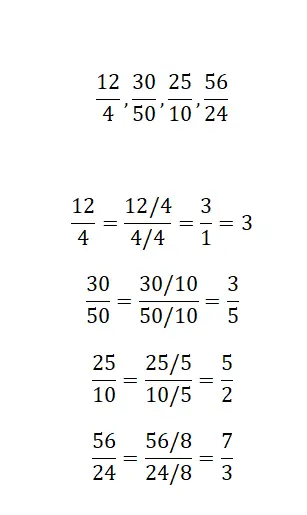
Latihan 2
Temukan pecahan senilai dengan amplifikasi untuk setiap pecahan yang kami usulkan:
Selanjutnya Anda harus memperbesar pecahan yang kami usulkan, dengan cara ini Anda akan mendapatkan pecahan senilai yang lebih besar. Tidak masalah bilangan apa yang digunakan untuk melakukan perkalian, misalnya kita akan melakukannya dengan 2 dan 3.
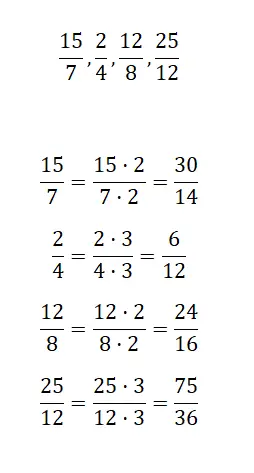
Latihan 3
Tentukan apakah pecahan berikut ekuivalen atau tidak:
Untuk mengetahui apakah dua pecahan setara, Anda perlu menggunakan salah satu dari tiga cara yang kami jelaskan di atas. Anda akan menemukan perbaikan diselesaikan dengan prosedur pertama, meskipun Anda bebas menggunakan sistem yang Anda inginkan.
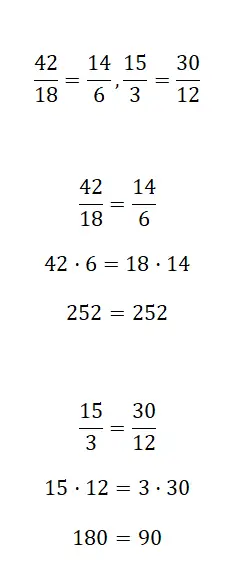
Latihan 4
Hitung pecahan senilai dari ekspresi berikut:
Dalam latihan terakhir ini Anda harus menulis ulang ekspresi yang kami usulkan ( bilangan bulat dan bilangan campuran) dalam bentuk pecahan, berusaha menjaga hubungan ekuivalen.