Pecahan tak tersederhanakan adalah pecahan yang tidak dapat disederhanakan lagi, sehingga tidak mempunyai pecahan senilai yang lebih kecil. Dengan kata lain, gcf pembilang dan penyebut suatu pecahan tak tersederhanakan sama dengan 1, karena tidak ada pembagi persekutuan lainnya. Misalnya, ungkapan “5/8” tidak dapat direduksi lagi, sehingga kita menyebutnya dalam bentuk yang paling sederhana atau tidak dapat direduksi.
Kalkulator pecahan tak tersederhanakan
Sebelum melanjutkan teorinya, kami ingin menunjukkan kepada Anda sebuah kalkulator, yang memungkinkan Anda mendapatkan pecahan tak tersederhanakan dari bilangan campuran apa pun. Yang harus Anda lakukan adalah memasukkan nilai pembilang dan penyebutnya lalu klik “Sederhanakan pecahan” , Anda kemudian akan mendapatkan bentuk tereduksi di kotak hasil. Kami merekomendasikan penggunaan alat ini untuk segera menyederhanakan pecahan apa pun atau bahkan untuk mengoreksi latihan pecahan Anda.
Apa yang dimaksud dengan pecahan tak tersederhanakan dan bagaimana cara menghitungnya?
Seperti yang sudah kami jelaskan di awal, pecahan tak tersederhanakan adalah pecahan yang tidak dapat disederhanakan lebih lanjut, sehingga merupakan pecahan langsung . Jika Anda ingin mencari pecahan jenis ini, Anda harus menggunakan penyederhanaan pecahan , dengan cara ini Anda akan menemukan pecahan senilai yang tidak dapat direduksi terhadap pecahan awal. Di tautan terakhir ini Anda dapat menemukan panduan rinci tentang menyederhanakan pecahan, meskipun dalam daftar berikut kami menjelaskan langkah-langkahnya secara ringkas:
- Menemukan Faktor Persekutuan: Untuk memulai, Anda perlu mencari faktor persekutuan terbesar dari pembilang dan penyebutnya. Dengan cara ini Anda mendapatkan angka yang memungkinkan Anda mengurangi kedua nilai sambil mempertahankan kesetaraan.
- Bagilah pecahan tereduksi dengan gcf: Setelah Anda mendapatkan gcf, Anda perlu membagi pembilang dan penyebutnya dengan pembagi persekutuan ini. Ini akan menghasilkan pembilang dan penyebut yang lebih sederhana (atau lebih kecil).
Anda juga dapat menggunakan cara lain untuk mencari pecahan tak tereduksi, seperti yang dijelaskan dalam artikel kami tentang menyederhanakan pecahan. Meskipun dengan metodologi yang telah kami jelaskan kepada Anda, Anda dapat mengurangi pecahan apa pun yang Anda inginkan dengan sangat mudah dan cepat.
Contoh pecahan tereduksi dan pecahan tak tereduksi
Pada gambar berikut Anda dapat menemukan empat contoh pecahan tereduksi dan empat contoh pecahan tak tereduksi lainnya. Sebaiknya Anda mencoba menyederhanakan masing-masing pecahan, dengan cara ini Anda akan memahami dengan jelas perbedaan kedua jenis pecahan tersebut.
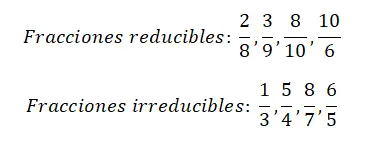
Contoh penghitungan pecahan tak tersederhanakan
Di sini kami menunjukkan kepada Anda langkah demi langkah bagaimana Anda dapat menyederhanakan pecahan menggunakan dua metode. Yang pertama menunjukkan prosedur lengkap yang kami jelaskan di bagian sebelumnya. Dan yang kedua menunjukkan sistem yang agak berbeda, yang melibatkan pembagian pembilang dan penyebut dengan nilai yang sama, dimulai dari pembagi terkecil (tidak termasuk 1) dan seterusnya. Namun jika menurut Anda sistem kedua terlalu rumit, Anda bisa mengabaikannya.
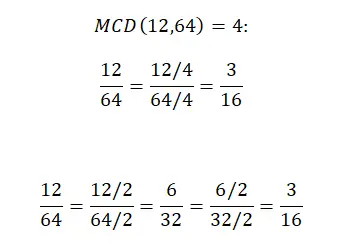
Pecahan tak tersederhanakan dari suatu bilangan desimal
Pecahan tak tersederhanakan yang diperoleh dari suatu bilangan desimal disebut pecahan pembangkit . Penting untuk dicatat bahwa ini dihitung dengan cara yang berbeda tergantung pada jenis desimal yang kita hadapi (eksak, periodik murni, atau periodik campuran). Contoh berikut dengan jelas menunjukkan konsep matematika ini: 5/7 = 0,7142857... Seperti yang Anda lihat, lima pertujuh adalah pecahan tak tersederhanakan yang setara dengan angka desimal 0,7142857...
Bagaimana cara mengetahui suatu pecahan tidak dapat direduksi?
Untuk mengetahui apakah suatu pecahan dapat direduksi atau tidak dapat direduksi, Anda dapat mengikuti dua cara. Yang pertama adalah menghitung pembagi persekutuan terbesar dari pembilang dan penyebutnya, jika nilainya berbeda dari satu berarti itu adalah pecahan yang dapat direduksi. Dan jika Anda mendapatkan satu sebagai hasilnya, Anda tahu bahwa pecahan tersebut tidak dapat direduksi. Kedua, Anda dapat menggunakan kalkulator pecahan tak tereduksi yang kami tunjukkan di awal untuk melakukan pemeriksaan jenis ini.
Latihan soal pecahan tak tersederhanakan
Sekarang setelah Anda membaca teorinya, kami menyarankan Anda mencoba menyelesaikan soal-soal ini , yang memungkinkan Anda berlatih menghitung pecahan tak tersederhanakan. Selain itu, jika Anda ingin meningkatkan pemahaman Anda tentang bilangan campuran, kami sarankan untuk mencoba menyelesaikan latihan pecahan ini. Melalui ini Anda akan lebih memahami konsep pecahan itu sendiri.
Latihan 1
Hitunglah pecahan tak tersederhanakan dari pecahan-pecahan tereduksi berikut ini. Ingat, Anda bisa menggunakan metode apa pun untuk menyederhanakan pecahan. Dan setelah Anda menyelesaikan latihan, Anda dapat membandingkan hasil Anda dengan hasil yang kami tunjukkan pada gambar di bawah.
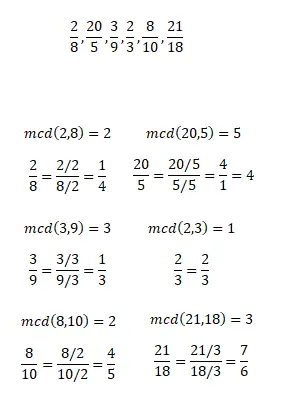
Latihan 2
Tentukan pecahan yang senilai dengan pecahan tak tersederhanakan 2/3 dan 4/5. Untuk menyelesaikan tugas ini, kami sarankan untuk melihat angka-angka pada pembilang dan penyebutnya, serta memikirkan hubungan pembagiannya. Mungkin Anda dapat menggunakan faktor persekutuan terbesar atau kelipatan persekutuan terkecil untuk menemukan apa yang Anda cari...
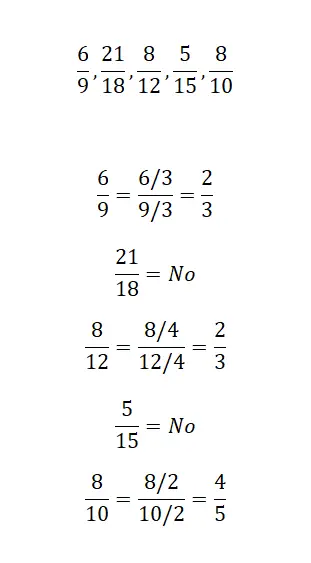
Latihan 3
Pada latihan terakhir ini, Anda hanya perlu menunjukkan apakah ketiga pecahan berikut mempunyai pecahan tak tersederhanakan yang sama. Oleh karena itu, ketiga pecahan perlu direduksi sebanyak mungkin dan dianalisis hasilnya. Setelah Anda menyelesaikannya, Anda dapat membandingkan solusi Anda dengan solusi kami.
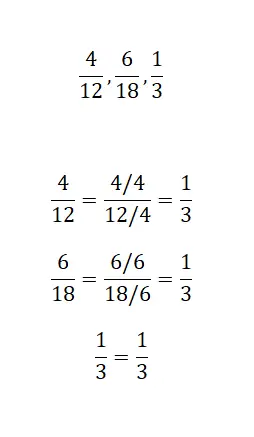
Informasi lebih lanjut tentang pecahan
Kami harap artikel ini membantu Anda memahami pecahan tak tersederhanakan. Meskipun jika Anda memiliki pertanyaan, silakan baca penjelasan kami tentang pecahan . Di sana Anda akan menemukan semua informasi tentang pecahan: definisi, kategori, operasi dan latihan, semuanya dijelaskan menggunakan teori dan contoh. Kami meyakinkan Anda bahwa jika Anda membaca artikel ini Anda akan menghilangkan banyak keraguan mendasar terkait topik ini.