Halaman ini menjelaskan apa saja titik potong (atau perpotongan) suatu fungsi dengan sumbu kartesius dan cara menghitungnya. Selain itu, Anda akan menemukan beberapa contoh untuk memahami sepenuhnya bagaimana hal tersebut ditemukan dan Anda bahkan dapat berlatih dengan latihan yang diselesaikan langkah demi langkah.
Berapakah titik potong (atau perpotongan) suatu fungsi dengan sumbunya?
Sebelum melihat cara menghitungnya, mari kita ingat apa saja titik potong suatu fungsi dengan sumbunya.
Titik potong atau titik potong sumbu adalah titik-titik yang representasi suatu fungsi memotong sumbu-sumbu koordinat, yaitu titik-titik pada grafik yang berikatan pada sumbu X dan sumbu l. sumbu Y.
Misalnya parabola pada grafik berikut memotong sumbu Y di titik (0,3) dan memotong sumbu X di titik (-1,0) dan (3,0).
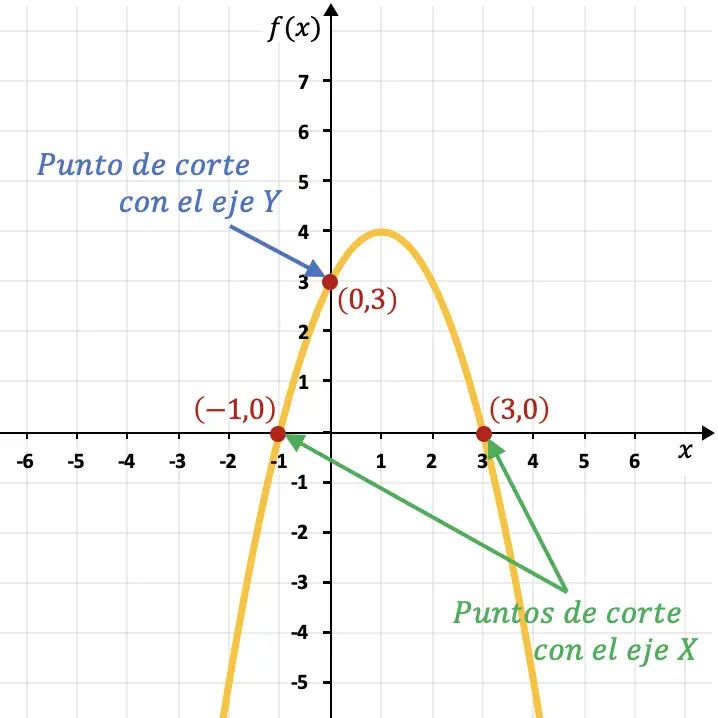
Titik potong suatu fungsi dengan sumbu X
Koordinat kedua titik potong suatu fungsi dengan sumbu X selalu 0, maka:
Titik potong dari setiap fungsi sumbu x OX berbentuk
![]()
, dan dapat dihitung dengan menyelesaikan persamaan berikut:
![]()
Terkadang saat menyelesaikan persamaan ini kita bisa mendapatkan dua (atau lebih) solusi, artinya fungsi tersebut memotong sumbu X dua (atau lebih) kali. Sebaliknya, jika persamaan tersebut tidak mempunyai penyelesaian, berarti fungsi tersebut tidak memotong sumbu X.
Titik potong suatu fungsi dengan sumbu Y
Koordinat pertama titik potong suatu fungsi dengan sumbu Y selalu sama dengan 0, maka:
Titik potong suatu fungsi dengan sumbu y OY berbentuk
![]()
, dan dapat dicari dengan menghitung bayangan fungsi di x=0:
![]()
Berbeda dengan breakpoint pada sumbu X, hanya terdapat satu breakpoint pada sumbu Y.
Contoh penghitungan titik potong suatu fungsi dengan sumbu
Agar Anda tidak ragu lagi, di bawah ini kita akan melihat contoh cara mencari titik potong suatu fungsi dengan sumbu kartesius:
- Temukan secara numerik titik potong dari fungsi berikut:
![]()
Pertama-tama kita akan menghitung titik potong fungsi tersebut dengan sumbu x. Titik potong dengan sumbu X akan selalu memiliki komponen kedua sama dengan 0, artinya bertipe
![]()
. Karena f(x) selalu sama dengan 0 pada sumbu OX. Jadi untuk mencari komponen titik lainnya kita perlu menyelesaikan persamaannya
![]()
![]()
![]()
![]()
![]()
Maka titik potongnya dengan sumbu X adalah:
![]()
Sekarang kita akan mencari titik potong dengan sumbu y. Titik perpotongan dengan sumbu Y akan selalu mempunyai komponen pertama sama dengan 0, artinya titik tersebut akan bertipe
![]()
. Karena variabel bebas x selalu hilang pada sumbu Y. Jadi untuk mencari koordinat titik lainnya kita perlu menghitungnya
![]()
![]()
Maka titik potongnya dengan sumbu Y adalah:
![]()
Di bawah ini Anda memiliki contoh fungsi yang direpresentasikan secara grafis, Anda dapat melihat bahwa ambang batas yang ditemukan bertepatan dengan ambang batas yang ada pada grafik:
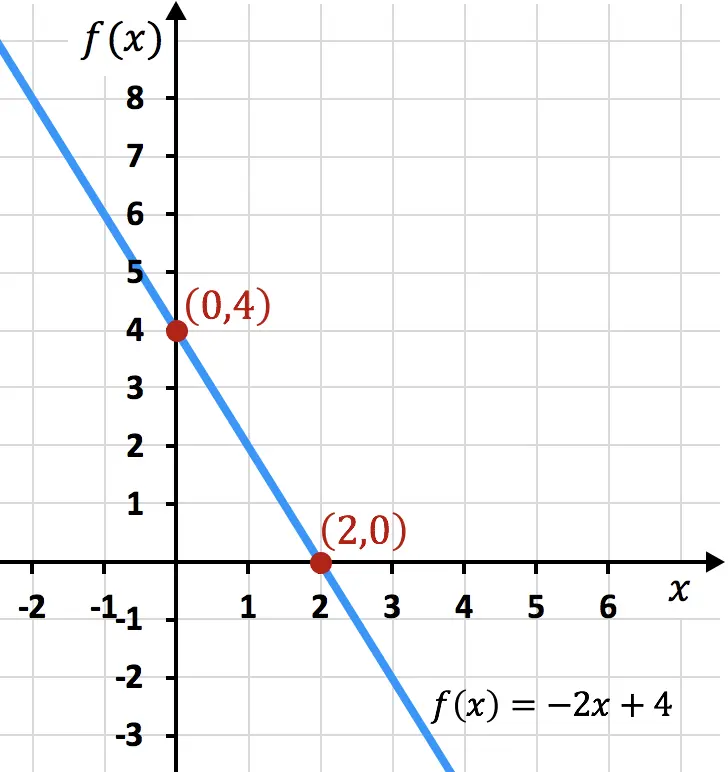
Latihan yang diselesaikan untuk titik potong suatu fungsi dengan sumbu
Latihan 1
Tentukan titik potong dengan sumbu koordinat fungsi berikut:
![]()
Titik potong dengan sumbu X
Untuk mencari titik potong fungsi tersebut dengan sumbu X perlu dicari penyelesaiannya
![]()
![]()
![]()
![]()
![]()
Oleh karena itu, titik potong fungsi tersebut dengan sumbu X adalah:
![]()
Titik potong dengan sumbu Y
Untuk mencari titik potong dengan sumbu Y harus dilakukan perhitungan
![]()
![]()
Oleh karena itu, titik potong fungsi tersebut dengan sumbu Y adalah:
![]()
Latihan 2
Tentukan titik potong sumbu kartesius dari fungsi affine berikut:
![]()
Titik potong dengan sumbu X
Untuk mencari titik limit suatu fungsi dengan sumbu OX, kita perlu mengatur fungsinya sama dengan nol dan menyelesaikan persamaan yang dihasilkan:
![]()
![]()
![]()
![]()
Jadi titik potong fungsi tersebut dengan sumbu absis adalah:
![]()
Titik potong dengan sumbu Y
Untuk mencari titik potong dengan sumbu OY, kita perlu melakukan perhitungan
![]()
![]()
Oleh karena itu, titik potong fungsi tersebut dengan sumbu komputer adalah:
![]()
Latihan 3
Hitung titik potong dengan sumbu fungsi kuadrat berikut:
![]()
Titik potong dengan sumbu X
Untuk mencari titik potong fungsi tersebut dengan sumbu X perlu dicari penyelesaiannya
![]()
![]()
![]()
Dalam hal ini, kita perlu menyelesaikan persamaan kuadrat, jadi kita menerapkan rumus:
![]()
![Rendered by QuickLaTeX.com \displaystyle x=\cfrac{ -(-3) \pm \sqrt{(-3)^2-4\cdot 1 \cdot 2}}{2\cdot 1} = \cfrac{3 \pm 1}{2} = \begin{cases} 2 \\[2ex] 1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-47048fdd48ce98ba99629edf5a379f76_l3.png)
Kami memperoleh dua solusi persamaan kuadrat, sehingga fungsinya memotong sumbu X di dua titik:
![]()
Titik potong dengan sumbu Y
Sedangkan untuk menentukan titik potong dengan sumbu Y perlu dilakukan perhitungan
![]()
![]()
Oleh karena itu, satu-satunya titik potong fungsi tersebut dengan sumbu Y adalah:
![]()
Latihan 4
Temukan titik potong dengan sumbu bidang kartesius dari fungsi rasional berikut:
![]()
Titik potong dengan sumbu X
Untuk mencari titik potong fungsi tersebut dengan sumbu X perlu dicari penyelesaiannya
![]()
![]()
![]()
![]()
![]()
![]()
5 tidak setara dengan 0, sehingga persamaan tersebut tidak memiliki solusi dan oleh karena itu, tidak ada titik potong antara fungsi tersebut dan sumbu X.
Titik potong dengan sumbu Y
Untuk mencari titik potong dengan sumbu Y harus dilakukan perhitungan
![]()
![]()
Bilangan apa pun yang dibagi nol merupakan suatu ketidakpastian yang menghasilkan bilangan tak terhingga. Oleh karena itu, fungsinya tidak melampaui sumbu Y di titik mana pun.
Singkatnya, fungsi latihan tidak memiliki titik potong dengan sumbu , artinya grafiknya tidak melalui sumbu X atau sumbu Y di titik mana pun.
Latihan 5
Hitung titik potong dengan sumbu fungsi derajat ketiga berikut:
![]()
Titik potong dengan sumbu X
Untuk mencari titik potong fungsi tersebut dengan sumbu X perlu dicari penyelesaiannya
![]()
![]()
![]()
Kedua suku persamaan tersebut mempunyai x , yang dengannya kita dapat mengekstrak faktor persekutuannya:
![]()
Agar persamaan sebelumnya terpenuhi, salah satu faktornya harus 0. Oleh karena itu, kita tetapkan setiap faktor sama dengan nol untuk mendapatkan semua solusi yang mungkin:
![Rendered by QuickLaTeX.com \displaystyle x(x^2-9)=0 \ \longrightarrow \begin{cases} \bm{x = 0} \\[2ex] x^2-9 = 0\ \longrightarrow \ x^2=9 \ \longrightarrow \ \bm{x=\pm 3} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-37febaed85a502533604305b9009611d_l3.png)
Oleh karena itu kita memperoleh tiga solusi persamaan derajat ketiga, sehingga fungsinya memotong sumbu X menjadi 3 titik:
![]()
Titik potong dengan sumbu Y
Untuk menghitung titik potong dengan sumbu Y, Anda perlu melakukan perhitungan
![]()
![]()
Oleh karena itu, satu-satunya titik potong fungsi tersebut dengan sumbu Y adalah titik asal koordinat (0,0):
![]()
Perhatikan bahwa kita telah menemukan titik ini dalam perhitungan titik potong dengan sumbu X, karena fungsinya memotong pada titik ini dengan kedua sumbu secara bersamaan.