Pecahan atau bilangan campuran merupakan konsep matematika yang sangat penting dalam bidang kalkulus. Oleh karena itu, penting untuk mengetahui cara kerjanya dan cara menyelesaikan latihan pecahan . Inilah tujuan artikel ini, apakah Anda mempelajari cara menyelesaikan operasi pecahan dan jenis latihan atau soal lainnya yang mencakup bilangan dengan gaya ini. Oleh karena itu, mari kita mulai dengan latihan pertama.
Latihan operasi pecahan
Untuk memulai, kami menyediakan beberapa operasi dasar yang mencakup pecahan, Anda hanya perlu menyelesaikannya dan menyatakan hasil yang disederhanakan. Jadi, setelah Anda selesai menyelesaikan perhitungan , kami menyarankan Anda membandingkan hasilnya dan melihat koreksi yang kami tawarkan kepada Anda. Meskipun Anda juga dapat memeriksa hasilnya dengan kalkulator pecahan online kami.
Penjumlahan dan pengurangan pecahan yang mempunyai penyebut yang sama
Di bawah ini Anda telah menyelesaikan dua penjumlahan dan dua pengurangan pecahan, coba selesaikan sendiri dan bandingkan hasilnya. Dengan cara ini, Anda akan meninjau mekanisme penyelesaian untuk jenis operasi ini:
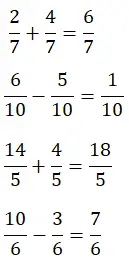
Penjumlahan dan pengurangan pecahan yang penyebutnya berbeda
Sekarang kita naikkan levelnya sedikit, karena untuk menyelesaikan penjumlahan dan pengurangan pecahan yang penyebutnya berbeda, kita perlu mencari lcm penyebutnya terlebih dahulu. Oleh karena itu, perhitungannya menjadi sedikit lebih rumit.
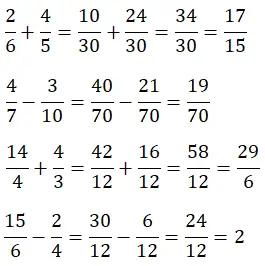
Mengalikan dan membagi pecahan
Pada bagian ini Anda harus menyelesaikan perkalian dan pembagian pecahan, operasi ini sangat mudah dilakukan, namun Anda tetap perlu mempraktikkannya. Seperti pada dua bagian sebelumnya, Anda memiliki dua untuk setiap tipe.
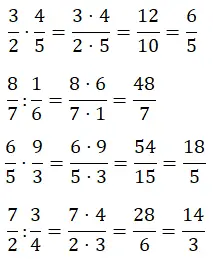
pecahan gabungan
Terakhir, Anda harus menyelesaikan pecahan gabungan , yang merupakan operasi gabungan dengan pecahan. Elemen yang paling rumit adalah perhitungannya, karena Anda harus mengumpulkan seluruh pengetahuan Anda tentang operasi bilangan campuran agar dapat menyelesaikan perhitungan jenis ini dengan benar.

Latihan konversi antara desimal dan pecahan
Anda sekarang harus mencoba mengubah bilangan desimal berikut menjadi pecahan pembangkit dan sebaliknya. Meskipun untuk melakukannya dengan benar, Anda perlu mempertimbangkan jenis desimal (eksak, periodik murni, atau periodik campuran) karena metode konversinya berbeda-beda. Jika Anda tidak ingat cara-cara ini, kami sarankan membaca artikel kami tentang pecahan , karena di sana kami menjelaskan semua tata cara mengubah desimal ke pecahan dan sebaliknya. Di bawah ini Anda dapat menemukan beberapa konversi terpecahkan, kami menyarankan Anda mencoba melakukannya sendiri:

Latihan pecahan senilai
Setelah berlatih aritmatika dasar dan konversi, sekarang saatnya memulai dengan pecahan senilai . Pada bagian ini kami akan menunjukkan kepada Anda beberapa pecahan dan Anda perlu mencari pasangan pecahan yang senilai. Dengan cara ini Anda akan berlatih konsep kesetaraan dan juga mengulas penyederhanaan pecahan .

Latihan perbandingan pecahan
Selanjutnya, kami akan menunjukkan beberapa pecahan dan Anda harus membandingkannya dengan simbol “<“, “=” dan “>”. Untuk menyelesaikan latihan ini, Anda perlu mencari penyebut yang sama dan mengubah kedua pecahan menjadi penyebut tersebut. Dengan cara ini Anda akan dapat melihat mana di antara dua pembilang yang lebih besar, dan Anda harus bertindak berdasarkan hal tersebut:

Latihan pecahan pada garis bilangan
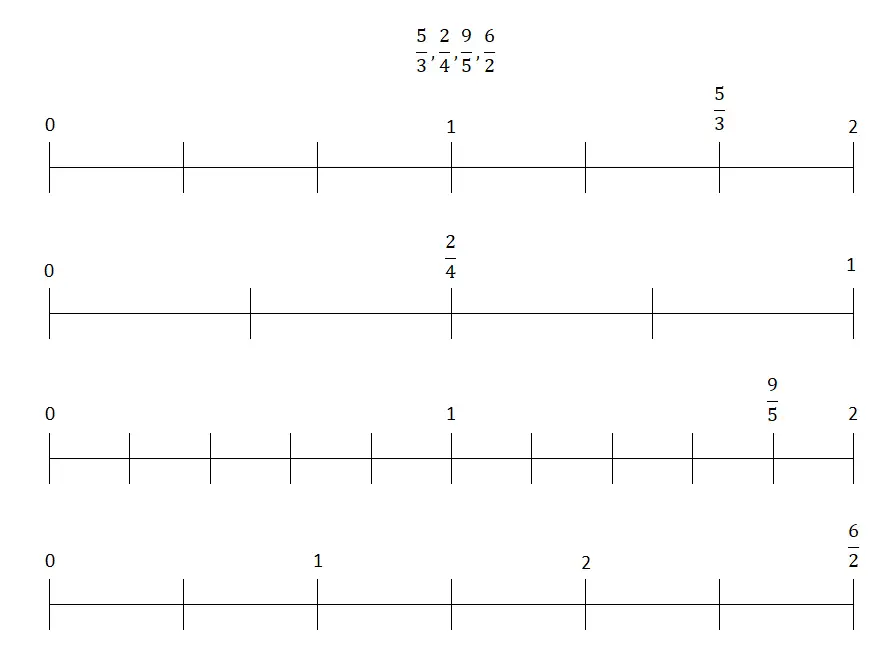
Dalam latihan ini Anda harus mengurutkan pecahan-pecahan berbeda yang akan kami berikan kepada Anda pada garis bilangan , sehingga prosedur penyelesaiannya bisa sangat bervariasi. Misalnya, Anda dapat membagi jarak antara dua bilangan bulat dengan bagian sebanyak yang ditunjukkan oleh nilai penyebutnya, lalu letakkan pecahan tersebut di ruas yang ditunjukkan oleh pembilangnya .
Selain itu, Anda dapat membagi pembilang dengan penyebutnya dan mendapatkan angka desimal, yang nantinya akan Anda tempatkan pada garis. Meskipun prosedur kedua ini jauh lebih mendasar , itulah sebabnya kami memilih metode pertama yang telah kami jelaskan. Meskipun demikian, pecahan yang perlu Anda tempatkan di sebelah kanan adalah sebagai berikut:
masalah pecahan
Akhirnya, kita sampai pada bagian terakhir artikel ini, di mana kita akan membahas beberapa soal pecahan. Meskipun pertama-tama, kami ingin menjelaskan prosedur yang benar yang harus Anda gunakan saat menyelesaikan masalah matematika :
- Pahami masalahnya: Langkah pertama adalah melakukan pembacaan yang baik, sehingga Anda memahami keseluruhan masalahnya. Dengan cara ini Anda akan membiasakan diri dengan semua informasi yang dijelaskan dalam deklarasi. Jika Anda melakukan bagian ini dengan benar, maka Anda telah mencapai banyak hal, karena Anda akan mengetahui cara mengarahkan solusi dan semua perhitungannya.
- Pernyataan Masalah: Setelah Anda mengetahui apa masalahnya, Anda perlu mempresentasikannya. Anda dapat melakukan ini menggunakan bagan, gambar, atau representasi grafis kecil dari data. Pada langkah ini, Anda akan mulai memikirkan cara untuk menghubungkan data dan memecahkan masalah.
- Selesaikan masalahnya sendiri: Nantinya Anda dapat melanjutkan menyelesaikan masalah secara numerik, pada tahap ini Anda perlu menguji teori-teori yang Anda kemukakan pada bagian sebelumnya. Di sinilah Anda benar-benar menjalankan rencana tindakan dan mendapatkan hasilnya, jadi Anda harus sangat fokus.
- Menafsirkan solusinya: Terakhir, ketika Anda sudah memiliki solusinya, Anda perlu menafsirkan hasil-hasil tersebut dan memahaminya dalam konteks masalahnya. Langkah terakhir ini sangat penting dan banyak orang yang mengabaikannya, karena menganggap hasil numerik saja sudah cukup, namun kenyataannya Anda harus merangkum solusinya dalam satu kalimat.
masalah 1
Jika kita ingin mengisi kolam dengan sekali keran membutuhkan waktu 6 jam, namun jika dengan keran yang lain membutuhkan waktu 8 jam. Berapa banyak kolam yang akan terisi dalam waktu 2 jam jika kita menggunakan kedua keran secara bersamaan? Nyatakan hasilnya sebagai pecahan.
Untuk menyelesaikan soal ini, kita perlu menggunakan pecahan. Pada dasarnya yang akan kita lakukan adalah menghitung secara terpisah berapa banyak setiap faucet akan terisi selama dua jam tersebut. Jadi, keran pertama akan mengisi 1/6 tangki dalam satu jam dan jika dikalikan dengan dua jam, maka akan terisi 2/6. Sedangkan keran kedua akan mengisi 1/8 dalam satu jam dan kita juga harus mengalikannya dengan 2, sehingga kita mendapatkan 2/8.
Terakhir, kita akan menjumlahkan kedua pecahan tersebut, untuk mendapatkan jumlah total pool yang telah terisi. Jadi yang tersisa adalah 2/6 + 2/8 = 7/12 dari kumpulan tersebut.
masalah 2
Kami punya 64 permen, tapi 1/4nya kami berikan kepada teman kami Marcos. Lalu kami makan 3 permen dan memberikan 2/5 sisanya kepada teman kami María. Berapa banyak permen yang tersisa? Nyatakan sebagai bilangan bulat.
Pertama kita perlu mengurangi seperempat dari jumlah total 64, lalu kita kurangi 3 dari hasil yang didapat dan terakhir kita kurangi dua perlima dari jumlah permen tersebut. Dengan itu, kita dapat menghitungnya dengan gabungan pecahan:
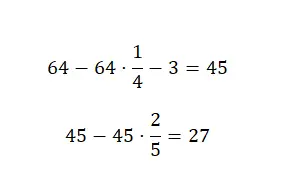
Oleh karena itu, pada akhirnya kita hanya mempunyai 27 permen.
masalah 3
Kami mempunyai sebidang tanah seluas 10.000 m² yang dibagi menjadi tiga bagian yang tidak sama. Bagian pertama mewakili 3/6 dari total luas dan bagian kedua sama dengan setengah dari bagian sebelumnya. Pecahan manakah yang menggambarkan luas bagian ketiga? Berapa meter persegi yang dimiliki setiap sektor?
Hal pertama yang akan kita lakukan adalah menghitung pecahan dari plot ketiga, kita akan melakukannya dengan cara pengurangan pecahan yang sangat sederhana. Selanjutnya kita akan menghitung luas setiap bagian dengan menghitung pecahan suatu bilangan, dalam kasus kita nilai numeriknya adalah 10.000. Di bawah ini Anda dapat melihat seluruh prosedur: