Di halaman ini Anda akan mempelajari apa itu fungsi eksponensial dan juga cara merepresentasikan fungsi eksponensial pada grafik. Selain itu, Anda akan melihat semua karakteristiknya dan beberapa contoh untuk memahaminya sepenuhnya. Terakhir, Anda akan dapat berlatih dengan latihan dan soal yang diselesaikan selangkah demi selangkah tentang fungsi eksponensial.
Apa itu fungsi eksponensial?
Pengertian fungsi eksponensial adalah sebagai berikut:
Dalam matematika, fungsi eksponensial adalah fungsi yang mempunyai variabel bebas x dalam pangkat. Dengan kata lain, mereka adalah sebagai berikut:
![]()
Emas
![]()
adalah bilangan real positif dan berbeda dengan 1.
Contoh Fungsi Eksponensial
Fungsi berikut adalah contoh fungsi eksponensial:
![]()
![]()
![]()
![]()
Karakteristik fungsi eksponensial
Fungsi eksponensial mempunyai sifat sebagai berikut:
- Domain fungsi eksponensial terdiri dari bilangan real, atau dengan kata lain fungsi eksponensial ada untuk nilai x apa pun.
![]()
- Namun fungsi tersebut hanya bernilai positif, sehingga rentang fungsi eksponensial terdiri dari bilangan real positif.
![]()
- Setiap fungsi eksponensial merupakan fungsi kontinu dan fungsi injektif.
- Jika fungsi tersebut tidak diterjemahkan, setiap fungsi eksponensial melewati titik (0,1). Karena fungsi yang dievaluasi ke nol selalu menghasilkan satu.
![]()
- Demikian pula, nilai fungsi eksponensial pada x=1 sama dengan basis.
![]()
- Jika basis kekuatan
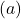
lebih besar dari 1, fungsi eksponensialnya meningkat. Sebaliknya jika koefisiennya

berada pada interval antara 0 dan 1, fungsi eksponensialnya menurun.
- Secara umum sumbu x merupakan asimtot horizontal dari suatu fungsi eksponensial.
- Kebalikan dari fungsi eksponensial adalah fungsi logaritma. Oleh karena itu, grafik fungsi eksponensial dan fungsi logaritma adalah simetris terhadap garis y=x jika keduanya mempunyai basis yang sama.
Cara Membuat Grafik Fungsi Eksponensial
Fungsi eksponensial sangat sederhana untuk direpresentasikan. Jadi mari kita lihat cara membuat grafik fungsi eksponensial pada grafik menggunakan sebuah contoh.
- Gambarkan fungsi eksponensial berikut pada grafik:
![]()
Dalam fungsi eksponensial, domain tidak perlu dihitung karena semuanya akan selalu berupa bilangan real:
![]()
Oleh karena itu, cukup dengan menyusun tabel nilai. Karena jenis fungsi ini banyak berubah dari satu titik ke titik lainnya, kita akan menghitung 5 poin. Namun semakin banyak poin yang kita hitung, representasi fungsinya akan semakin tepat.

Kami merekomendasikan penggunaan kalkulator untuk mencari poin dalam tabel nilai, karena rumit untuk dihitung dengan tangan.
Sekarang kita mewakili titik-titik pada grafik :

Dan terakhir, kami menggabungkan titik-titik tersebut dan memperluas fungsinya:
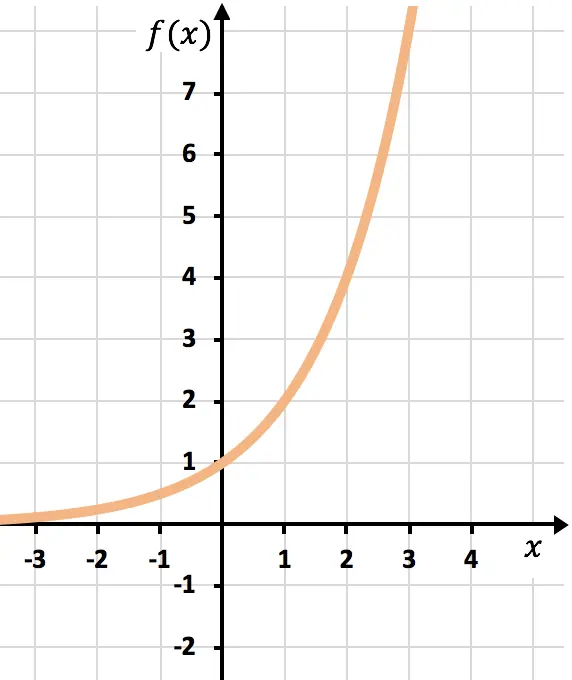
Perhatikan bahwa fungsi di sebelah kanan terus bertambah hingga tak terhingga.
Sebaliknya, fungsi di sebelah kiri berkurang tetapi tidak pernah mencapai 0. Meskipun sangat dekat dengannya, namun tidak pernah menyentuhnya. Artinya garis y=0 (sumbu x) merupakan asimtot mendatar.
Latihan soal fungsi eksponensial
Latihan 1
Gambarkan fungsi eksponensial berikut:
![]()
Ini adalah fungsi eksponensial, jadi untuk merepresentasikannya Anda harus membuat tabel nilai yang memberikan nilai pada variabel x:
![]()
![]()
![]()
![]()
![]()

Setelah kita memiliki tabel nilainya, kita memplot titik-titik yang diperoleh pada grafik dan memplot fungsinya:

Perhatikan bahwa fungsi di sebelah kanan terus bertambah hingga tak terhingga. Sebaliknya, di sebelah kiri, fungsinya berkurang tetapi tidak pernah melebihi 1. Memang benar, fungsi tersebut mempunyai asimtot horizontal di sebelah kanan y=1.
Dalam hal ini, asimtot horizontal berada di y=1 dan bukan pada sumbu OX karena translasi vertikal satu satuan ke atas telah dilakukan menuju fungsi tersebut.
Latihan 2
Gambarkan fungsi eksponensial berikut pada grafik:
![]()
Ini adalah fungsi eksponensial, jadi untuk merepresentasikannya secara grafis Anda harus membuat tabel nilai yang memberikan nilai pada variabel x:
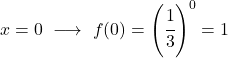
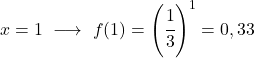
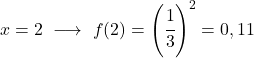
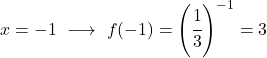
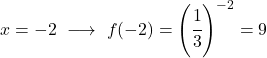
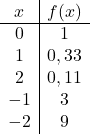
Setelah kita memiliki tabel nilainya, kita memplot titik-titik yang dihitung pada grafik dan menggambar fungsinya:

Perhatikan bahwa fungsi di sebelah kiri terus bertambah hingga tak terbatas. Di sisi lain, di sebelah kanan, fungsinya berkurang tetapi tidak pernah melebihi 0. Memang benar, fungsi tersebut memiliki asimtot horizontal di y=0 (sumbu X).
Latihan 3
Gambarkan fungsi eksponensial berikut pada grafik:
![]()
Ini adalah fungsi eksponensial, jadi untuk menggambarnya Anda harus membuat tabel nilai yang mengevaluasi fungsi tersebut di beberapa titik:
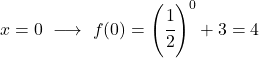
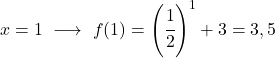
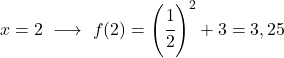
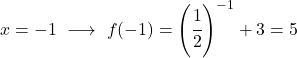
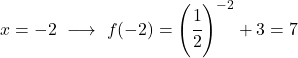

Terakhir, kami merepresentasikan titik-titik yang diperoleh pada grafik dan memplot fungsinya:

Perhatikan bahwa fungsi di sebelah kiri bertambah tanpa batas hingga tak terbatas. Sebaliknya, di sebelah kanan, fungsinya berkurang tetapi tidak pernah melebihi 3. Memang benar, fungsi tersebut mempunyai asimtot horizontal di y=3.
Dalam hal ini, asimtot horizontal berada di y=3 dan bukan di sumbu X karena fungsinya telah dipindahkan secara vertikal tiga satuan ke atas.
Latihan 4
Selesaikan soal berikut mengenai fungsi eksponensial.
- Tentukan nilai dari

sehingga fungsi eksponensial selanjutnya melalui titik (2.8).
![]()
Fungsi tersebut harus melalui titik (2,8), sehingga kita dapat mensubstitusikan nilai x dan f(x) titik tersebut ke dalam fungsi tersebut untuk mencari nilai konstanta k:
![]()
Dan sekarang kita selesaikan persamaan yang dihasilkan:
![]()
![]()
![]()
![]()
Latihan 5
Selesaikan soal berikut mengenai fungsi eksponensial.
Populasi rayap berkembang biak menurut fungsi berikut:
![]()
Emas
![]()
adalah jumlah rayap dan
![]()
waktu telah berlalu dalam beberapa bulan.
Berapa jumlah rayap setelah 1 tahun?
Untuk menghitung jumlah rayap dalam setahun, cukup masukkan waktu yang telah berlalu (1 tahun) ke dalam fungsi tersebut. Namun karena fungsi t adalah bulan yang telah berlalu dan bukan tahun, maka kita harus memasukkan t =12 karena dalam satu tahun terdapat 12 bulan:
![]()
![]()
![]()
Kami menyelesaikannya dengan kalkulator:
![]()
Jadi setelah satu tahun akan ada 1.594.323 rayap.