Géométrie analytique dans l’espace (formules)

Sur cette page vous trouverez l’explication de tout sur la géométrie analytique dans l’espace (et les formules) : les équations de la droite et du plan, les positions relatives entre plans et droites, comment sont calculés les distances et les angles dans l’espace,…

Qu’est-ce que la géométrie dans l’espace ?

La géométrie de l’espace est la branche de la géométrie chargée d’étudier les figures géométriques à trois dimensions (3D), c’est-à-dire qui occupent une place dans l’espace. Comme par exemple le cône, le cube, la pyramide, la sphère, le cylindre, les prismes, les polyèdres, etc.

Cependant, sur cette page, nous nous concentrerons sur la géométrie analytique dans l’espace , la partie de la géométrie de l’espace qui se concentre sur l’analyse des points, des lignes, des plans, les distances entre deux figures géométriques, l’angle qu’elles forment, les points d’intersection entre différentes figures géométriques. éléments, etc

Équations de la droite dans l’espace

Rappelons que la définition mathématique d’une ligne est un ensemble de points consécutifs représentés dans la même direction sans courbes ni angles.

Ainsi, pour exprimer mathématiquement n’importe quelle ligne dans un espace tridimensionnel (dans R3) on utilise les équations de la ligne, et pour les trouver il suffit d’un point qui appartient à la ligne et du vecteur directeur de ladite ligne.

Avec seulement ces deux éléments géométriques, vous pouvez trouver absolument toutes les différentes équations de la droite, qui sont les suivantes :

Les équations de la droite sont l’ équation vectorielle , les équations paramétriques , l’ équation continue et l’ équation implicite (ou générale) .

Ci-dessous vous avez une explication des différents types d’équations de la droite.

Équation vectorielle de la ligne dans l’espace

Ouais

est le vecteur directeur de la droite et un point qui appartient à la droite :

La formule de l’équation vectorielle de la droite est :

Equations paramétriques de la droite dans l’espace

Nous pouvons obtenir la formule de l’équation paramétrique d’une droite à partir de son équation vectorielle en assimilant composante à composante :

Équation continue de la droite dans l’espace

La formule de l’ équation continue de la droite est :

Ce type d’équation de la droite peut également être obtenu à partir d’équations paramétriques, vous pouvez voir la démonstration sur notre page de l’ équation continue , de plus, vous pourrez également voir des exemples et pratiquer avec des exercices résolus des équations de la droite .

Équations générales (ou implicites) de la droite dans l’espace

Enfin, en multipliant les fractions de l’équation continue de la droite deux par deux, on obtient les équations générales (ou implicites) de la droite :

Ce type d’équation de la droite est aussi appelé équation cartésienne.

Nous venons de voir les 4 équations les plus pertinentes de la droite (vecteur, paramétrique, continue et générale), cependant, il existe une autre équation un peu particulière et, par conséquent, il faut une page entière pour l’expliquer. C’est l’ équation canonique , dans ce lien vous pouvez voir toute son explication, pourquoi elle est si spéciale et ce qui la rend différente de toutes les autres.

Équations du plan dans l’espace

En géométrie analytique, l’ équation d’un plan est une équation qui permet d’exprimer analytiquement n’importe quel plan. Ainsi, pour trouver l’équation d’un plan, vous n’avez besoin que d’un point et de deux vecteurs linéairement indépendants appartenant audit plan.

Ainsi, tous les types d’équations du plan sont : l’ équation vectorielle , les équations paramétriques , l’ équation implicite (ou générale) et l’ équation canonique (ou segmentaire) du plan.

Ensuite nous allons voir l’explication et la formule de toutes les équations du plan.

Équation vectorielle du plan

Étant donné un point et deux vecteurs directeurs d’un plan :

La formule de l’équation vectorielle d’un plan est :

Ou équivalent:

Où

et Ce sont deux scalaires, c’est-à-dire deux nombres réels.

Équations paramétriques du plan

D’autre part, la formule de l’ équation paramétrique du plan est :

Équation implicite ou générale du plan

L’équation implicite d’un plan, également appelée équation générale, est obtenue en résolvant le déterminant suivant et en fixant le résultat à 0 :

Ainsi l’ équation implicite ou générale du plan résultant sera de la forme suivante :

Ce type d’équation plane est également appelé équation plane cartésienne.

Équation canonique ou segmentaire du plan

La formule de l’équation canonique ou segmentaire d’un plan est la suivante :

Où:

• C’est le point d’intersection entre le plan et l’axe X.
• C’est le point d’intersection entre le plan et l’axe Y.
• C’est l’endroit où le plan coupe l’axe Z.

Vecteur normal à un plan

Le vecteur normal à un plan est un vecteur perpendiculaire à toutes les lignes contenues dans ce plan. Par conséquent, un vecteur normal à un plan signifie qu’il est perpendiculaire au plan.

De nombreux problèmes métriques en géométrie analytique dans l’espace concernent les plans et leurs vecteurs normaux. Pour résoudre ces exercices il vous suffit de connaître la relation mathématique entre un plan et son vecteur normal :

Les composantes X, Y, Z du vecteur normal à un plan coïncident respectivement avec les coefficients A, B, C de l’équation implicite (ou générale) dudit plan.

Où

est le vecteur orthogonal au plan

Positions relatives de deux éléments géométriques dans l’espace

Évidemment, une ligne ou un plan ne doit pas nécessairement être seul dans l’espace, mais bien au contraire, ils interagissent normalement les uns avec les autres : ils se coupent, sont parallèles, perpendiculaires, etc. Eh bien, dans cette section, nous verrons les différentes positions relatives des lignes et des plans et comment elles sont déterminées.

Position relative de deux lignes dans l’espace

En géométrie analytique, lorsque l’on travaille dans un espace tridimensionnel (en R3) il y a 4 positions relatives possibles entre deux droites : deux droites peuvent être des droites coïncidentes , des droites parallèles , des droites sécantes ou des droites sécantes .

Comment trouver la position relative de deux lignes par plages

Une façon de trouver la position relative de deux lignes consiste à calculer les plages de deux matrices spécifiques, comme nous le verrons ci-dessous. Cette méthode est très utile lorsque les deux droites sont exprimées sous la forme d’une équation implicite (ou générale).

Ainsi, si l’on a deux droites exprimées avec leurs équations implicites (ou générales) dans un espace tridimensionnel (en R3) :

Soit A la matrice composée des coefficients des deux droites :

Et étant donné la matrice développée A’, qui est la matrice formée de tous les paramètres des deux droites :

Ensuite, la position relative des deux lignes peut être déterminée par l’étendue des deux matrices précédentes selon le tableau suivant :

Par conséquent, pour trouver la position relative entre deux lignes, nous devrons calculer les plages des deux matrices et en fonction de la plage de chaque matrice, ce sera un cas ou un autre.

Ce théorème peut être prouvé à partir du théorème de Rouché-Frobenius (une méthode utilisée pour résoudre des systèmes d’équations linéaires), cependant sur cette page nous ne ferons pas la preuve car elle est assez lourde et n’apporte pas grand-chose.

Position relative de deux avions dans l’espace

En géométrie analytique, il n’existe que trois positions relatives possibles entre deux plans : les plans sécants, les plans parallèles et les plans coïncidants.

• Plans sécants : deux plans sont sécants s’ils ne se coupent que sur une ligne.
• Plans parallèles : Deux plans sont parallèles s’ils ne se coupent en aucun point.
• Plans coïncidents : deux plans sont coïncidents s’ils ont tous les points en commun.

Comment déterminer la position relative de deux avions par des coefficients

Une façon de connaître la position relative entre deux plans consiste à utiliser les coefficients de leurs équations générales (ou implicites).

Soit alors l’équation générale (ou implicite) de deux plans différents :

La position relative entre les deux plans dans un espace tridimensionnel dépend de la proportionnalité de leurs coefficients ou paramètres :

Ainsi, les deux plans seront sécants lorsque l’un des coefficients A, B ou C n’est pas proportionnel aux autres. En revanche, les deux plans seront parallèles lorsque seuls les termes indépendants ne seront pas proportionnels. Et enfin, les plans coïncideront lorsque tous les coefficients des deux équations seront proportionnels.

Distances dans l’espace

Ci-dessous vous avez les formules pour calculer la distance entre différents éléments géométriques : entre un point et une droite, entre deux plans, entre un plan et une droite,…

Distance entre deux points

La distance entre deux points correspond à la norme du vecteur déterminé par ces 2 points.

Donc si on a deux points génériques :

La formule de la distance entre les deux points est :

Distance d’un point à une ligne

La formule pour calculer la distance d’un point à une ligne dans l’espace est la suivante :

Où:

• est le module du vecteur directeur de la droite
• est un point sur la droite un point sur la ligne et le vecteur défini par les deux points
• est le module du produit vectoriel entre les vecteurs et

Distance entre deux lignes

La distance entre deux lignes dépend de leur position relative :

• Si les deux lignes coïncident ou se coupent , la distance entre les deux lignes est égale à zéro, puisqu’elles se coupent (au moins) en un point.
• Lorsque les deux droites sont parallèles ou se coupent, il faut appliquer une formule selon les cas (les deux explications sont disponibles ci-dessous).

Distance entre deux lignes parallèles

Deux lignes parallèles sont toujours à la même distance l’une de l’autre. Donc pour calculer la distance entre deux droites parallèles dans l’espace (dans R3) cela se fait de la même manière que dans le plan (dans R2) : il suffit de prendre un point sur l’une des deux droites et de trouver la distance qu’il y a est de ce point à l’autre ligne.

Donc pour déterminer la distance entre 2 droites parallèles vous devez utiliser la formule de la distance entre un point et une droite.

Distance entre deux lignes qui se croisent

Soit le vecteur directeur et tout point de deux droites sécantes :

La formule de la distance entre deux lignes qui se croisent est :

Où:

• est la valeur absolue du produit mixte des vecteurs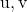 et le vecteur défini par les points et .
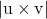• est le module du produit vectoriel entre les vecteurs directeurs des deux lignes croisées.

Bien que vous ayez la formule ici, déterminer la distance entre deux lignes qui se croisent est plus compliqué qu’il n’y paraît. Donc, si vous souhaitez vous entraîner dans le lien suivant, vous pouvez voir des exemples et des exercices résolus sur la distance entre deux lignes qui se croisent.

Distance d’un point à un plan

Étant donné un point et l’équation générale (ou implicite) d’un plan :

La formule de la distance d’un point à un plan est :

Si en appliquant la formule nous obtenons un résultat égal à zéro, cela signifie évidemment que la distance entre le point et le plan est nulle et, par conséquent, le point fait partie de ce plan.

Distance entre deux plans

La distance entre deux plans dans l’espace dépend de la position relative entre ces deux plans :

• Si les deux plans sont sécants ou coïncidents , la distance qui les sépare est égale à zéro car ils se coupent en un certain point.
• Si les deux plans sont parallèles , la distance entre les deux plans est calculée en prenant un point sur l’un des deux plans et en calculant la distance entre ce point et l’autre plan.

Distance entre deux plans parallèles

Deux plans parallèles sont toujours à la même distance l’un de l’autre, donc pour trouver la distance entre deux plans parallèles, nous pouvons prendre un point sur l’un des deux plans et calculer la distance de ce point à l’autre plan.

Donc pour calculer la distance entre deux plans parallèles vous devez trouver un point sur l’un des deux plans puis utiliser la formule de la distance entre un point et un plan.

Angles dans l’espace

Comme pour les distances, la détermination de l’angle entre deux objets géométriques dans l’espace dépend de leurs caractéristiques géométriques. Car calculer l’angle formé par deux droites n’est pas la même chose que calculer l’angle formé par deux plans. Vous avez donc ci-dessous les formules pour trouver les angles entre les lignes et les plans.

Angle entre deux lignes

Pour connaître l’angle entre deux droites dans l’espace euclidien, il faut calculer l’angle formé par leurs vecteurs directeurs, donc :

Étant donné les vecteurs directeurs de deux lignes différentes :

L’ angle formé par ces deux droites peut être calculé avec la formule suivante :

Où

et sont les modules des vecteurs et respectivement.

Rappelons que la formule du module d’un vecteur est :

Angle entre deux plans

L’angle entre deux plans est égal à l’angle formé par les vecteurs normaux desdits plans. Par conséquent, pour trouver l’angle entre deux plans, on calcule l’angle formé par leurs vecteurs normaux, puisqu’ils sont équivalents .

Étant donné l’équation générale (ou implicite) de deux plans différents :

Le vecteur normal de chaque plan est :

Et l’angle formé par ces deux plans est déterminé en calculant l’angle formé par leurs vecteurs normaux à l’aide de la formule suivante :

Angle entre une ligne et un plan

L’angle formé par une droite et un plan est défini comme le plus petit des deux angles complémentaires formés par le vecteur directeur de la droite et le vecteur normal du plan.

Par conséquent, si

est le vecteur directeur de la droite et est le vecteur normal au plan :

La formule utilisée pour calculer l’angle formé par une droite et un plan est :