Cette page explique la signification du point médian d’un segment. De plus, vous découvrirez comment trouver le milieu d’un segment grâce à sa formule. Vous pourrez même voir des exemples, des exercices et des problèmes résolus de points médians de segments.
Quel est le milieu d’un segment ?
En mathématiques, le milieu d’un segment est le point situé à la même distance des extrémités d’un segment. Le milieu divise donc le segment en deux parties égales.
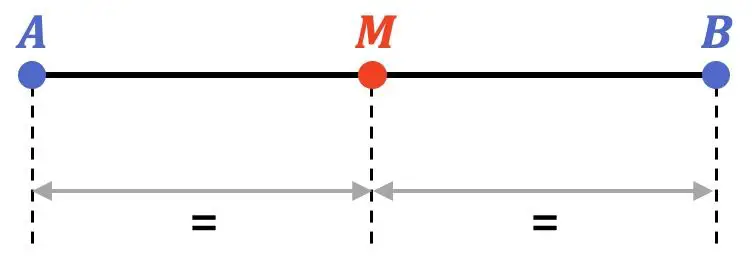
De plus, le milieu est en plein centre du segment, il appartient donc à la bissectrice du segment.
D’autre part, le milieu d’un segment est aussi un point équidistant de deux éléments géométriques : les deux extrémités du segment.
Comment calculer le milieu d’un segment ?
Étant donné les coordonnées cartésiennes des points extrêmes d’un segment :
![]()
Les coordonnées du milieu dudit segment correspondent à la demi-somme des coordonnées des points extrêmes :
![]()
C’est la formule du milieu d’un segment dans le plan cartésien (dans R2). Mais évidemment la formule est aussi applicable à l’espace cartésien (dans R3), il suffit d’ajouter la demi-somme de la coordonnée Z :
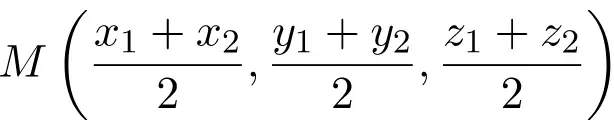
Regardons un exemple de la façon de calculer les coordonnées du milieu d’un segment :
- Déterminez le milieu du segment formé par les points suivants :
![]()
Pour trouver le milieu du segment, il suffit d’appliquer sa formule :
![]()
![]()
![]()
![]()
Exercices résolus au milieu d’un segment
Exercice 1
Quel est le milieu du segment dont les extrémités sont les deux points suivants ?
![]()
Pour connaître le milieu du segment il faut appliquer directement la formule :
![]()
![]()
![]()
![]()
Exercice 2
Trouvez les coordonnées de l’extrémité finale du segment qui commence au point A et dont le milieu est M.
![]()
Dans ce cas on connaît les coordonnées du point initial et du milieu du segment. Par conséquent, nous substituons les coordonnées que nous connaissons dans la formule du milieu d’un segment :
![]()
![]()
Et maintenant, nous résolvons les coordonnées du point final du segment à partir de l’équation précédente :
Coordonnée X
![]()
![]()
![]()
![]()
![]()
Coordonnée Y
![]()
![]()
![]()
![]()
![]()
Les coordonnées de la fin finale du segment sont donc :
![]()
Exercice 3
Étant donné le parallélogramme suivant :
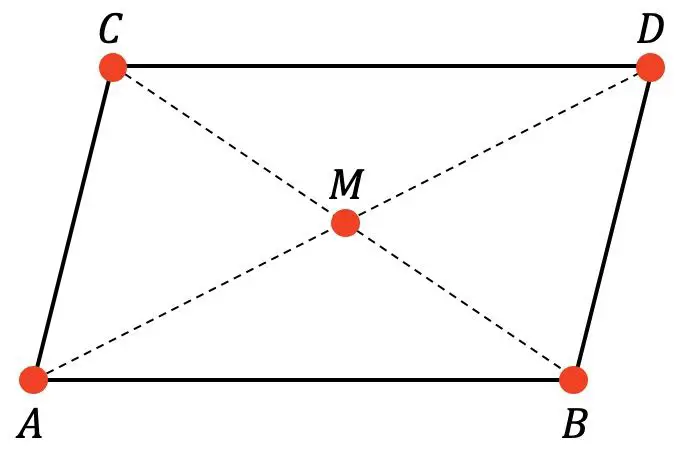
On sait que M est le centre du parallélogramme et les coordonnées des points A, B et C sont :
![]()
À partir de ces informations et en utilisant la formule du point milieu, calculez les coordonnées du point D.
Pour trouver les coordonnées du point D à l’aide de la formule du milieu d’un segment, il faut d’abord calculer les coordonnées du point M puis celles du point D.
Le point M est le milieu du segment BC, ses coordonnées sont donc :
![]()
![]()
Et une fois que l’on connaît le point M, on peut trouver le point D. Le point M est aussi le milieu du segment AD, donc :
![]()
Coordonnée X du point D
![]()
![]()
![]()
Coordonnée Y du point D
![]()
![]()
![]()
Les coordonnées du point D sont donc :
![]()
Exercice 4
Calculez l’équation continue de la droite perpendiculaire au segment PQ en son milieu. Être les points
![]() et
et ![]()
Pour déterminer l’équation d’une droite, nous avons besoin de son vecteur directeur et d’un point qui fait partie de la droite.
Dans ce cas, le vecteur directeur de la droite sera perpendiculaire au vecteur
![]() On calcule donc le vecteur
On calcule donc le vecteur ![]()
![]()
Et on peut trouver un vecteur perpendiculaire à un autre en changeant les composantes du vecteur entre elles puis en changeant le signe d’une composante, donc :
![]()
Nous avons maintenant le vecteur directeur de la ligne, nous n’avons donc besoin que d’un seul point appartenant à la ligne. Dans ce cas, l’instruction nous indique que la ligne passe par le milieu du segment, nous calculons donc le milieu à l’aide de la formule :
![]()
![]()
Enfin, nous construisons l’équation continue de la droite à partir du point et du vecteur calculés :
![]()