Les fractions ou nombres fractionnaires sont un concept mathématique très important dans le domaine du calcul. Par conséquent, il est essentiel de savoir comment ils fonctionnent et de savoir comment résoudre des exercices de fractions . C’est l’objectif de cet article, que vous appreniez à résoudre des opérations avec des fractions et tout autre type d’exercice ou de problème qui comprend des nombres de ce style. Cela dit, commençons par les premiers exercices.
Exercice sur les opérations avec les fractions
Pour commencer, nous proposons quelques opérations de base qui incluent des fractions, il vous suffit de les résoudre et d’exprimer le résultat simplifié. Ainsi, une fois que vous avez fini de résoudre les calculs , nous vous recommandons de comparer les résultats et de regarder la correction que nous vous proposons. Bien que vous puissiez également vérifier vos résultats avec notre calculateur de fractions en ligne.
Addition et soustraction de fractions avec un dénominateur commun
Ci-dessous, vous avez deux additions et deux soustractions de fractions résolues, essayez de les résoudre par vous-même et comparez le résultat. De cette manière, vous passerez en revue les mécanismes de résolution de ce type d’opération :
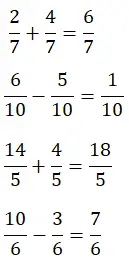
Addition et soustraction de fractions avec différents dénominateurs
Maintenant, nous élevons un peu le niveau, car pour résoudre l’addition et la soustraction de fractions avec des dénominateurs différents, nous devons d’abord trouver le lcm des dénominateurs. Le calcul se complique donc un peu.
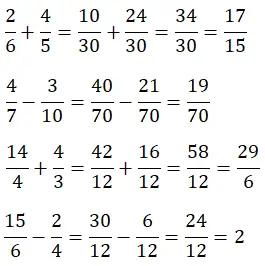
Multiplication et division de fractions
Dans cette section, vous devrez résoudre la multiplication et la division de fractions, ces opérations sont très faciles à faire, mais encore faut-il les pratiquer. Comme dans les deux sections précédentes, vous en avez deux de chaque type.
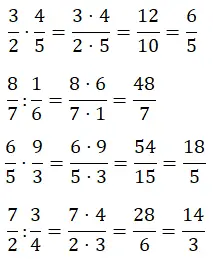
fractions combinées
Enfin, vous allez devoir résoudre des fractions combinées , qui sont des opérations combinées avec des fractions. L’élément le plus compliqué de ceux-ci est le calcul, puisque vous devez rassembler toutes vos connaissances sur les opérations avec des nombres fractionnaires pour pouvoir résoudre correctement un calcul de ce type.

Exercice de conversions entre décimales et fractions
Vous devriez maintenant essayer de convertir les nombres décimaux suivants en une fraction génératrice et vice versa. Bien que pour le faire correctement, vous devez tenir compte du type de décimal (exact, périodique pur ou périodique mixte), car les méthodes de conversion varient. Si vous ne vous souvenez pas de ces méthodes, nous vous recommandons de lire notre article sur les fractions , car nous y expliquons toutes les procédures de conversion entre décimales et fractions et vice versa. Ci-dessous, vous pouvez trouver quelques conversions résolues, nous vous recommandons d’essayer de les faire vous-même :

Exercice sur les fractions équivalentes
Après avoir pratiqué l’arithmétique de base et les conversions, il est temps de commencer avec les fractions équivalentes . Dans cette section, nous allons vous montrer plusieurs fractions et vous devrez trouver les paires de fractions équivalentes. De cette façon, vous pratiquerez le concept d’équivalence et réviserez égalementles fractions simplificatrices .

Exercice de comparaison de fractions
Ensuite, nous allons vous montrer plusieurs fractions et vous devrez les comparer avec les symboles «<«, «=» et «>». Afin de résoudre cet exercice, vous devrez trouver un dénominateur commun et convertir les deux fractions en ce dénominateur. De cette façon, vous pourrez voir lequel des deux numérateurs est le plus grand, et vous devez agir en conséquence :

Exercice sur les fractions sur la droite numérique
Dans cet exercice vous allez devoir ordonner les différentes fractions que nous allons vous donner sur une droite numérique , ainsi la procédure de résolution peut être assez variée. Par exemple, vous pouvez diviser la distance entre deux nombres entiers par autant de parties qu’indiqué par la valeur du dénominateur, puis placer la fraction dans le segment indiqué par le numérateur .
De plus, vous pouvez diviser le numérateur par le dénominateur et obtenir un nombre décimal, que vous placerez plus tard sur la ligne. Bien que cette deuxième procédure soit beaucoup plus basique , c’est pour cela que nous avons choisi de choisir la première méthode que nous avons expliquée. Ceci étant dit, les fractions que vous devrez placer sur la droite sont les suivantes :
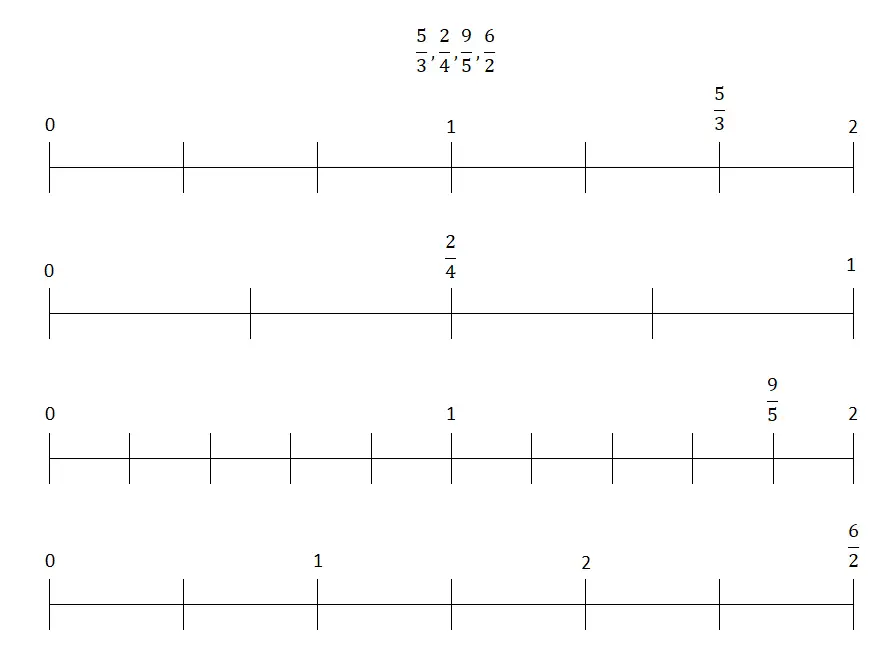
problèmes de fraction
Enfin, nous arrivons à la dernière partie de cet article, dans laquelle nous traiterons quelques problèmes de fractions. Bien que tout d’abord, nous souhaitons décrire la procédure correcte que vous devez utiliser lors de la résolution de problèmes mathématiques :
- Comprendre le problème : la première étape consiste à faire une bonne lecture, grâce à laquelle vous comprenez l’ensemble du problème. De cette façon, vous vous familiariserez avec toutes les informations expliquées dans la déclaration. Si vous faites cette partie correctement, alors vous avez beaucoup fait, puisque vous saurez comment router la résolution et tous les calculs.
- Énoncé du problème : une fois que vous savez en quoi consiste le problème, vous devrez le présenter. Vous pouvez le faire au moyen d’un diagramme, d’un dessin ou d’une petite représentation graphique des données. Dans cette étape, vous commencerez à réfléchir aux moyens de connecter les données et de résoudre le problème.
- Résoudre le problème lui-même : plus tard, vous pouvez continuer à résoudre le problème numériquement, dans cette phase, vous devez tester les théories que vous avez soulevées dans la section précédente. C’est à cette étape que vous exécutez réellement un plan d’action et obtenez les résultats, vous devez donc être très concentré.
- Interpréter les solutions : enfin, lorsque vous avez déjà les solutions, vous devrez interpréter ces résultats et leur donner un sens dans le contexte du problème. Cette dernière étape est très importante et beaucoup de gens l’ignorent, car ils pensent qu’un résultat numérique suffit, mais en réalité il faut résumer la solution en une phrase.
problème 1
Si nous voulons remplir une piscine avec un robinet, cela prend 6 heures, mais si nous le faisons avec un autre robinet, cela prend 8 heures. Quelle quantité de la piscine sera remplie en 2 heures si nous utilisons les deux robinets en même temps ? Exprimer le résultat sous forme de fraction.
Pour résoudre ce problème, nous devons recourir aux fractions. Fondamentalement, ce que nous allons faire est de calculer séparément combien chaque robinet remplira pendant ces deux heures. Ainsi, le premier robinet remplira 1/6 du réservoir en une heure et si on le multiplie par deux heures, il remplira 2/6. Alors que le deuxième robinet remplira 1/8 en une heure et nous devrons également le multiplier par 2, avec lequel nous aurons 2/8.
Enfin, nous ajouterons les deux fractions, pour obtenir le montant total de la piscine qui aura été rempli. Il nous reste donc 2/6 + 2/8 = 7/12 du pool.
problème 2
Nous avons 64 bonbons, mais nous en donnons 1/4 à notre ami Marcos. Ensuite, nous mangeons 3 bonbons et donnons 2/5 du montant restant à notre amie María. Combien nous reste-t-il de bonbons ? Exprimez-le sous la forme d’un nombre entier.
Premièrement, nous devons soustraire un quart du montant total de 64, puis nous soustrairons 3 du résultat obtenu et enfin nous soustrairons les deux cinquièmes de cette somme de bonbons. Avec lequel, nous pouvons calculer cela avec des fractions combinées :
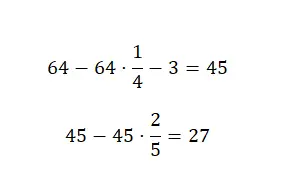
Par conséquent, à la fin, il nous reste 27 bonbons.
problème 3
Nous avons un terrain de 10 000 m² divisé en trois parties inégales. La première section représente les 3/6 de la superficie totale et la deuxième section est égale à la moitié de la précédente. Quelle fraction décrit l’aire de la troisième section? Combien de mètres carrés compte chaque secteur ?
La première chose que nous ferons est de calculer la fraction de la troisième parcelle, nous le ferons au moyen d’une soustraction très simple de fractions. Ensuite, nous allons calculer la surface de chaque section en calculant la fraction d’un nombre, dans notre cas cette valeur numérique sera de 10 000. Ci-dessous, vous pouvez voir toute la procédure :