Sur cette page, nous expliquons ce qu’est le produit mixte de trois vecteurs (ou triple produit scalaire) et comment il est calculé. Vous verrez également des exemples, des exercices et des problèmes résolus sur ce type d’opération entre vecteurs. Et, en plus, vous trouverez les propriétés et les applications du produit mélangé.
Quel est le produit mixte de trois vecteurs ?
Le produit mixte de trois vecteurs, également appelé triple produit scalaire , est une multiplication successive entre trois vecteurs impliquant deux types d’opérations différentes : le produit scalaire et le produit vectoriel . Ainsi, la combinaison des deux opérations vectorielles donne un scalaire (un nombre réel).
Concrètement, le produit mixte consiste à calculer le produit vectoriel de deux vecteurs et, ultérieurement, à multiplier vectoriellement le résultat obtenu par un troisième vecteur. Ecrit comme cela cela peut sembler très compliqué, mais en réalité ce n’est pas tant que ça, regardez la formule du triple produit scalaire :
![]()
Comme vous pouvez le voir dans sa formule, le produit mixte de trois vecteurs est indiqué par deux crochets.
Comment calculer le produit mixte de trois vecteurs ?
La formule du triple produit scalaire est celle que nous venons de voir dans la section précédente, cependant, elle n’est généralement pas utilisée pour déterminer le produit mixte de trois vecteurs car il existe un autre moyen, plus simple et plus rapide :
Soit 3 vecteurs quelconques :
![]()
Pour calculer le produit mixte entre trois vecteurs, il suffit de résoudre le déterminant 3×3 formé par les composantes des vecteurs :
![Rendered by QuickLaTeX.com \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]=\begin{vmatrix} \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \\[1.1ex] \text{w}_x & \text{w}_y & \text{w}_z \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a3fed933d4d02bb5ca6f5bae06ea544d_l3.png)
Pour que vous puissiez voir un exemple de comment est calculé , nous allons trouver le produit mixte des trois vecteurs suivants :
![]()
Pour déterminer le produit mixte, on construit un déterminant d’ordre 3 en plaçant les vecteurs en lignes de la matrice :
![Rendered by QuickLaTeX.com \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]=\begin{vmatrix} 1 & 2 & 0 \\[1.1ex] 0 & -1 & 3 \\[1.1ex] -2 & 4 & 1 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e5341b4a39b42c1284a4b0129b38b61a_l3.png)
Et maintenant, il ne nous reste plus qu’à résoudre le déterminant de la matrice, pour cela, vous pouvez utiliser n’importe quelle méthode. Dans ce cas, on appliquera la règle de Sarrus (mais cela peut aussi se faire par adjonctions ou cofacteurs) :
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 1 & 2 & 0 \\[1.1ex] 0 & -1 & 3 \\[1.1ex] -2 & 4 & 1 \end{vmatrix} \\[2ex] &= -1-12+0-0-12-0 \\[2ex] & = \bm{-25} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-df86565048cf897265878936f2294525_l3.png)
Pour montrer que les deux procédures sont équivalentes, nous allons calculer le produit mixte des mêmes vecteurs au moyen de leur définition :
![Rendered by QuickLaTeX.com \begin{aligned} \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] & = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}})\\[2ex] &=(1,2,0) \cdot \Bigl( (0,-1,3)\times (-2,4,1)\Bigr) \\[2ex] & = (1,2,0) \cdot \begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 0& -1 & 3 \\[1.1ex] -2 &4&1 \end{vmatrix} \\[2ex] &= (1,2,0) \cdot (-13,-6,-2) \\[2ex] & = \bm{-25} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e4d15d610ca9b4cb39e9f268cfb152ae_l3.png)
Nous vous recommandons de calculer le produit mixte à travers le déterminant des vecteurs, car c’est plus rapide et il y a moins de chances de faire des erreurs. Mais, comme vous pouvez le voir, le résultat est le même quelle que soit la méthode que vous utilisez, alors utilisez celle que vous préférez. 👍
Interprétation géométrique du produit mélangé
Une fois que vous savez comment trouver le produit mixte de trois vecteurs, vous vous demandez peut-être… et à quoi sert le produit mixte ? Eh bien, en mathématiques, il a deux utilisations principales : calculer le volume d’un parallélépipède et le volume d’un tétraèdre.
Le volume d’un parallélépipède est égal à la valeur absolue du produit mixte des vecteurs qui marquent les 3 dimensions du champ géométrique.
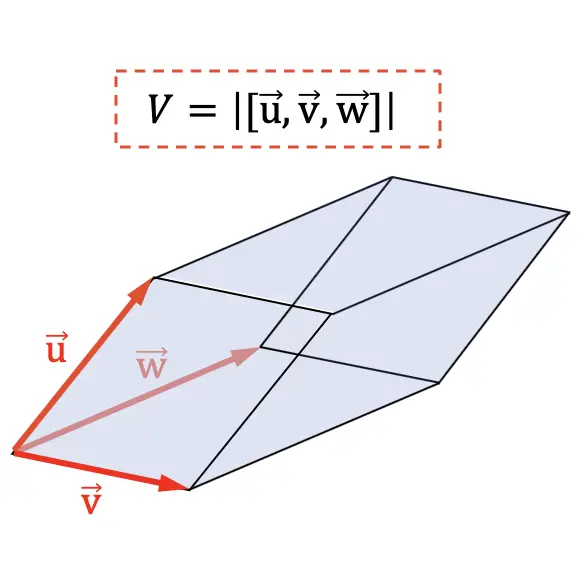
Une autre application du produit mixte est de déterminer le volume d’un tétraèdre . Puisque géométriquement la sixième partie de la valeur absolue du produit mixte représente le volume d’un tétraèdre :
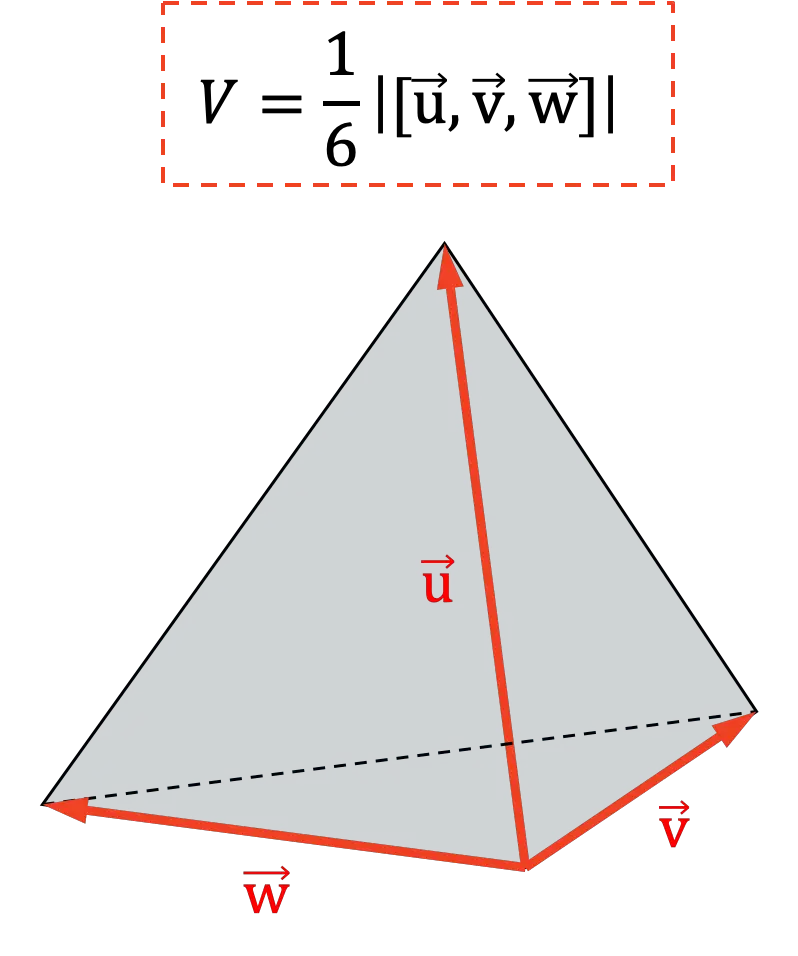
Propriétés du produit mixte ou triple produit scalaire
Le produit mixte, ou triple produit scalaire, a les caractéristiques suivantes :
- En général, un changement dans l’ ordre des vecteurs de produits mixtes implique également un changement de signe. Par conséquent, l’ordre des vecteurs de produits mixtes est important.
![]()
- Cependant, si nous modifions l’ordre de manière cyclique , le signe ne change pas :
![]()
- Dans un espace à trois dimensions (dans R3), le produit mixte de trois vecteurs linéairement dépendants ou coplanaires (appartenant au même plan) est égal à 0.
Problèmes résolus de produits mélangés
Exercice 1
Étant donné 3 vecteurs :
![]()
Calculez le produit mixte des trois vecteurs :
![]()
Pour trouver son produit mixte, il faut résoudre le déterminant composé des coordonnées des vecteurs :
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 3 & -1 & 2 \\[1.1ex] -2 & 0 & 1 \\[1.1ex] 5 & 1 & -1 \end{vmatrix} \\[2ex] &= 0-5-4-0-3+2 \\[2ex] & = \bm{-10} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-549ed90889d541ae4a1075449567b062_l3.png)
Exercice 2
Étant donné 3 vecteurs :
![]()
Déterminez le produit mixte entre les trois vecteurs :
![]()
Pour trouver son produit mixte, nous devons résoudre le déterminant qui a les coordonnées cartésiennes des vecteurs sous forme de lignes :
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 7 & 2 & -3 \\[1.1ex] 2 & 4 & 9 \\[1.1ex] 4 & 3 & -1 \end{vmatrix} \\[2ex] &= -28+72-18+48-189+4 \\[2ex] & = \bm{-111} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-29b46155243552a99f6fd75de69f59da_l3.png)
Exercice 3
Calculer le volume du parallélépipède dont les 3 côtés sont les vecteurs suivants :
![]()
Le volume d’un parallélépipède est égal à la valeur absolue du produit mixte de 3 des vecteurs qu’il a pour arêtes. Par conséquent, nous calculons d’abord le triple produit croisé des vecteurs :
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 0 & 2 & 5 \\[1.1ex] -1 & 6 & 2 \\[1.1ex] 3 & 1 & 2 \end{vmatrix} \\[2ex] &= 0+12-5-90-0+4 \\[2ex] & = -79 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9718b369a508216fbb69ab68ac7de381_l3.png)
Pour que le volume du parallélépipède soit la valeur absolue du résultat du produit mixte :
![]()
Exercice 4
Calculez le volume du tétraèdre qui a pour sommets les points suivants :
![]()
Tout d’abord, nous calculons les vecteurs qui représentent les arêtes du tétraèdre :
![]()
![]()
![]()
Le volume d’un tétraèdre équivaut à un sixième de la valeur absolue du produit mixte de 3 des vecteurs qu’il a pour les arêtes. Par conséquent, nous calculons d’abord le produit mixte des vecteurs trouvés :
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 2 & 3 & 0 \\[1.1ex] 4 & -1 & 2 \\[1.1ex] 3 & 2 & -1 \end{vmatrix} \\[2ex] &= 2+18+0-0-8+12 \\[2ex] & = 24 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d384e76415a756b834e0a8e7c695b1c1_l3.png)
Ainsi le volume du tétraèdre sera un sixième de la valeur absolue du produit mixte :
![]()