Sur cette page vous trouverez la signification de l’excentricité de l’ellipse et comment elle est calculée (formule). De plus, vous verrez des exemples de calculs d’excentricités d’ellipses.
Quelle est l’excentricité de l’ellipse ?
L’excentricité de l’ellipse est un paramètre qui mesure à quel point une ellipse est ronde ou aplatie, c’est-à-dire que l’excentricité d’une ellipse indique à quel point l’ellipse ressemble à un cercle.
D’autre part, rappelons aussi en quoi consiste une ellipse : l’ellipse est le lieu de tous les points d’un plan dont la somme des distances à deux autres points fixes (appelés foyers F et F’) est constante.
Formule d’excentricité d’ellipse
Une fois que nous avons vu la définition de l’excentricité de l’ellipse, voyons comment elle est calculée à partir de sa formule :
La formule de l’excentricité de l’ellipse est la suivante :
Où:
est l’excentricité de l’ellipse
est la distance d’un foyer (points F et F’) de l’ellipse à son centre
est la longueur du demi-grand (ou grand) axe de l’ellipse.
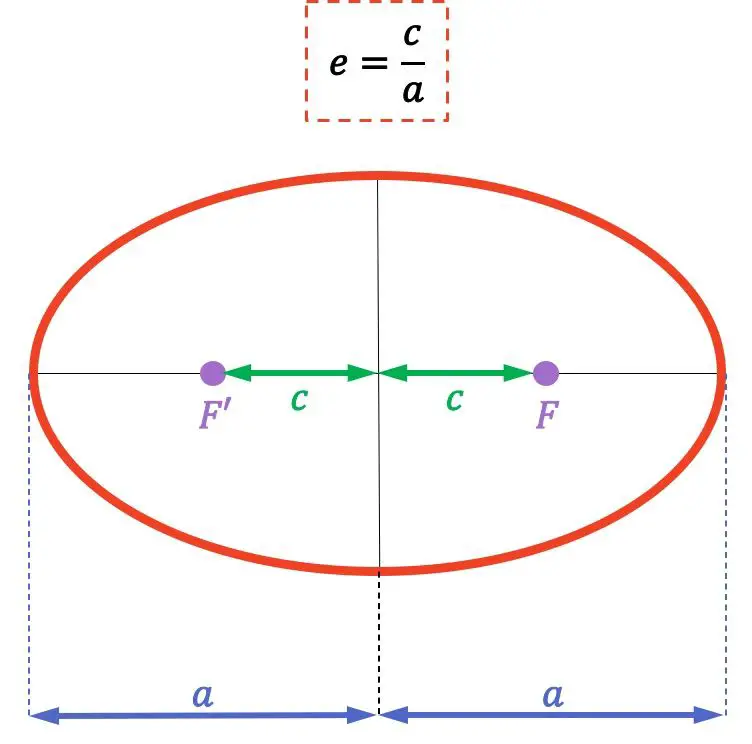
Rappelez-vous que les foyers d’une ellipse sont les points fixes dont la somme des distances à tout point de l’ellipse est constante. De plus, la distance entre les deux foyers s’appelle la distance focale.
La valeur de l’excentricité va de zéro, ce qui signifie qu’il s’agit d’un cercle parfait, à un, ce qui implique qu’il s’agit d’une droite horizontale. De toute évidence, 0 et 1 ne sont pas inclus car les objets géométriques résultants ne sont plus des ellipses.
d(P,F) + d(P,F’)= 2a 
d(P,F)
d(P,F’)
a
a
a^2=b^2+c^2 
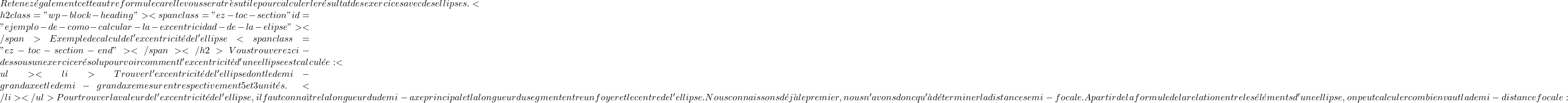a^2=b^2+c^2 c^2=a^2-b^2 c=\sqrt{a^2-b^2} = \sqrt{5^2-3^2}=\sqrt{16} = 4 
ac,
e= \cfrac{c}{a} = \cfrac{4}{5} = \bm{0,8} $