L’erreur absolue et l’erreur relative sont deux mesures utilisées pour évaluer la précision d’un calcul ou d’une estimation.
L’erreur absolue fait référence à la différence entre la valeur réelle et la valeur estimée . Pour sa part, l’erreur relative fait référence au rapport entre l’erreur absolue et la valeur réelle.
Les deux sont importants car ils fournissent des informations sur l’exactitude et la pertinence des résultats. De plus, ils sont largement utilisés dans de nombreux domaines, notamment l’ingénierie, la physique et l’économie. Nous décrivons chacun ci-dessous.
Quelle est l’erreur absolue ?
L’erreur absolue est une mesure de la différence entre une valeur mesurée ou estimée et la valeur réelle.
Elle est représentée par la formule : |valeur mesurée – valeur réelle| . En d’autres termes, l’erreur absolue est la valeur absolue de la différence entre les valeurs mesurées ou estimées et les valeurs réelles.
Exprimé en langage mathématique, il reste comme suit :
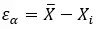
Il convient de mentionner qu’il s’agit d’une mesure fondamentale dans de nombreux domaines, tels que la science, la technologie, l’ingénierie et l’économie, car elle permet d’évaluer la précision des résultats et la qualité des modèles et des estimations.
Comment l’erreur absolue est-elle calculée ?
Le calcul de l’erreur absolue est simple :
La valeur mesurée ou estimée est soustraite de la valeur réelle et la valeur absolue du résultat est prise.
Par exemple, si la valeur réelle est 10 et la valeur mesurée ou estimée est 9, l’erreur absolue serait :
|9 – 10| = |-1| = 1.
Autre exemple, si la valeur réelle est 15 et la valeur mesurée ou estimée est 17, l’erreur absolue serait :
|17 – 15| = |2| = 2.
Vous pouvez également calculer l’ erreur absolue moyenne , qui correspond à la somme totale des erreurs absolues divisée par le nombre de mesures ou d’estimations. Pour le calculer, il faut suivre la formule suivante :
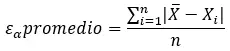
Ceci est utile lorsque vous avez de nombreuses mesures ou estimations et que vous souhaitez avoir une idée générale de la précision des résultats.
Supposons que nous ayons les mesures ou estimations suivantes :
Valeur réelle : 20
Valeur mesurée 1 : 18
Valeur mesurée 2 : 22
Valeur mesurée 3 : 19
Nous calculons l’erreur absolue pour chaque mesure comme suit :
Erreur absolue 1 : |18 – 20| = 2
Erreur absolue 2 : |22 – 20| = 2
Erreur absolue 3 : |19 – 20| = 1
Nous calculons l’erreur absolue moyenne comme suit : (2 + 2 + 1) ÷ 3 = 1,67. Cela indique qu’en moyenne, les mesures ou les estimations sont à 1,67 unités de la valeur réelle.
Quelle est l’erreur relative ?
L’erreur relative est une mesure de la précision d’une mesure ou d’une estimation en termes de rapport entre l’erreur absolue et la valeur réelle.
Elle est représentée par la formule : (erreur absolue) ÷ (valeur réelle) . Exprimé en langage mathématique, il reste comme suit :
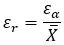
L’erreur relative est utile pour comparer la précision de différentes mesures ou estimations, en particulier lorsque les valeurs réelles sont différentes.
Comment l’erreur relative est-elle calculée ?
Lors du calcul de l’erreur relative, l’erreur absolue est normalisée de manière à ce que la précision de différentes mesures ou estimations puisse être comparée indépendamment de leurs valeurs réelles.
Par exemple, supposons que vous ayez deux mesures ou estimations, A et B, avec des valeurs vraies de 10 et 100, respectivement, et des erreurs absolues de 1 et 5, respectivement.
L’erreur relative pour la mesure A serait (1) ÷ (10) = (0,1), tandis que l’erreur relative pour la mesure B serait (5) ÷ (100) = (0,05). Cela indique que la mesure B est plus précise que la mesure A en termes relatifs, même si elle a une erreur absolue plus grande.
Voici quelques exemples de la façon dont l’erreur relative peut être calculée :
1. Mesurer la hauteur d’un bâtiment et on estime qu’il mesure 100 mètres :
Après avoir pris la mesure, on découvre qu’il mesure en réalité 98 mètres de long.
L’erreur absolue serait de 2 mètres et l’erreur relative serait de (2) ÷ (98) = 0,0204 ou 2,04 %.
2. Supposons que vous vouliez mesurer le poids d’un objet et que vous estimiez qu’il pèse 10 kilogrammes.
Après avoir pris la mesure, on découvre qu’il pèse en fait 9,5 kilogrammes.
L’erreur absolue serait de 0,5 kilogramme et l’erreur relative serait de (0,5) ÷ (9,5) = 0,0526 ou 5,26 %.
3. Supposons que vous souhaitiez mesurer la longueur d’une planche et que l’on estime qu’elle mesure 200 centimètres.
Après avoir effectué la mesure, on découvre qu’il s’agit en réalité de 201 centimètres.
L’erreur absolue serait de 1 centimètre et l’erreur relative serait de (1) ÷ (201) = 0,00498 ou 0,498 %.
Dans chacun de ces exemples, l’erreur relative fournit une mesure de la précision de la mesure en termes de rapport de l’erreur absolue à la valeur vraie. Cela vous permet de comparer la précision de différentes mesures et estimations, quelles que soient leurs valeurs réelles.
Quelle est la différence entre erreur absolue et erreur relative ?
L’erreur absolue et l’erreur relative sont deux mesures différentes pour évaluer l’exactitude d’un résultat ou d’un modèle.
L’erreur absolue fait référence à la différence entre la valeur réelle ou vraie d’une quantité et la valeur estimée ou mesurée. Elle peut être calculée comme la différence entre la valeur réelle et la valeur estimée :
Erreur absolue = valeur réelle – valeur estimée
L’erreur absolue peut être positive ou négative , selon que la valeur estimée est supérieure ou inférieure à la valeur réelle.
D’autre part, l’erreur relative fait référence à la relation entre l’erreur absolue et la valeur réelle ou vraie . Il peut être calculé comme la fraction de l’erreur absolue et de la valeur réelle :
Erreur relative = erreur absolue ÷ valeur réelle
L’erreur relative est généralement exprimée en pourcentage . Ce type d’erreur permet de comparer la précision de différents résultats ou modèles, quelle que soit leur ampleur.
Par exemple, une erreur absolue de 1,0 peut être un écart significatif d’une petite quantité, mais pas d’une grande quantité. Cependant, l’erreur relative dans les deux cas sera la même.
En bref, l’erreur absolue mesure la différence entre la valeur réelle et la valeur estimée, tandis que l’erreur relative mesure la précision de l’estimation en termes de relation avec la valeur réelle.
Quelles sont les applications de l’erreur absolue et de l’erreur relative ?
L’erreur absolue et l’erreur relative ont un large éventail d’applications dans différents domaines, notamment :
- Science – Dans des expériences scientifiques pour évaluer la précision des mesures et la qualité des résultats.
- Technologie – Fabrication et contrôle de la qualité pour évaluer la précision des machines et des équipements.
- Ingénierie – Construction et conception pour évaluer la précision des mesures et assurer la qualité des produits finis.
- Économie : évaluation des actifs et estimation des risques financiers pour évaluer l’exactitude des projections et prendre des décisions éclairées.
- Mathématiques et statistiques : modélisation et estimation pour évaluer la précision des résultats et améliorer les modèles.
Exemples pour calculer l’erreur absolue et l’erreur relative
Voici deux exemples simples pour calculer à la fois l’erreur absolue et l’erreur relative :
1. Supposons que le poids d’un objet est estimé à 3,0 kg et que son poids réel est de 2,8 kg.
Nous calculons l’erreur absolue comme suit :
Erreur absolue = Valeur réelle – Valeur estimée = 2,8 kg – 3,0 kg = -0,2 kg
Nous calculons l’erreur relative comme suit :
Erreur relative = Erreur absolue ÷ Valeur réelle = -0,2 kg ÷ 2,8 kg = -0,0714 ou -7,14 %
2. Supposons que le volume d’un conteneur est estimé à 50 litres et que son volume réel est de 45 litres.
Nous calculons l’erreur absolue comme suit :
Erreur absolue = Valeur réelle – Valeur estimée = 45 litres – 50 litres = -5 litres
Nous calculons l’erreur relative comme suit :
Erreur relative = Erreur absolue ÷ Valeur réelle = -5 litres ÷ 45 litres = -0,1111 ou -11,11 %
3. Supposons que le nombre d’habitants d’une ville est estimé à 1 million de personnes et que le nombre réel est de 975 000 personnes.
Nous calculons l’erreur absolue comme suit :
Erreur absolue = valeur réelle – valeur estimée = 975 000 – 1 000 000 = -25 000
Nous calculons l’erreur relative comme suit :
Erreur relative = Erreur absolue ÷ Valeur réelle = -25 000 ÷ 975 000 = -0,0257 ou -2,57 %
4. Supposons que la superficie d’un terrain de football soit estimée à 10 000 mètres carrés et que la superficie réelle soit de 9 900 mètres carrés.
Nous calculons l’erreur absolue comme suit :
Erreur absolue = valeur réelle – valeur estimée = 9 900 – 10 000 = -100 mètres carrés
Nous calculons l’erreur relative comme suit :
Erreur relative = Erreur absolue ÷ Valeur réelle = -100 ÷ 9 900 = -0,0101 ou -1,01 %
Dans ces exemples, l’erreur absolue et l’erreur relative nous renseignent sur la précision de l’estimation. L’erreur absolue nous indique de combien l’estimation s’est écartée de la valeur réelle, tandis que l’erreur relative nous indique de combien l’estimation s’est écartée en termes de relation avec la valeur réelle.