Une équation quadratique ou une équation quadratique est une équation de degré 2, avec laquelle le plus grand exposant de l’un de ses termes est égal à 2. Cela signifie que l’équation peut avoir jusqu’à deux solutions différentes, bien qu’elle puisse aussi avoir une solution unique ou pas du tout.
Pour calculer les solutions ou les racines des équations quadratiques, nous pouvons suivre deux procédures différentes : au moyen de la formule quadratique ou en factorisant l’expression . Dans cet article, nous parlerons des deux méthodes et nous vous donnerons quelques exercices pratiques. Bien qu’avant, nous allons clarifier certains concepts afin que toute l’explication soit très bien comprise et que vous tiriez le meilleur parti de la lecture.
Types d’équations quadratiques
La principale catégorisation entre les équations quadratiques est fonction de la structure de l’expression elle-même. Ainsi, la structure standard ou usuelle de ces expressions est la suivante : ax² + bx + c . Cette forme commune équivaut à une équation complète, mais lorsqu’il y a des termes nuls ou nuls, alors la structure peut varier, c’est là qu’apparaissent les équations incomplètes. Ensuite, nous expliquerons plus en détail les caractéristiques de tous les types.
Équations quadratiques complètes
Comme nous l’avons déjà dit, nous avons les équations quadratiques complètes , celles-ci ont tous les coefficients a, b et c différents de zéro. L’expression suit donc à la lettre la structure ax² + bx + c, puisqu’elle a tous les termes : le terme du second degré, le terme linéaire et le terme indépendant. Un exemple de ce type est l’équation suivante : x² + 2x + 1 = 0.
Équations quadratiques incomplètes
Quant aux équations incomplètes, on peut les distinguer selon quel coefficient est égal à zéro. N’oubliez pas que si cette explication ne résout pas vos doutes, juste en dessous se trouve une image dans laquelle vous pouvez trouver tous les cas expliqués étape par étape.
- Équations incomplètes (b = 0) : dans cette première situation on trouve une expression qui suit la structure suivante : ax² + c = 0. Avec laquelle, on obtient deux résultats : le négatif et le positif de la racine de la fraction c/a.
- Équations incomplètes (c = 0) : quand on a la forme ax² + bx = 0 il faut factoriser l’équation pour avoir l’expression x (ax + b) = 0. On aura donc deux solutions : x = 0 et x = -b/a.
- Equations incomplètes (b = c = 0) : dans ce cas nous avons une équation ax² = 0 et nous n’avons qu’une seule solution possible, qui est x = 0.
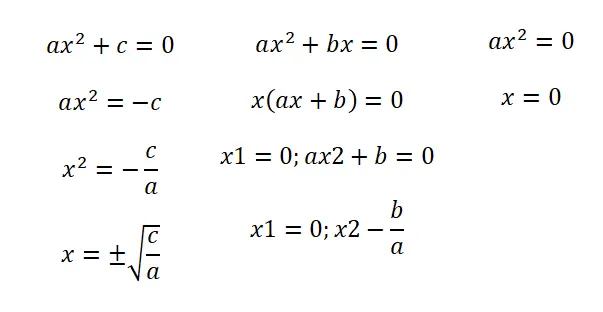
Il convient de mentionner que les procédures que nous vous avons enseignées permettent d’aller plus vite lors de la résolution d’équations incomplètes. Mais, dans tous les cas vous pouvez utiliser la formule quadratique que nous vous apprendrons plus bas, vous n’aurez qu’à écrire un zéro dans les coefficients qui n’existent pas.
Formule pour les équations quadratiques
Pour résoudre les équations quadratiques (ax² + bx + c = 0), nous devons appliquer la formule générale ou la formule quadratique, puis nous devons substituer les valeurs numériques qui correspondent à chaque lettre dans l’expression mathématique.
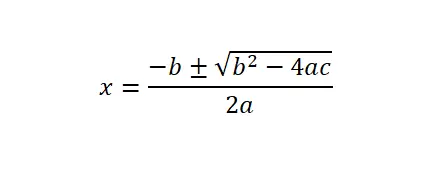
Aussi, il est important d’expliquer que le discriminant (Δ) est l’expression b² – 4ac, qui se trouve sous la racine carrée. À partir de ce concept mathématique, nous pouvons savoir combien de solutions cette équation quadratique a. Fondamentalement, il y a trois options : le discriminant est négatif (il n’y a pas de solutions réelles), le discriminant est égal à zéro (il n’y a qu’une seule solution) ou le discriminant est positif (il y a deux solutions).
Exemple d’une équation quadratique complète résolue
Essayez de résoudre l’équation quadratique suivante : 2x²+4x-6=0 et vérifiez votre résultat avec celui ci-dessous. Nous vous recommandons de suivre la procédure suivante : analyser le type d’équation (identifier les termes nuls), calculer le discriminant pour connaître le nombre de solutions existantes et enfin, résoudre l’équation proposée avec la formule.
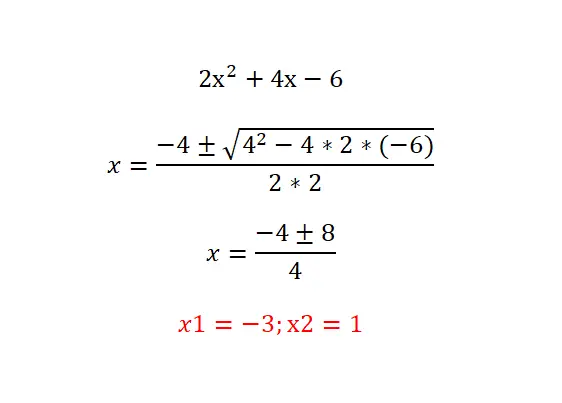
Équations quadratiques factorielles
La deuxième méthode que nous avons pour résoudre les équations quadratiques est la factorisation . Ainsi, pour factoriser un polynôme (dans notre cas un polynôme quadratique), nous pouvons utiliser différentes méthodes. Bien qu’en général, lorsqu’il s’agit d’équations de ce style, elles sont généralement factorisables par un terme commun. Et si ce n’est pas le cas, vous pouvez essayer d’appliquer les identités notables , mais normalement vous n’aurez pas besoin de connaître d’autres méthodes dans ces situations.
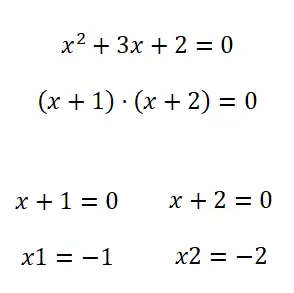
Exercices d’équations quadratiques avec solutions
Vous trouverez ci-dessous une série d’exercices sur les équations quadratiques complètes et incomplètes . De cette façon, vous passerez en revue toute la théorie expliquée tout au long de cet article et il vous sera plus clair comment l’appliquer dans les exercices. Nous vous recommandons d’essayer de les résoudre par vous-même et de ne regarder la solution que lorsque vous les avez terminées ou lorsque vous êtes bloqué. Cela dit, vous pouvez commencer à résoudre les exercices maintenant.
Exercice 1
Résolvez l’équation quadratique suivante :
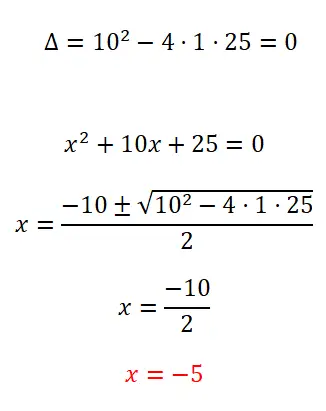
- On commence par calculer le discriminant, pour connaître le nombre de solutions possibles.
- Puisqu’il s’agit d’une équation quadratique complète, nous appliquons la formule quadratique et résolvons les calculs.
- On obtient la valeur de l’inconnu x.
Exercice 2
Résolvez l’équation quadratique suivante :
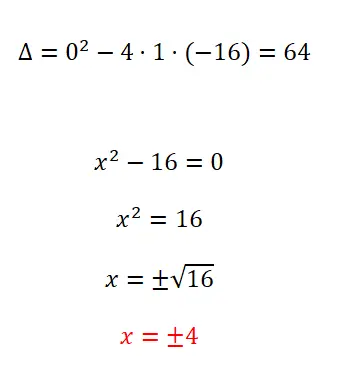
- On commence par calculer le discriminant.
- Puisque nous avons une équation quadratique incomplète dans laquelle b = 0, nous appliquons la norme pour les équations de ce type.
- Nous résolvons le calcul pour obtenir le résultat, et nous ne pouvons pas oublier le signe ±.
Exercice 3
Résolvez l’équation quadratique non ordonnée suivante :
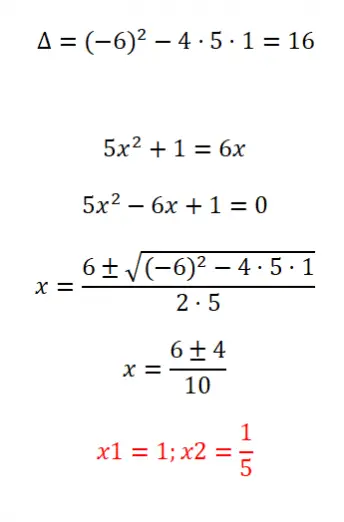
- On commence par calculer le discriminant de l’équation.
- Avant de pouvoir appliquer la formule, nous devons ordonner l’équation selon la structure ax² + bx + c = 0.
- Ensuite, nous appliquons la formule générale.
- Et enfin nous obtenons les résultats.
Exercice 4
Résolvez l’équation quadratique suivante en factorisant :
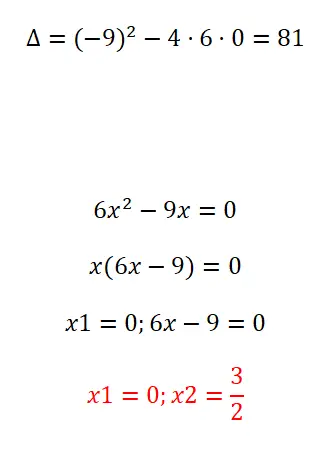
- On calcule d’abord le discriminant.
- Ensuite, nous extrayons le facteur commun de x.
- Donc la première solution est x = 0.
- Et le second est x = 3/2.
Exercice 5
Résolvez l’équation quadratique complète que nous exposons ci-dessous :
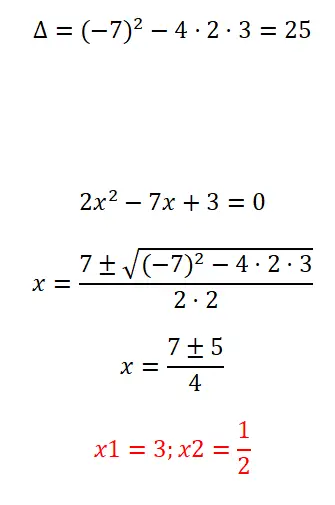
- Comme toujours, nous calculons le discriminant pour savoir combien de solutions l’équation en question a.
- Ensuite, nous appliquons la formule quadratique, puisqu’il s’agit d’une équation complète.
- Enfin, nous exprimons le résultat de l’équation.
Exercice 6
Résolvez l’équation quadratique avec des fractions que nous vous proposons :
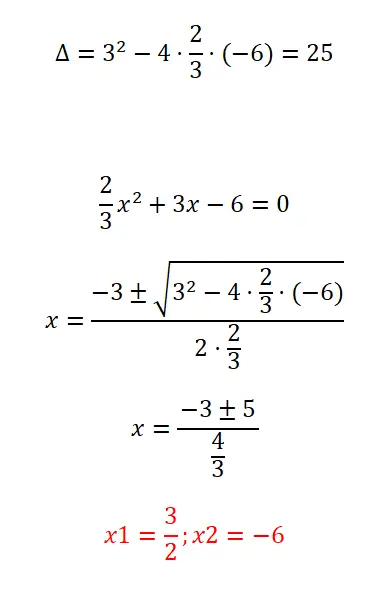
- On commence par calculer le discriminant de l’expression.
- Ensuite, nous appliquons la formule quadratique, en tenant compte du fait que le coefficient “a” est formé par une fraction.
- Nous résolvons le calcul.
- Et nous avons déjà les deux racines de l’équation.
Exercice 7
Résolvez l’équation quadratique suivante :
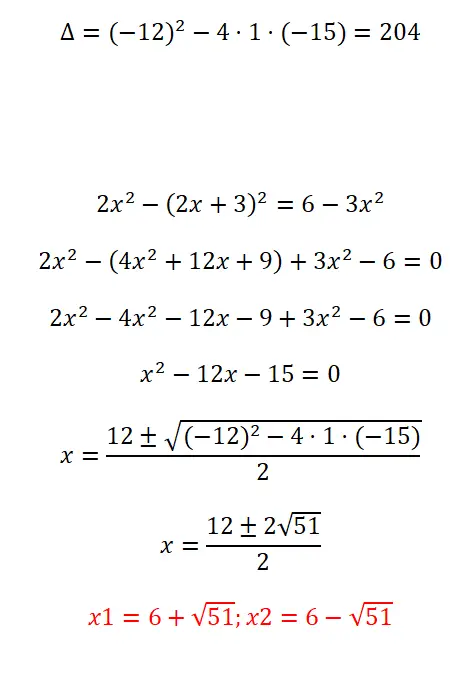
- On commence par calculer le discriminant.
- Avant d’appliquer la formule, nous devons simplifier l’expression et lui donner la forme ax² + b + c = 0.
- Nous substituons tous les coefficients de la formule et résolvons le calcul.
- Enfin, nous obtenons le résultat.
Exercice 8
Preuve de la résolution de l’équation quadratique suivante :
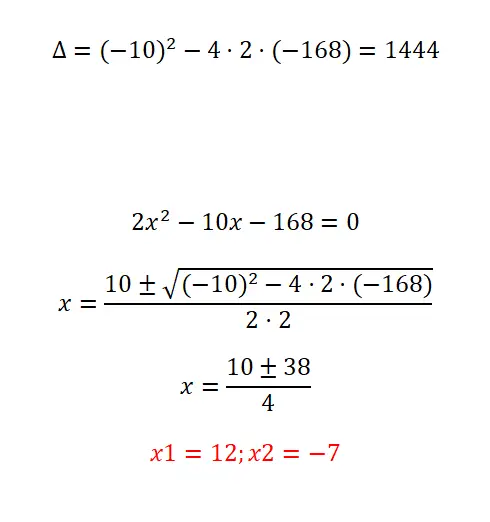
- On commence par calculer le discriminant.
- Comme vous pouvez le voir, il s’agit d’une simple équation quadratique, bien qu’elle ait des coefficients assez importants. Par conséquent, nous devons appliquer la formule et faire attention lorsque nous effectuons les opérations.
- En fin de compte, nous obtenons les deux solutions possibles.