Les équations du premier degré ou les équations linéaires sont la base de l’algèbre , car si vous ne les comprenez pas, il vous sera très difficile de comprendre des équations plus complexes. Ainsi, la particularité de ce type d’équations est que la partie littérale des monômes ne peut pas avoir d’exposant. Par conséquent, dans une équation linéaire, nous ne trouverons que des monômes sans partie littérale et des monômes avec une partie littérale sans exposant, tels que : 3 + x = -5 – 3x .
Notez également que ces équations ont généralement une solution unique, même si elles peuvent ne pas en avoir. Afin de savoir quel cas nous avons devant nous, nous devons résoudre l’équation et à la fin analyser le résultat . Ainsi, si l’on obtient une égalité impossible telle que 2 = 0, alors l’équation n’a pas de solution. D’autre part, si nous obtenons une égalité qui est toujours vraie, alors la solution est équivalente à tous les nombres réels. Et enfin, si à la fin nous obtenons l’égalité de X et une valeur numérique, dans ce cas nous aurons un résultat unique.
Procédure de résolution d’une équation linéaire
Résoudre une équation équivaut à calculer la valeur d’une variable, représentée par une lettre (x, y, a, b…). Donc, pour trouver cette valeur, nous devons suivre les étapes suivantes :
- Résolvez les parenthèses et les fractions : pour commencer, nous supprimons toutes les parenthèses et les dénominateurs, afin d’obtenir une équation plus facile à comprendre. Parce que nous pouvons apprécier directement quels termes sont accompagnés de l’inconnu et lesquels ne le sont pas, cette lecture nous permet de poursuivre facilement la résolution de l’expression.
- Simplifions l’expression : on regroupe les termes semblables, (les termes indépendants d’une part, et les termes avec x d’autre part). Ainsi, d’un côté on laissera les nombres qui ont l’inconnue et on passera les autres nombres du côté opposé. Mais rappelez-vous que pour changer leurs côtés, nous devons changer leur signe.
- Opérer de chaque côté : nous effectuons toutes les opérations dans l’ordre suivant : puissances/racines, multiplications/divisions et additions/soustractions. Nous faisons cela jusqu’à ce que nous obtenions un seul terme de chaque côté, et donc nous nous retrouvons avec une équation avec la même structure que celle-ci : 4x = 8.
- Isoler la variable : enfin, il suffit de passer la valeur qui accompagne la lettre en divisant de l’autre côté et on trouve ainsi sa valeur finale. A la fin de cette étape nous aurons résolu l’inconnue et nous saurons quel type de résultat nous reste : une solution unique, une solution invalide ou une solution qui se satisfait de tous les entiers.
Exemples d’équations du premier degré
Ci-dessous, vous trouverez des équations du premier degré résolues , qui sont organisées en différentes catégories selon la complexité de leur structure. Ainsi, connaissant la procédure théorique pour résoudre les équations linéaires et les différents types qui existent, vous aurez déjà les connaissances nécessaires pour pouvoir les résoudre facilement et nous commencerons par la pratique. Cela dit, commençons par l’explication théorique :
Équations de base du premier degré
Ce premier type d’équations linéaires n’est composé que des opérations arithmétiques de base (addition, soustraction, multiplication et division). Voici deux exemples travaillés, le premier est un peu plus basique et le second est un peu plus complexe en terme de calcul :
-6x + 4 – 1 = 6x -3
-6x + 3 = 6x – 3
-6x – 6x = -3 – 3
-12x = -6
x = 1 / 2
-24x – 3 + 4x = -4x – 27
-20x – 3 = -4x – 27
-20x + 4x = -27 + 3
-16x = -24
x = 3 / 2
Équations du premier degré avec parenthèses
Deuxièmement, nous avons les équations linéaires entre parenthèses. Celles-ci sont un peu plus compliquées à résoudre que les précédentes, bien que leur seule difficulté réside dans le calcul, puisqu’il faut respecter les propriétés des parenthèses. Pour que ce soit plus clair, nous vous montrons deux exemples travaillés :
2(x + 3) – 4x = -4
2x + 6 – 4x = -4
-2x = -10
x = 5
-2 + 3 (4x + 5) = -1 (x + 2) + 2 (-3x + 2)
-2 + 12x + 15 = -x – 2 – 6x + 4
13 + 12x = -7x + 2
12x + 7x = -13 + 2
19x = -11
x = -11 / 19
Équations du premier degré avec puissances et racines
Le troisième niveau est assez simple, puisqu’il ne fait qu’ajouter des pouvoirs et des racines. La seule difficulté que vous pouvez rencontrer avec ces équations est lorsque l’exposant ou la racine affecte une parenthèse entière (comme le deuxième exemple que nous allons vous montrer), mais tout le reste reste à peu près le même. Vous trouverez ci-dessous deux exemples.
3² + √25 – 2x = 2³x + 4
9 + 5 – 2x = 8x + 4
14 – 2x = 8x + 4
-2x – 8x = -14 + 4
-10x = -10
x = 1
4x + (2 – 1 +5)² = 3x – √16
4x + 6² = 3x – 4
4x – 3x = -4 -36
x = -40
Équations du premier degré avec des fractions
La dernière catégorie d’équations linéaires que nous pouvons trouver est celle-ci, qui est composée de tous les éléments que nous avons commentés précédemment et aussi, par fractions. Ce niveau est le plus complexe et il existe plusieurs méthodes pour les résoudre. La première et la plus simple consiste à multiplier les dénominateurs par le côté opposé de l’égalité, bien que nous ne puissions l’utiliser que lorsque nous avons deux fractions. D’autre part, si nous avons plus de deux fractions dans l’équation, nous devons trouver un dénominateur commun et multiplier toutes les fractions en divisant cette valeur par le dénominateur de la même fraction. Vous trouverez ci-dessous un exemple de chaque type :
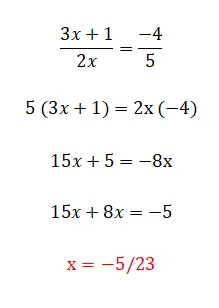
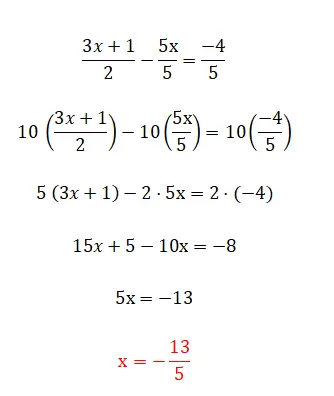
Exercices sur les équations du premier degré
Maintenant, nous proposons quelques exercices d’équations linéaires. Elles sont organisées selon une difficulté croissante, avec laquelle les premières équations sont plus faciles que les dernières. Par conséquent, nous vous recommandons de commencer par le début et de voir jusqu’où vous pouvez aller. Alors, essayez de résoudre les équations suivantes, puis comparez votre résultat avec les solutions que nous proposons.
Premier exercice
Le premier exercice est une équation linéaire très simple, puisqu’elle n’est composée que d’additions et de soustractions, et elle n’a également que quatre termes entre les deux côtés de l’égalité :
2x – 3 = 4x + 5
2x – 4x = 5 + 3
-2x = 8
x = 8 / (-2)
x = -4
- Nous regroupons des termes similaires.
- Nous simplifions les deux côtés.
- Nous effaçons l’inconnu et calculons sa valeur.
deuxième exercice
Dans ce cas, nous nous retrouvons avec une équation formée par des parenthèses, avec laquelle notre priorité absolue est de les éliminer, afin de pouvoir ensuite regrouper les termes similaires :
-4(x + 2) + 5x = 6 + 5x
-4x – 8 + 5x = 6 + 5x
-4x + 5x – 5x = 6 + 8
-4x = 14
x = 14 / (-4) = -7 / 2
- Nous résolvons les parenthèses.
- Nous déplaçons les x vers la gauche et les termes indépendants vers la droite.
- Nous clarifions l’inconnu.
Nous simplifions le résultat.
troisième exercice
Ensuite, vous devrez résoudre une autre équation du premier degré avec des parenthèses, bien que celle-ci soit un peu plus difficile. C’est parce qu’il a des parenthèses imbriquées (des parenthèses à l’intérieur d’autres). Par conséquent, vous devez suivre correctement l’ordre de résolution : d’abord les initiés puis les étrangers.
3x + 2 (x – (4x – 5)) = 1 – (3 (2x + 7) – 2)
3x + 2 (x – 4x + 5) = 1 – (6x + 21 – 2)
3x + 2x – 8x + 10 = 1 – 6x – 21 + 2
-3x + 10 = -6x – 18
3x = -28
x = -28 / 3
- Nous commençons par résoudre les parenthèses intérieures.
- Ensuite, nous résolvons les parenthèses extérieures.
- Nous simplifions les deux côtés de l’égalité et collectons des termes similaires.
- Nous isolons x et calculons sa valeur.
quatrième exercice
Dans cet exercice, nous commençons à voir les fractions, qui sont probablement l’élément le plus compliqué des équations linéaires. Bien que ne vous inquiétez pas car si vous avez lu la théorie, vous saurez parfaitement comment procéder :
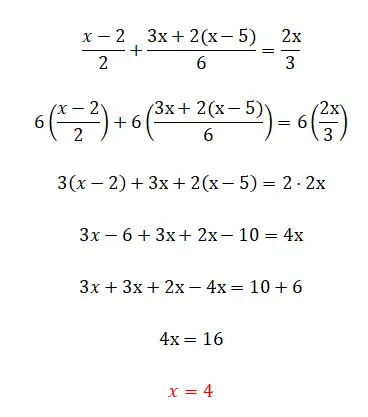
Cinquième exercice
Dans ce cinquième exercice, nous voyons des fractions entre parenthèses, ce qui signifie que la hiérarchie de résolution devient un peu compliquée. Il convient de mentionner que cet exemple peut être résolu au moyen de deux méthodes : en utilisant la méthode des plus petits communs multiples ou en opérant directement avec les fractions. Ci-dessous, vous pouvez voir les deux procédures complètes :
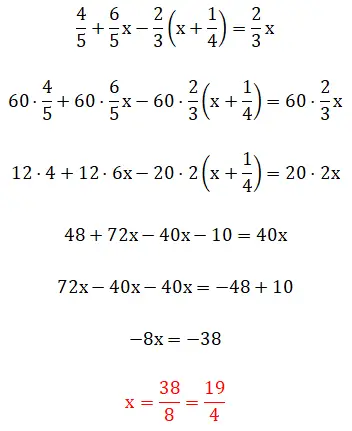
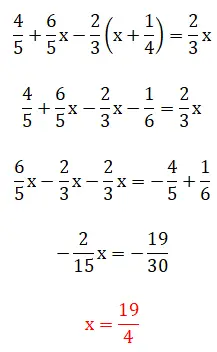
sixième exercice
Ensuite, nous allons un peu plus loin avec le sujet des fractions et des parenthèses, puisque nous avons des parenthèses imbriquées. Cet exercice n’apporte pas beaucoup plus de complications par rapport au précédent, il est simplement un peu plus difficile au niveau des calculs et c’est tout.
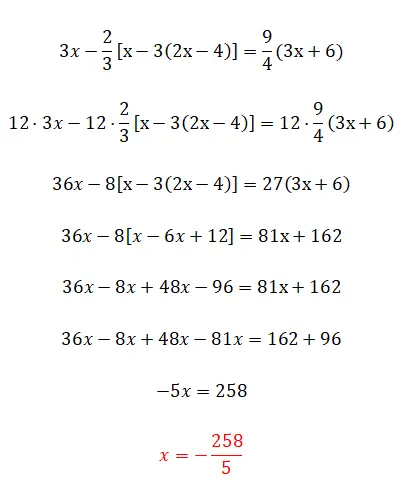
- Nous multiplions tous les termes par le ppcm des dénominateurs.
- Nous simplifions l’expression en supprimant les parenthèses : d’abord celles à l’intérieur puis celles à l’extérieur.
- Nous regroupons les termes similaires de chaque côté.
- Nous résolvons les opérations de chaque côté.
- Et nous calculons la valeur de l’inconnu.
septième exercice
L’exercice suivant peut sembler très facile, mais nous vous recommandons d’essayer de le résoudre quand même, car il vous donnera sûrement un résultat un peu particulier. Après l’avoir essayé, regardez la solution et l’explication sous l’exercice.
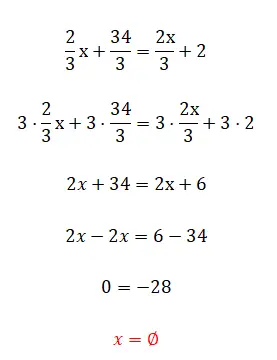
- Nous multiplions toutes les fractions avec le lcm des dénominateurs.
- On simplifie l’expression obtenue.
- Et enfin nous voyons qu’il nous donne une fausse égalité, puisque nous avons éliminé l’inconnu.
Comme vous l’avez peut-être remarqué, il s’agit d’une fausse égalité ou d’une égalité sans résultat, puisqu’il n’y a pas de valeur qui complète correctement l’équation. C’est l’un des cas que nous avons évoqués dans l’introduction.
huitième exercice
Enfin, nous vous proposons cet exercice qui est assez compliqué car il comporte toutes les complications que nous avons vues tout au long de cet article, bien qu’il ait aussi une petite astuce. Commentez que si vous êtes capable de résoudre cette équation du premier degré, alors vous avez parfaitement compris toute la théorie. Et si ce n’est pas le cas, ne vous inquiétez pas, car cet exercice est assez compliqué.
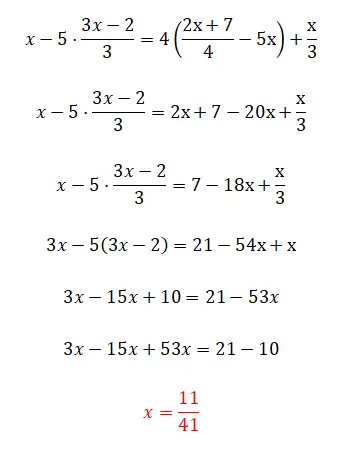
- Nous commençons par éliminer les quatre du côté droit de l’équation.
- Ensuite, nous joignons les x sur le côté droit.
- On multiplie par trois tous les termes, afin d’éliminer les dénominateurs.
- Nous supprimons les parenthèses.
- Nous assemblons des termes similaires.
- On calcule la valeur de l’inconnu.
Plus d’exercices d’équations linéaires
Maintenant que vous vous êtes suffisamment entraîné, vous devriez être capable de résoudre des équations linéaires complexes . Bien que si vous souhaitez continuer à pratiquer, nous vous recommandons d’essayer de résoudre cette feuille d’exercices . Mais si vous pensez en avoir assez parcouru, nous pouvons aussi vous proposer un article qui pourra vous aider à comprendre la hiérarchie des opérations . De cette façon, vous saurez quel calcul résoudre en premier à tout moment et vous ne vous tromperez jamais .