Sur cette page vous trouverez les formules de toutes les équations du plan et comment elles sont calculées. Vous découvrirez également comment trouver l’équation de n’importe quel plan avec son vecteur normal. De plus, vous pourrez voir des exemples et pratiquer avec des exercices résolus des équations du plan.
Quelle est l’équation du plan ?
En géométrie analytique, l’ équation d’un plan est une équation qui permet d’exprimer mathématiquement n’importe quel plan. Donc, pour trouver l’équation d’un plan, vous n’avez besoin que d’un point et de deux vecteurs linéairement indépendants appartenant à ce plan.
Avant de poursuivre l’explication des équations du plan, il est essentiel que vous compreniez ce qu’est le plan (géométrie) , car sinon il y aura des choses que vous ne comprendrez pas. Si vous n’êtes pas tout à fait clair, vous pouvez le consulter sur ce lien, où nous avons concentré tout ce que vous devez savoir sur le plan.
Quelles sont les équations du plan ?
Comme nous l’avons vu dans la définition de l’équation d’un plan, tout point d’un plan plat peut être exprimé comme une combinaison linéaire de 1 point et de 2 vecteurs.

Cependant, une condition nécessaire pour que l’équation corresponde à un plan est que les deux vecteurs du plan aient une indépendance linéaire, c’est-à-dire que les deux vecteurs ne puissent pas être parallèles l’un à l’autre.
Ainsi, tous les types d’équations du plan sont : l’ équation vectorielle , les équations paramétriques , l’ équation implicite (ou générale) et l’ équation canonique (ou segmentaire) du plan.
Ensuite nous allons voir en détail l’explication et la formule de toutes les équations du plan.
Équation vectorielle du plan
Soit un point et deux vecteurs directeurs d’un plan :
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
La formule de l’équation vectorielle d’un plan est :
![]()
Ou équivalent:
![]()
Où
![]() et
et![]() sont deux scalaires, c’est-à-dire deux nombres réels.
sont deux scalaires, c’est-à-dire deux nombres réels.
Équations paramétriques du plan
L’équation paramétrique d’un plan peut être déterminée à partir de son équation vectorielle. Ci-dessous, vous pouvez voir la démo.
Soit l’équation vectorielle de n’importe quel plan :
![]()
Nous opérons et effectuons d’abord les produits de vecteurs par les scalaires :
![]()
Ensuite, nous ajoutons les composants :
![]()
Et, enfin, nous obtenons les équations paramétriques du plan en assimilant les coordonnées correspondant à chaque variable séparément :
![]()
Où:
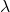 et
et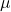 sont deux scalaires, c’est-à-dire deux nombres réels.
sont deux scalaires, c’est-à-dire deux nombres réels.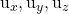 sont les composantes de l’un des deux vecteurs directeurs du plan
sont les composantes de l’un des deux vecteurs directeurs du plan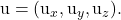
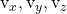 sont les composantes de l’autre vecteur directeur du plan
sont les composantes de l’autre vecteur directeur du plan 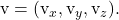
Équation implicite ou générale du plan
Soit un point et deux vecteurs directeurs d’un plan :
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
L’équation implicite, générale ou cartésienne d’un plan s’obtient en résolvant le déterminant suivant et en fixant le résultat égal à 0 :
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-68d67612dfa54d76666aa37b702a472f_l3.png)
Ainsi, l’ équation implicite ou générale du plan résultant sera la suivante :
![]()
Ce type d’équation du plan est aussi appelé équation cartésienne du plan.
Équation canonique ou segmentaire du plan
La formule de l’équation canonique ou segmentaire d’un plan est la suivante :
![]()
Où:
 est le point d’intersection entre le plan et l’axe X.
est le point d’intersection entre le plan et l’axe X. est le point d’intersection entre le plan et l’axe Y.
est le point d’intersection entre le plan et l’axe Y. C’est là que le plan coupe l’axe Z.
C’est là que le plan coupe l’axe Z.
L’équation canonique (ou équation segmentaire) du plan peut également être obtenue à partir de son équation générale :
![]()
Tout d’abord, nous résolvons le coefficient D de l’équation :
![]()
Puis on divise l’équation entière du plan par la valeur du paramètre D changé de signe :
![]()
![]()
Et, en utilisant les propriétés des fractions, nous arrivons à l’expression suivante :
![]()
On déduit donc de cette expression les formules permettant de calculer directement les termes de l’équation canonique ou segmentaire d’un plan :
![]()
Par conséquent, pour pouvoir former cette variante des équations du plan, il faut que les coefficients A, B et C soient différents de zéro, évitant ainsi les indéterminations des fractions.
Comment calculer l’équation d’un plan à partir de son vecteur normal
Un problème très typique des équations d’un plan est de trouver à quoi ressemble l’équation d’un plan donné à partir d’un point et de son vecteur normal (ou perpendiculaire). Alors, voyons comment ça marche.
Mais il faut d’abord savoir que les composantes X, Y, Z du vecteur normal à un plan coïncident respectivement avec les coefficients A, B, C de l’équation implicite (ou générale) dudit plan.
![]()
Où
![]() est le vecteur orthogonal au plan
est le vecteur orthogonal au plan![]()
Une fois que nous connaissons la relation précédente, voyons un exemple de résolution de ce type de problèmes d’équations planes :
- Déterminer l’équation implicite ou générale du plan qui passe par le point
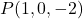 et l’un de ses vecteurs normaux est
et l’un de ses vecteurs normaux est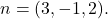
La formule de l’équation implicite, générale ou cartésienne d’un plan est :
![]()
Ainsi, à partir du vecteur normal, on peut trouver les coefficients A, B et C car ils sont équivalents aux composantes de son vecteur normal :
![]()
Alors que nous n’avons qu’à trouver le paramètre D. Pour ce faire, nous substituons les coordonnées du point qui appartient au plan dans l’équation :
![]()
![]()
![]()
![]()
![]()
Donc l’équation implicite ou générale du plan est :
![]()
Problèmes résolus de l’équation du plan
Exercice 1
Déterminer l’équation vectorielle du plan qui contient le vecteur
![]() et passe par les deux points suivants :
et passe par les deux points suivants :![]() et
et ![]()
Pour connaître l’équation d’un plan, il faut un point et deux vecteurs et dans ce cas nous n’avons qu’un seul vecteur, il faut donc trouver un autre vecteur directeur du plan. Pour cela, on peut calculer le vecteur qui définit les deux points du plan :
![]()
Maintenant que nous connaissons déjà deux vecteurs directeurs du plan et un point, nous utilisons donc la formule de l’équation vectorielle du plan :
![]()
Et nous substituons les deux vecteurs et l’un des deux points du plan dans l’équation :
![]()
Exercice 2
Trouvez les équations paramétriques du plan qui contient les trois points suivants :
![]()
Pour trouver les équations paramétriques du plan, nous devons trouver deux vecteurs linéairement indépendants qui se trouvent dans le plan. Et, pour cela, on peut calculer deux vecteurs qui sont définis par les 3 points :
![]()
![]()
Les coordonnées des deux vecteurs trouvés ne sont pas proportionnelles, elles sont donc linéairement indépendantes l’une de l’autre.
Maintenant que nous connaissons déjà deux vecteurs directeurs et un point du plan, nous appliquons donc la formule de l’équation paramétrique du plan :
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f5adabb85c9285653d6b638f7c48ba50_l3.png)
Et nous substituons les deux vecteurs et l’un des trois points du plan dans l’équation :
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=4 + \lambda \cdot (-2)+ \mu \cdot (-3) \\[1.7ex] y=1 + \lambda \cdot (-4) + \mu \cdot 4 \\[1.7ex] z=0 + \lambda\cdot (-1) + \mu \cdot 3 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f57edaf8a85108cffb796470ffca8484_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}\bm{x=4 -2 \lambda-3\mu } \\[1.7ex] \bm{y=1-4 \lambda+4 \mu } \\[1.7ex] \bm{z=-\lambda + 3\mu } \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4cab5ddc074bd7df6849d71854207cf5_l3.png)
Exercice 3
Trouver l’équation implicite ou générale du plan qui passe par le point
![]() et contient les vecteurs
et contient les vecteurs![]() et
et ![]()
Pour calculer l’équation générale ou implicite du plan, il faut résoudre le déterminant suivant formé par les deux vecteurs, les trois variables et les coordonnées du point :
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-917f1770ff2a17897e5df76998ec3519_l3.png)
Donc, nous substituons les vecteurs et le point dans la formule :
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}4 & 5 & x+2 \\[1.1ex]1 & 3 & y-1 \\[1.1ex]3& 1 & z+1 \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-02e103601cd9992a8a8c087d016a08c1_l3.png)
Et maintenant on résout le déterminant de la matrice 3×3 avec la méthode de votre choix :
![]()
Enfin, nous effectuons les opérations et regroupons les termes similaires :
![]()
![]()
![]()
Donc l’équation implicite ou générale du plan est :
![]()
Exercice 4
Déterminez si le point
![]() appartient au plan suivant :
appartient au plan suivant :
![]()
Pour que le point soit dans le plan, il faut vérifier son équation. Par conséquent, nous devons substituer les coordonnées cartésiennes du point dans l’équation du plan et vérifier si l’équation est remplie :
![]()
![]()
![]()
![]()
![]()
Le point ne respecte pas l’équation du plan, il ne fait donc pas partie de ce plan.
Exercice 5
Trouver l’équation segmentaire du plan dont l’équation générale (ou implicite) est :
![]()
Tout d’abord, nous effaçons le terme indépendant de l’équation :
![]()
Puis on divise l’équation entière du plan par la valeur du coefficient D changé de signe :
![]()
![]()
Et, en utilisant les propriétés des fractions, nous arrivons à l’expression suivante :
![]()
Donc l’équation segmentaire (ou canonique) du plan est :
![]()
Exercice 6
Calcule l’équation implicite ou générale du plan dans l’espace qui passe par le point
![]() et l’un de ses vecteurs normaux est
et l’un de ses vecteurs normaux est ![]()
La formule de l’équation implicite, générale ou cartésienne d’un plan est :
![]()
Eh bien, à partir du vecteur normal, nous pouvons trouver les coefficients A, B et C, car ils sont respectivement égaux aux composantes du vecteur normal :
![]()
Pour que nous ayons seulement besoin de trouver le paramètre D. Pour ce faire, nous substituons les coordonnées du point qui appartient au plan dans l’équation :
![]()
![]()
![]()
![]()
![]()
En conclusion, l’équation implicite ou générale du plan est :
![]()
Exercice 7
Trouver les équations paramétriques du plan qui contient la droite
![]() et est parallèle à la droite
et est parallèle à la droite![]() étant les lignes :
étant les lignes :
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=1+t \\[1.7ex] y=2-3t\\[1.7ex] z=4+2t \end{cases} \qquad \qquad s: \ \frac{x-4}{2} = \frac{y+3}{2}= \frac{z-2}{-3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-624f315685b292c4bb05e9cb4b931a97_l3.png)
Pour trouver les équations paramétriques du plan, nous avons besoin de connaître deux vecteurs directeurs et un point dudit plan. La déclaration nous dit qu’elle contient la ligne
![]() Par conséquent, nous pouvons prendre le vecteur directeur et un point sur cette ligne pour définir le plan. De plus, l’énoncé nous dit que le plan est parallèle à la droite
Par conséquent, nous pouvons prendre le vecteur directeur et un point sur cette ligne pour définir le plan. De plus, l’énoncé nous dit que le plan est parallèle à la droite![]() nous pouvons donc également utiliser le vecteur directeur de cette ligne pour l’équation du plan.
nous pouvons donc également utiliser le vecteur directeur de cette ligne pour l’équation du plan.
le droit
![]() s’exprime sous la forme d’équations paramétriques, donc les composantes de son vecteur directeur sont les coefficients des termes de paramètre
s’exprime sous la forme d’équations paramétriques, donc les composantes de son vecteur directeur sont les coefficients des termes de paramètre ![]()
![]()
Et les coordonnées cartésiennes d’un point sur cette même ligne sont les termes indépendants des équations paramétriques :
![]()
D’autre part, la ligne droite
![]() est sous la forme d’une équation continue, telle que les composantes de son vecteur directeur soient les dénominateurs des fractions :
est sous la forme d’une équation continue, telle que les composantes de son vecteur directeur soient les dénominateurs des fractions :
![]()
Par conséquent, les équations paramétriques du plan sont :
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f5adabb85c9285653d6b638f7c48ba50_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=1 + \lambda \cdot 1+ \mu \cdot 2 \\[1.7ex] y=2 + \lambda \cdot (-3) + \mu \cdot 2 \\[1.7ex] z=4 + \lambda\cdot 2 + \mu \cdot (-3) \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c81f4d8e5aa907f111b3389d5137736e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}\bm{x=1 + \lambda+2\mu } \\[1.7ex] \bm{y=2-3 \lambda+2 \mu } \\[1.7ex] \bm{z=4+2\lambda -3\mu } \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fccd86ac9a3e4084e324d8e5b1071e59_l3.png)